An Informal Introduction to Formal Languages
© 2019 Brian Heinold
Licensed under a Creative Commons Attribution-Noncommercial-Share Alike 4.0 Unported License
Here is a pdf version of the book.
Preface
There are notes I wrote for my Theory of Computation class in 2018. This was my first time teaching the class, and a lot of the material was new to me. Trying to learn the material from textbooks, I found that they were often light on examples and heavy on proofs. These notes are meant to be the opposite of that. There are a lot of examples, and no formal proofs, though I try to give the intuitive ideas behind things. Readers can consult any of the standard textbooks for formal proofs.
If you spot any errors, please send me a note at heinold@msmary.edu.
Strings and Languages
Strings
An alphabet is a set of symbols. We will use the capital Greek letter Σ (sigma) to denote an alphabet. Usually the alphabet will be something simple like Σ = {0,1} or Σ = {a,b,c}.
A string is a finite sequence of symbols from an alphabet. For instance, ab, aaaaa, and abacca are all strings from the alphabet Σ = {a,b,c}.
String operations and notation
- The concatenation of strings u and v, denoted uv, consists of the symbols of u followed by the symbols of v. For instance, if u = 100 and v = 1111, then uv = 1001111.
- The notation un stands for u concatenated with itself n times. For instance, u2 is uu and u3 is uuu. So if u = 10, then u2 = 1010 and u3 = 101010. Note that u0 is the empty string.
- The notation uR stands for the reverse of u. For instance, if u is 00011, then uR is 11000.
- The length of u is denoted |u|. For instance, if u = 10101010, then |u| = 8.
- The empty string is the string with length 0. It is denoted by the Greek letter λ (lambda). Another common notation for it is ε (epsilon).
- Given an alphabet Σ, the notation Σ* denotes the set of all possible strings from Σ. For instance, if Σ = {a,b}, then Σ* = {λ, a, b, aa, ab, ba, bb, aaa, aab, …}.
Languages
Given an alphabet Σ, a language is a subset of strings built from that alphabet. Here are a few example languages from Σ = {a,b}:
- {a,aa,b,bb} — Any subset of strings from Σ*, such as this subset of four items, is a language.
- {abn : n ≥ 1} — This language consists of ab, abb, abbb, etc. In particular it's all strings consisting of an a followed by at least one b,
- {anbn : n ≥ 0} — This is all strings that start with some number of a's followed by the same number of b's. In particular, it is λ, ab, aabb, aaabbb, etc.
Operations on languages
Since languages are sets, set operations can be applied to them. For instance, if L and M are languages, we can talk about the union L ∪ M, intersection L ∩ M, and complement L.
Another important operation on two languages L and M is the concatenation LM, which consists of all the strings from L with all the strings from M concatenated to the end of them. The notation Ln is used just like with strings to denote L concatenated with itself n times.
One final operation is called the Kleene star operation. Given a language L, L* is all strings that can be created from concatenating together strings from L. Formally, it is L0 ∪ L1 ∪ L2 ∪ …. Informally, think of it as all the strings you can create by putting together strings of L with repeats allowed.
Here are some examples. Assume Σ = {a,b},
- Let L = {a, ab, aa} and M = {a, bb}. Then L ∪ M = {a, ab, aa, bb} and L ∩ M = {a}.
- Let L = {λ, a, b}. Then L consists of any string from Σ* except the three things in L. In particular, it is any string of a's and b's with length at least 2.
- Let L = {b, bb} and M = {an : n ≥ 1}. Note that M is all strings of one or more a's. Then the concatenation LM is {ba, bba, baa, bbaa, baaa, bbaaa, baaaa, bbaaaa, …}.
- Let L = {aa, bbb}. Then some things in L* are aa, aabbb, aabbbaa, and bbbbbbaaaa. In general, L* contains anything we can get by concatenating the strings from L in any order, with repeats allowed. Note that λ is always in L*.
Automata
Introduction
Here is an example of something called a state diagram.

It depicts a hypothetical math minor at a college. P and F stand for pass and fail. The four circles are the possible states you can be in. The arrow pointing to the Calc 1 state indicates that you start at that state. The other arrows indicate which class you move to depending on whether you pass or fail the current class. The state with the double circle is called an accepting state. A student only completes a minor if they get to that accepting state.
We can think of feeding this machine a string of P's and F's, like PPFP, and seeing what state we end up in. For this example, we start at Calc 1, get a P and move to Calc 2, then get another P and move to Calc 3, then get an F and stay at Calc 3, and finally get a P to move to the Done state. This string is considered to be accepted. A different string, like FFPF would not be considered accepted because we would end up in the Calc 2 state, which is not an accepting state.
Deterministic Finite Automata
State diagrams like the example above are used all over computer science and elsewhere. We will be looking at a particular type of state diagram called a Deterministic Finite Automaton (DFA). Here is an example DFA:

We feed this DFA input strings of 0s and 1s, follow the arrows, and see if we end up in an accepting state (q1) or not (q0 or q2). For instance, suppose we input the string 001100. We start at state q0 (indicated by the arrow from nowhere pointing into it). With the first 0 we follow the 0 arrow from q0 looping back to itself. We do the same for the second 0. Now we come to the third symbol of the input string, 1, and we move to state q1. We then loop back onto q1 with the next 1. The fifth symbol, 0, moves us to q2, and the last symbol, 0, moves us back to q1. We have reached the end of the input string, and we find ourselves in q1, an accepting state, so the string 001100 is accepted.
On the other hand, if we feed it the string 0111000, we would trace through the states q0 → 0 q0 → 1 q1 → 1 q1 → 1 q1 → 0 q2 → 0 q1 → 0 q2, ending at a non-accepting state, so the string is not accepted.
With a little thought, one can work out that the strings that are accepted by this automaton are those start with some number of 0s (possibly none), followed by a single 1, and then after that are followed by some (possibly empty) string of 0s and 1s that has an even number of 0s.
Formal Definition and Details
The word automaton (plural automata) refers in typical English usage to a machine that runs on its own. In particular, we can think of a DFA as a machine that we feed a string into and get an output of “accepted” or “not accepted”. A DFA is in essence a very simple computer. One of our main goals is to see just how powerful this simple computer is—in particular what things it can and can't compute.The deterministic part of the name refers to the fact that a given input string will always lead to the same path through the string. There is no choice or randomness possible. The same input always gives the exact same sequence of states.
We will mostly be drawing DFAs like in the figures shown earlier, but it's nice to have a formal definition to clear up any potential ambiguities. You can skip this part for now if you think you have a good handle on what a DFA is, but you may want to come back to it later, as formal definitions are useful especially for answering questions you might have (such as if a DFA can have an infinite number of states or if it can have multiple start states).
A DFA is given by five values (Q, Σ, δ, q0, F) with the following definitions:
- Q is a finite set of objects called states
- Σ is a finite alphabet
- δ (delta) is a function δ: Q × Σ → Q that specifies all the transitions from state to state.
- q0 ∈ Q is a particular state called the start or initial state.
- F ⊆ Q is a collection of states that are the final or accepting states.
In short, a DFA is defined as a collection of states with transitions between them along with a single initial state and zero or more accepting states. The definition, though, brings up several important points:
- Q is a finite set. So there can't be an infinite number of states.
- Σ is any finite alphabet. For simplicity, we will almost always use Σ = {0,1}.
- The trickiest part of the definition is probably δ, the function specifying the transitions. A transition from state q0 to q1 via a 1 would be δ(q0,1) = q1. With this definition, we can represent a DFA without a diagram. We could simply specify transitions using function notation or in a table of function values.
- Every state must have a transition for every symbol of the alphabet. We can't leave any possibility undone.
- There can be only one initial state.
- Final states are defined as a subset of the set of states. In particular, any amount of the states can be final, including none at all (the empty set).
- A DFA operates by giving it an input string. It then reads the string's symbols one-by-one from left to right, applying the transition rules and changing the state accordingly. The string is considered accepted if the machine is in an accepting state after all the symbols are read.
- The language accepted by a DFA is the set of all input strings that it accepts.
Finally, note that in some books and references you may see DFAs referred to as deterministic finite accepters or as finite state machines.
Examples
Here are a number of examples where we are given a language and want to build a DFA that accepts all the strings in that language and no others. Doing this can take some thought and creativity. There is no general algorithm that we can use. One bit of advice is that it often helps to create the states first and fill in the transitions later. It also sometimes helps to give the states descriptive names.
For all of these, assume that the strings come from the alphabet Σ = {0,1}, unless otherwise mentioned. Below are all the examples we will cover in case you want to try them before looking at the answers.
- All strings ending in 1.
- All strings with an odd number of 1s.
- All strings with at least two 0s.
- All strings with at most two 0s.
- All strings that start with 01.
- All strings of the form 0n1 with n ≥ 0 (this is all strings that start with any number of 0s (including none) followed by a single 1).
- All strings of the form 0101n with n ≥ 0.
- All strings in which every 1 is followed by at least two 0s.
- All strings that end with the same symbol they start with.
- All strings whose length is a multiple of 3.
- All strings with an even number of 0s and an even number of 1s.
- All strings of 0s and 1s.
- All nonempty strings of 0s and 1s.
- Only the string 001.
- Any string except 001.
- Only the strings 01, 010, and 111.
- All strings that end in 00 or 01.
- All strings with at least three 0s and at least two 1s.
- All strings containing the substring 11001.
Here are the solutions.
- All strings ending in 1.

We have two states here, q0 and q1. Think of q0 as being the state we're in if the last symbol we've seen is not a 1, and q1 as being the state we're in if the last symbol we've seen is a 1. If we get a 0 at q0, we still don't end in 1, so we stay at q0, but if we get a 1, then we do now end in 1, so we move to q1. From q1, things are revered: a 1 should keep us at q1, but a 0 means we don't end in 1 anymore and we should therefore move back to q0.
- All strings with an odd number of 1s.

Here we have named the states E for an even number of 1s and O for an odd number. As we move through the input string, if we have seen an even number of 1s so far, then we will be in State E, and otherwise we will be in State O. A 0 won't change the number of 1s, so we stay at the current state whenever we get a 0. A 1 does change the number of 1s, so we flip to the opposite state whenever we get a 1.
- All strings with at least two 0s.

The states are named 0, 1, and 2 to indicate how many 0s we have seen. Each new 0 moves us to the next state, and a 1 keeps us where we are. Once we get to State 2, we have reached our goal of two 0s, and nothing further in the input string can change that fact, so we loop with 0 and 1 at State 2.
- All strings with at most two 0s.

This is very similar to the previous example. One key difference is we want at most two 0s, so the accepting states are now States 0, 1, and 2. State 3, for three or more 0s, is an example of a junk state (though most people call it a trap state or a dead state). Once we get into a junk state, there is no escape and no way to be accepted. We will use junk states quite a bit in the DFAs we create here.
- All strings that start with 01.
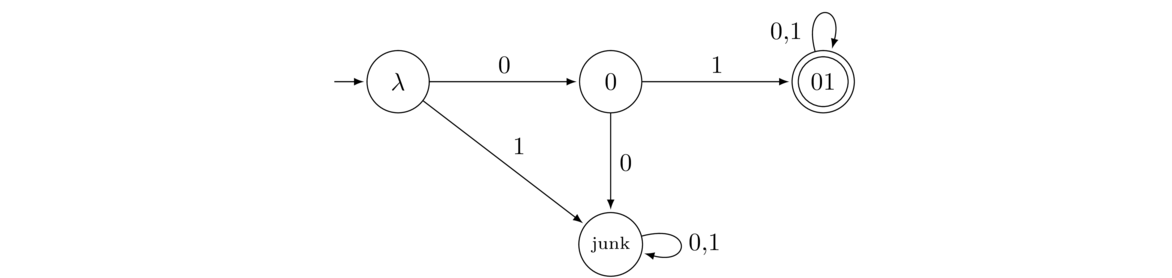
Here our states are named λ, 0, and 01, with an explicit junk state. The first three states record our progress towards starting with 01. Initially we haven't seen any symbols, and we are in State λ. If we get a 0 we move to State 0, but if we get a 1, then there's no hope of being accepted, so we move to the junk state. From State 0, if we get a 1, then we move to State 01, but if we get a 0, we go to the junk state since the string would then start with 00, which means the string cannot be accepted. Once we get to State 01, whatever symbols come after the initial 01 are of no consequence, as the string starts with 01 and those symbols cannot change that fact. So we stay in that accepting state.
- All strings of the form 0n1 with n ≥ 0. This is all strings that start with any number of 0s (including none) followed by a single 1.

Here State 0n is where we accumulate 0s at the start of the string. When we get a 1, we move to State 0n1. That state is accepting, but if we get anything at all after that first 1, then our string is not of the form 0n1, so we move to the junk state.
- All strings of the form 0101n with n ≥ 0.

To create this DFA, we consider moving along building up the string from λ to 0 to 01 to 010 to 0101. If we get a symbol that doesn't help in this building process, then we go to the junk state. When we finally get to 0101, we are in an accepting state and stay there as long as we keep getting 1s, with any 0 sending us to the junk state.
- All strings in which every 1 is immediately followed by at least two 0s.
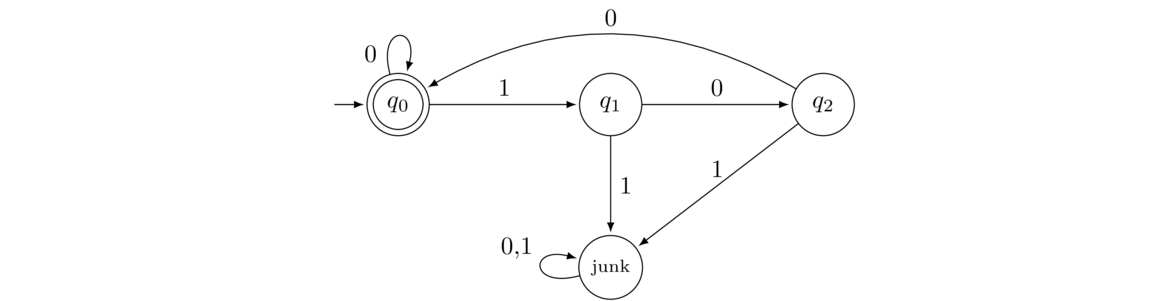
The initial state q0 is an accepting state because initially we haven't seen any 1s, so every 1 is vacuously followed by at least two 0s. And we can stay there if we get 0s since 0s don't cause problems; only 1s do. When we get a 1, we move to q1 where the string has been put on notice, so to speak. If it wants to be accepted, we now need to see two 0s in a row. If we don't get a 0 at this point, we move to the junk state. If we do get a 0, we move to q2, where we still need to see one more 0. If we don't get it, we go to the junk state. If we do get it, then we move back to the accepting state q0. We could move to a separate accepting state if we want, but it's more efficient to move back to q0.
- All strings that end with the same symbol they start with.
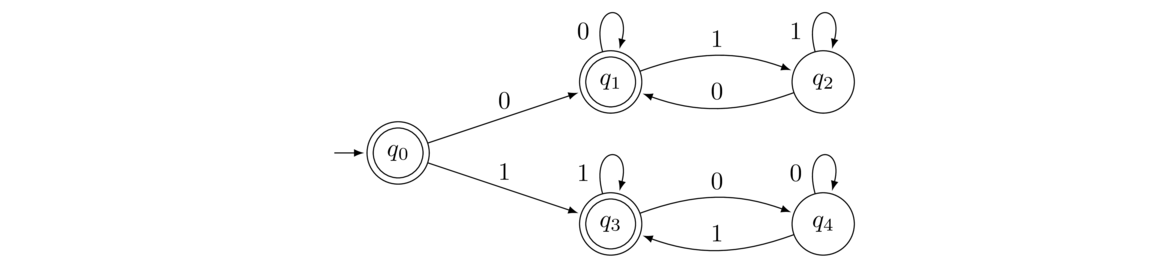
First, the initial state q0 is accepting because the empty string vacuously starts with the same symbol it ends with. From q0 we branch off with a 0 or a 1, sort of like an if statement in a programming language. The top branch is for strings that start with 0, and the bottom is for strings that start with 1. In the top branch, any time we get a 0, we end up in q1, which is accepting, and any time we get a 1, we move to the non-accepting state q2. The other branch works similarly, but with the roles of 0s and 1s reversed.
- All strings whose length is a multiple of 3.

For this DFA, the states 0, 1, and 2 stand for the congruence modulo 3. State 0 is for all strings with a multiple of 3 symbols. State 1 is for all strings that leave remainder 1 when divided by 3, and State 2 is for remainder 2. Any symbol at all moves us from State k to State (k+1) mod 3.
- All strings with an even number of 0s and an even number of 1s.

The state names tell us whether we have an even or odd number of 0s and 1s. For instance EO is an even number of 0s and an odd number of 1s. Once we have these states, the transitions fall into place naturally. For instance, a 1 from State EE should take us to State EO since a 1 will not change the number of 0s, but it will change the number of 1s from even to odd.
- All strings of 0s and 1s.

Since every string is accepted, we only need one accepting state that we start at and never leave.
- All nonempty strings of 0s and 1s.

This is similar to the above, but we need to do a little extra work to avoid accepting the empty string.
- Only the string 001.

Like the 0101n example earlier, we build up symbol-by-symbol to the string 001, with anything not leading to that heading off to a junk state. Once we get to 001, we accept it, but if we see any other symbols, then we head to the junk state.
- Any string except 001.

This is the exact DFA as above but with the accepting and non-accepting states flip-flopped.
- Only the strings 01, 010, and 111.
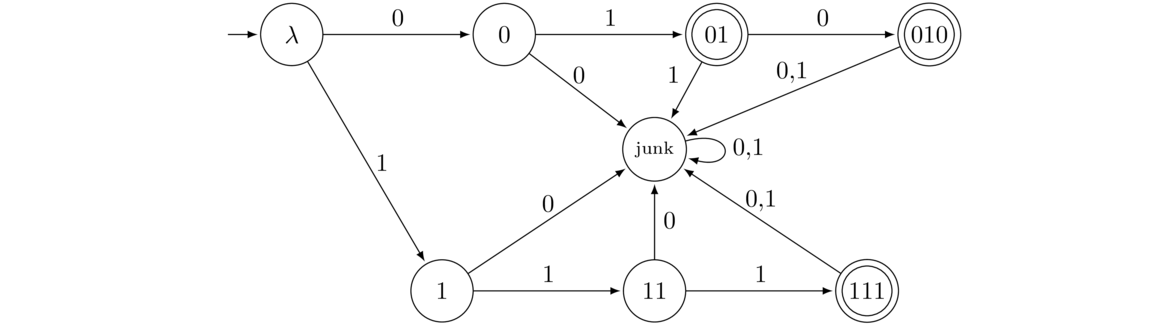
To create this DFA, consider building up the three strings 01, 010, and 111, with anything not helping with that process going to a junk state. A similar approach can be used to build a DFA that accepts any finite language.
- All strings that end in 00 or 01.
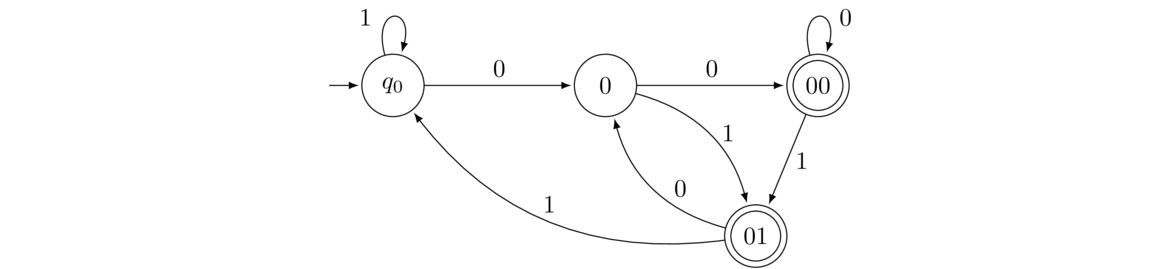
Starting from q0, a 1 doesn't take us any closer to ending with 00 or 01, so we stay put. A 0 takes us to State 0. After that 0, we take note of whether we get a 0 or a 1. Both take us to accepting states. From the 00 accepting state, if we get another 0 we still end with 00, so we stay. Getting a 1 at State 00 means the last two symbols are now 01, so we move to the 01 accepting state. From the 01 accepting state, getting a 1 takes us back to the start, but getting a 0 takes us back to 0 because that 0 takes us part of the way to ending with 00 or 01.
- All strings with at least three 0s and at least two 1s.
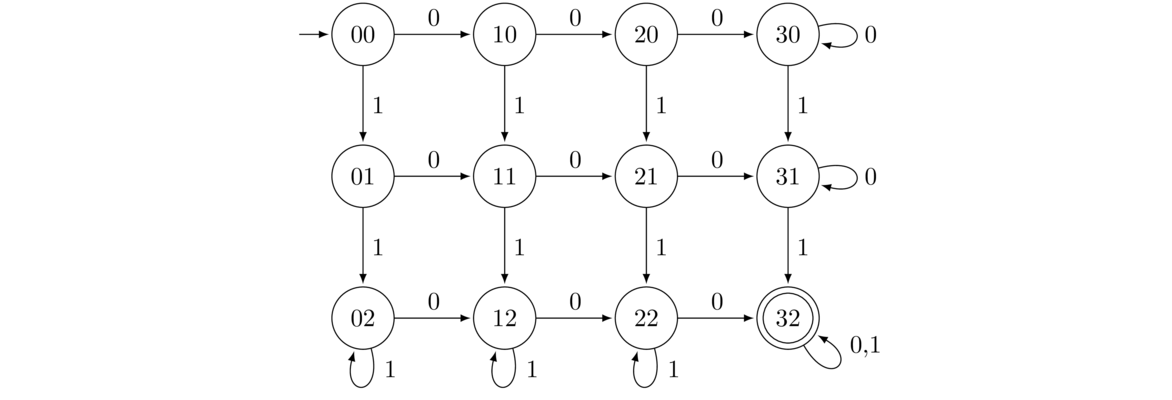
For this DFA, we lay things out in a grid. The labels correspond to how many 0s and 1s we have seen so far. For instance, 21 corresponds to two 0s and one 1. Once we have these states, the transitions fall into place, noting that once we get to the right edge of the grid, we have gotten to three 0s, and getting more 0s doesn't change that we have at least three of them, so we loop. A similar thing happens at the bottom of the grid.
- All strings containing the substring 11001.
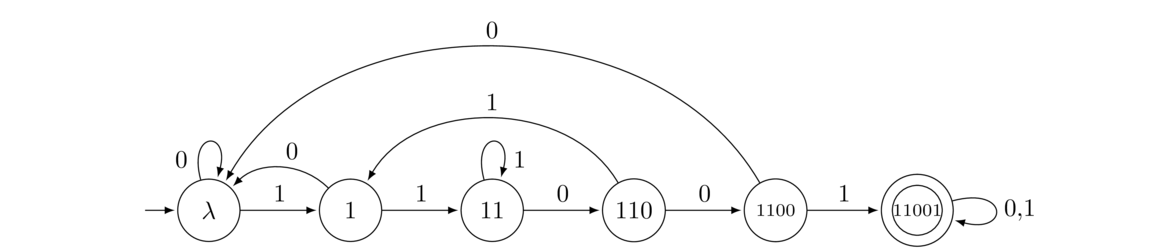
To construct this DFA, we consider building up the substring symbol by symbol. If we get a symbol that advances that construction, we move right, and if we don't, then we move backwards or stay in place. When we get a “wrong” symbol, we don't necessarily have to move all the way back to the start since that wrong symbol might still leave us partway toward completing the substring. For instance, from State 110, if we get a 1, that 1 can be used as the first symbol of a new start at the substring. On the other hand, from State 1100, if we get a 0, then that 0 gives us no start on a new substring, so we have to go back to the start.
Note: There is a nice, free program called JFLAP that allows you to build DFAs by clicking and dragging. It also allows you to run test cases to see what strings are and aren't accepted by the DFA. Besides this, it does a number of other things with automata and languages. See https://www.jflap.org.
Applications of DFAs
A lot of programs and controllers for devices can be thought of as finite state machines. Instead of transitions of 0s and 1s, as in the examples above, the transitions can be various things. And instead of accepting or rejecting an input, we are more interested in the sequence of states the machine goes through.
For example, a traffic light has three states: red, yellow, and green. Transitions between those states usually come from a timer or a sensor going off. A washing machine is another physical object that can be thought of as a state machine. Its states are things like the spin cycle, rinse cycle, etc. Transitions again come from a timer.
As another example, consider a video game where a player is battling monsters. There might be states for when the player is attacking a monster, being attacked, when there is no battle happening, when their health gets to 0, when the monster's health gets to 0, etc. Transitions between the states come from various events.
Thinking about programs as finite state machines in this way can be a powerful way to program.
Nondeterministic Finite Automata
A close relative of the deterministic finite automaton is the nondeterministic finite automaton (NFA). The defining feature of NFAs, not present in DFAs, is a choice in transitions, like below:

With this NFA, a 0 from q0 could either leave us at q0 or move us to q1. This is the nondeterministic part of the name. With an NFA, we don't necessarily know what path an input string will take.
There is a second type of nondeterminism possible:

This is a λ transition. It is sort of like a “free move” where we can move to a state without using up part of the input string. This is nondeterministic because of the choice. We can either take the free move, or use one of the ordinary transitions.
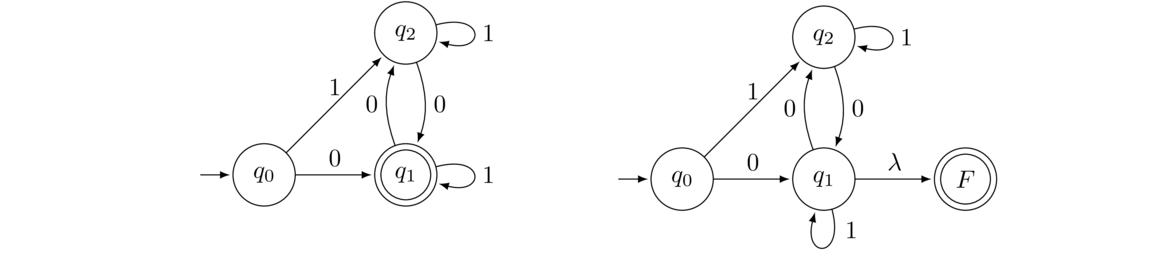
A third feature of NFAs, not present in DFAs, is that we don't need to specify every possible transition from each state. Any transitions that are left out are assumed to go to a junk state. For instance, the NFA on the left corresponds the DFA on the right.

Here is an example NFA:

Consider the input string 11. There are multiple paths this string can lead to. One is q0 → 1 q0 → 1 q1. Another is q0 → 1 q1 → 1 junk (remember that any transitions not indicated are assumed to go to a junk state). The first path leads to an accepting state, while the second doesn't. The general rule is that a string is considered to be accepted if there is at least one path that leads to an accepting state, even if some other paths might not end up at accepting states.
From this definition, we can see that the strings that are accepted by this NFA are all strings that end in 1. We can think about the NFA as permitting us to bounce around at state q0 for as long as we need until we get to the last symbol in the string, at which point we can move to q1 if that last symbol is a 1.
One way to understand how an NFA works is to think in terms of a tree diagram. Every time we have a choice, we create a branch in the tree. For instance, here is a tree showing all the possible paths that the input string 1101 can take through the NFA above.
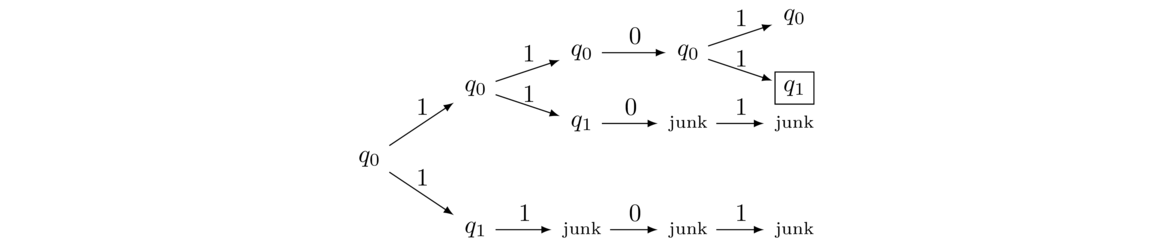
As we see, there are four possible paths. One of them does lead to an accepting state, so the string 1101 is accepted.
We could draw a similar tree diagram for a DFA, but it would be boring. A DFA, being deterministic, leaves no room for choices or branching. Its tree diagram would be a single straight-line path.
Here is another example NFA.

Consider the input string 00. There are again a number of paths that this string can take through the NFA. One possible path through this NFA is q0 → 0 q1 → λ q2 → 0 q2. That is, we can choose to move directly to q1 with the first 0. Then we can take the λ transition (free move) to go to q2 without using that second 0. Then at q2 we can use that 0 to loop. Since we end at the accepting state, the string 00 is accepted. So just to reiterate, think of a λ transition as a free move, where we can move to another state without using up a symbol from the input string.
Nondeterminism
Nondeterminism is a different way of thinking about computing than we are used to. Sometimes people describe an NFA as trying all possible paths in parallel, looking for one that ends in an accepting state.
One way to see the difference between DFAs and NFAs is to think about how a program that simulates DFAs would be different from one that simulates NFAs. To simulate a DFA, our program would have a variable for the current state and a table of transitions. That variable would start at the initial state, and as we read symbols from the input string, we would consult the table and change the state accordingly.
To simulate a nondeterministic machine, we would do something similar, except that every time we come to a choice, where there are two or more transitions to choose from, we would spawn off a new thread. If any of the threads ends in an accepting state, then the input string is accepted. This parallelism allows NFAs to be in some sense faster than DFAs.
Constructing NFAs
Here we will construct some NFAs to accept a given language. Building NFAs requires a bit of a different thought process from building DFAs. Here are the examples we will be doing. It is worth trying them before looking at the answers.
- All strings containing the substring 11001.
- All strings whose third-to-last symbol is 1.
- All strings that either end in 1 or have an odd number of symbols.
- All strings containing the substring 11001.

We earlier constructed a DFA for this language. The NFA solution is a fair bit simpler. The states are the same, but we don't worry about all the backwards transitions. Instead we think of the initial state as chewing up all the symbols of the input string that it needs to until we (magically) get to the point where the 11001 substring starts. Then we march through all the states, arriving at the accepting state, where we stay for the rest of the string.
- All strings whose third-to-last symbol is 1.

We think of the initial state as chewing up all the symbols of the input string we need until we get to the third-to-last symbol. If it is a 1, we can use the 1 transition to q1 and then use the final two symbols to get to the accepting state q3.
- All strings that either end in 1 or have an odd number of symbols.
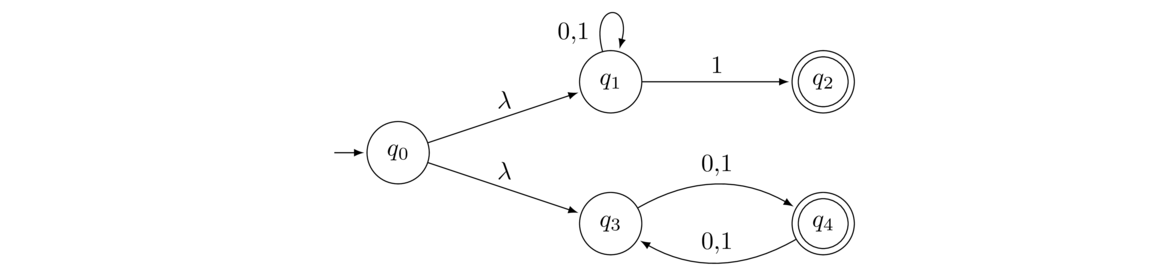
The trick to this problem is to create NFAs or DFAs for strings that end in 1 and for strings with an odd number of symbols. Then we connect the two via the λ transitions from the start state. This gives the NFA the option of choosing either of the two parts, which gives us the “or” part of the problem.
Formal definition of an NFA
The definition of an NFA is the same as that of a DFA except that the transition function δ is defined differently.
For DFAs, the transition function is defined as δ: Q × Σ → Q. Each possible input (state, symbol) pair is assigned an output state. With an NFA, δ is defined as
δ: Q × Σ ∪ {λ} → P(Q). The difference is that we add λ as a possible transition, and the output, instead of being a state in Q, is an element of P(Q), the power set of Q. In other words, the output is a set of states, allowing multiple possibilities (or none) for a given symbol.
One thing to note in particular, is that every DFA is an NFA.
Equivalence of NFAs and DFAs
Question: are there any languages we cannot construct a DFA to accept? Answer: yes, there are many. For instance, it is not possible to construct a DFA that accepts the language 0n1n, which consists of all strings of a number of 0s followed by the same number of 1s. A DFA is not able to remember exactly how many 0s it has seen in order to compare with the number of 1s. Some other things that turn out to be impossible are the language of all palindromes (strings that are the same forward and backward, like 110101011 or 10011001), and all strings whose number of 0s is a perfect square. We will see a little later why these languages cannot be done with DFAs.
The next question we might ask is how much more powerful NFAs are than DFAs. In particular, what languages can we build an NFA to accept that we can't build a DFA to accept? The somewhat surprising answer is nothing. NFAs make it easier to build an automaton to accept a given language, but they don't allow us to do anything that we couldn't already do with a DFA. It's analogous to building a house with power tools versus hand tools—power tools make it easier to build a house, but you can still build a house with hand tools.
To show that NFAs are no more powerful than DFAs, we will show that given an NFA it is possible to construct a DFA that accepts the same language as the NFA. The trick to doing this is something called the powerset construction. It's probably easiest to follow by starting with an example.
Shown below on the left is an NFA and on the right is a DFA that accepts the same language.

Each state of the DFA is labeled with a subset of the states of the NFA. The DFA's initial state, labeled with the subset {1,2}, represents all the states the NFA can be in before any symbols have been read. The 1 comes from the fact that the initial state is 1 and the 2 comes from the fact that we can move to State 2 via a λ move without reading a symbol from the input string.
The 0 transition from that initial state goes to a state labeled with {2,3}. The reason for this if we are in States 1 or 2 of the NFA and we get a 0, then States 2 or 3 are all the possible states we can end up in.
This same idea can be used to build up the rest of the DFA. To determine where a transition with symbol x from a given DFA state S will go, we look at all the NFA states that are in the label of S and see in what NFA states we would end up if we take an x transition from them. The x transition from S goes to a DFA state labeled with a set of all those NFA states. If any of those states is an accepting state, then the DFA state we create will be accepting. The overall idea of this process is that each state of the DFA represents all the possible states the NFA can be in at various points in reading the input string.
Here is a step-by-step breakdown of the process of building the DFA: We start building the DFA by thinking about all the states of the NFA that we can be in at the start. This includes the initial state and anything that can be reached from it via a λ transition. For this NFA those are States 1 and 2. Therefore, the initial state of the DFA we are constructing will be a state with the label 1,2. This is shown below on the left.

Next, we need to know where our initial state will go with 0 and 1 transitions. To do this, we look at all the places we can end up if we start in States 1 or 2 of the NFA and get a 0 or a 1. We can make a table like below to help.
1 → 0 junk 1 → 1 4
2 → 0 2 or 3 2 → 1 3
Putting this together, the 0 transition from the 1,2 state in the DFA will need to go to a new state labeled 2,3 (ignore the junk here). Similarly, the 1 transition from the 1,2 state in the DFA will go to a new state labeled 3,4. Note that since State 4 is accepting in the NFA and the new State 3,4 contains 4, we will make State 3,4 accepting in the DFA. All of this is shown above on the right.
Let's now figure out where the 0 and 1 transitions from the 2,3 state should go. We make the following table looking at where we can go from States 2 or 3 of the NFA:
2 → 0 2 or 3 2 → 1 3
3 → 0 junk 3 → 1 4
So we consolidate this into having 2,3 loop back onto itself with a 0 transition and go to a new state labeled 4 with a 1 transition. See below on the left.
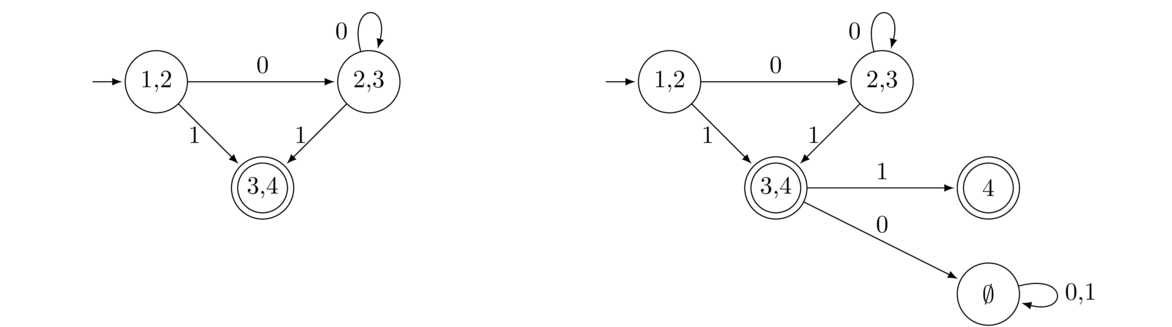
Next, lets look at where the transitions out of State 3,4 must go.
3 → 0 junk 3 → 1 4
4 → 0 junk 4 → 1 junk
Notice that we can go nowhere in the NFA but the implicit junk state with a 0 transition. In other words, there are no real states that we can get to via a 0 from States 3 or 4. This leads us to create a new state labeled ∅ that will act as a junk state in the DFA. Next, as far as the 1 transition goes, the only possibility coming out of States 3 and 4 is to go to 4. See above on the right.
The last step of the process is to figure out the transitions out of the new State 4. There are no transitions out of it in the NFA, so both 0 and 1 will go to the junk State ∅ in the DFA. See above at the start of the problem for the finished DFA.
Here is a second example where the λ transition plays a bit more of a role.
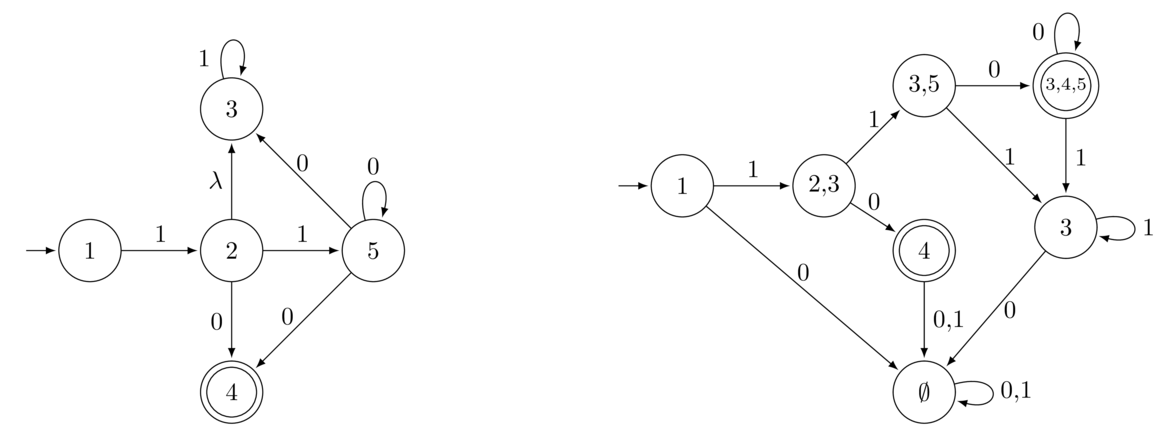
To start, the only state we can be in initially is State 1, so that is our starting state in the DFA. From there, we look at the possibilities from State 1. If we get a 0, we end up in the implicit junk state. If we get a 1, we can end up in States 2 or 3. The reason State 3 is a possibility is that once we get to State 2, we can take the free move (λ) up to State 3. In general, when accounting for λ transitions, we need to be consistent about when we use them, and the rule we will follow is that we only take them at the end of a move (not the beginning). We will leave out the rest of the details about constructing the DFA for this problem in order to not get too bogged down in details. It's a good exercise to try to fill work out the rest of the DFA and make sure you get the same thing as above.
General rules for converting an NFA to a DFA
Here is a brief rundown of the process.
- The initial state of the DFA will be labeled with the initial state of the NFA along with anything reachable from it via a λ transition.
- To figure out the transition from a state S of the DFA with the symbol x, look at all the states in the label of S. For each of those states, look at the x transitions from that state in the NFA. Collect all of the states we can get to from S via an x transition, along with any states we can get to from those states via a λ transition. Create a new state in the DFA whose label is all of the states just collected (unless that state was already created), and add an x transition from S to that state.
- If in the step above, the only state collected is a junk state, then create a new state with the label ∅ (unless it has already been created) and add an x transition from S to that state. This new state acts as a junk state and all possible transitions from that state should loop back onto itself.
- A state in the DFA will be set as accepting if any of the states in its label is an accepting state in the NFA.
General Questions about DFAs and NFAs
In this section we will ask some general questions about DFAs and NFAs.
Complements
If we can build a DFA to accept a language L, can we build one that accepts L? That is, can we build a DFA that accepts the exact opposite of what a given DFA accepts?
The answer is yes, and the way to do it is pretty simple: flip-flop what is accepting and what isn't. For instance, shown below on the left is a DFA accepting all strings whose number of symbols is a multiple of 3. On the right is its complement, a DFA accepting all strings whose number of symbols is not a multiple of 3.

Note that this doesn't work to complement an NFA. This is because acceptance for an NFA is more complicated than for a DFA. If you want to complement an NFA, first convert it to a DFA using the process of the preceding section and then flip-flop the accepting states.
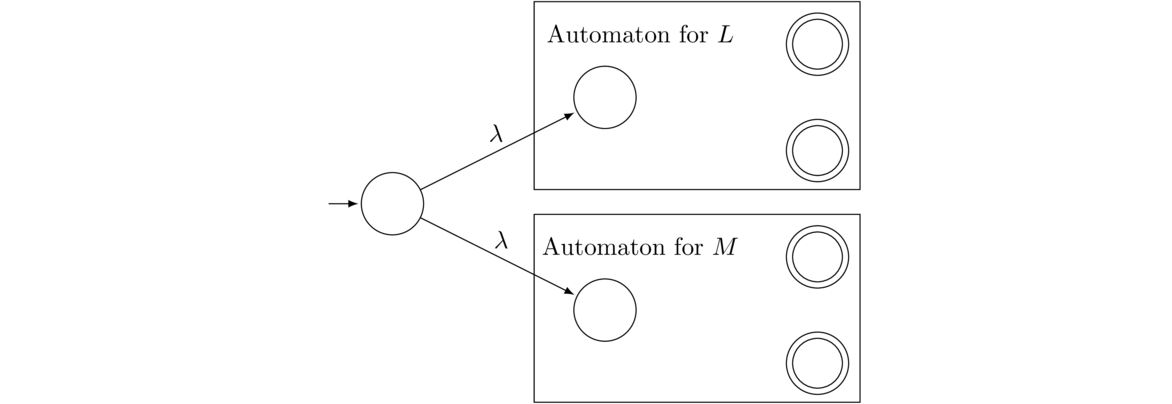
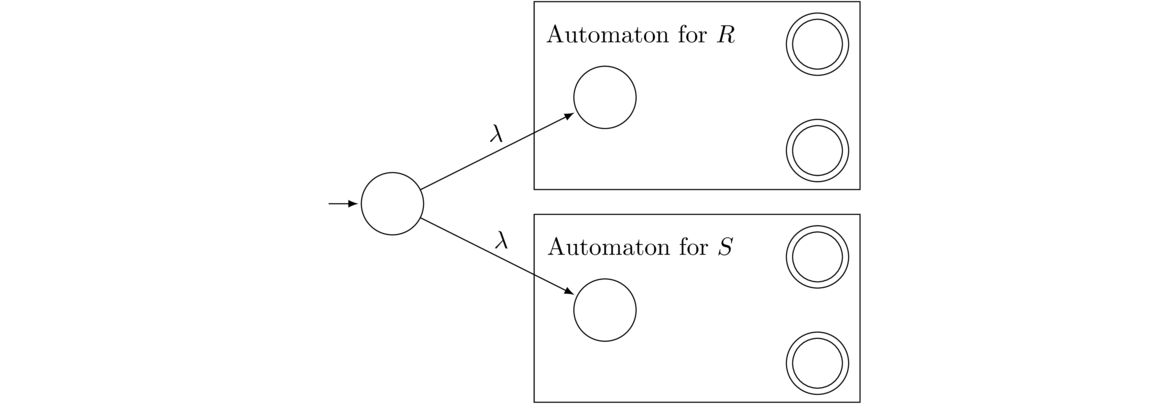
Unions
If we can build NFAs to accept languages L and M, can we build one to accept L ∪ M? Yes. For instance, suppose D is a DFA for all strings with at least two 0s and E is a DFA for all strings with an even number of symbols. Here are both machines:

Here is a machine accepting the union:
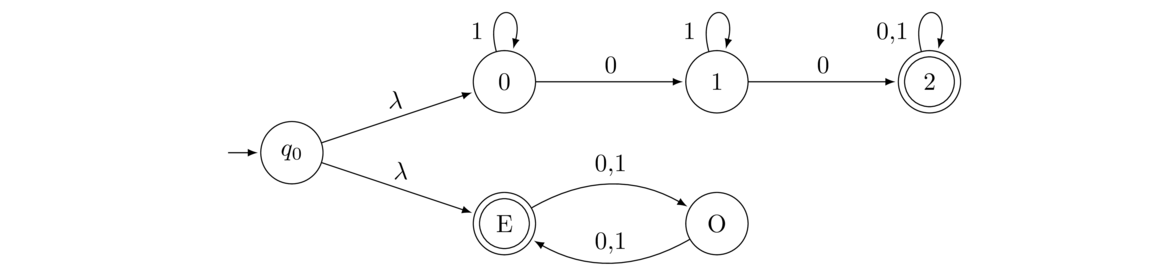
This simple approach works in general to give us an NFA that accepts the union of any two NFAs (or DFAs). Suppose we have two NFAs, as pictured below, that accept languages L and M.

We can create an NFA that accepts L ∪ M by creating a new initial state and creating a λ transition to the initial states of the two NFAs. Those two states cease being initial in the new NFA. Everything else stays the same. See below:
Concatenation
Given NFAs that accept languages L and M, it is possible to construct an NFA that accepts the concatenation LM. The idea is to feed the result of the L NFA into the M NFA. We do this by taking the machine for L and adding λ transitions from its accepting states into the initial state of M. The accepting states of L will lose their accepting status in the machine for LM, and the initial state for M is no longer initial. Everything else stays the same. The construction is illustrated below:

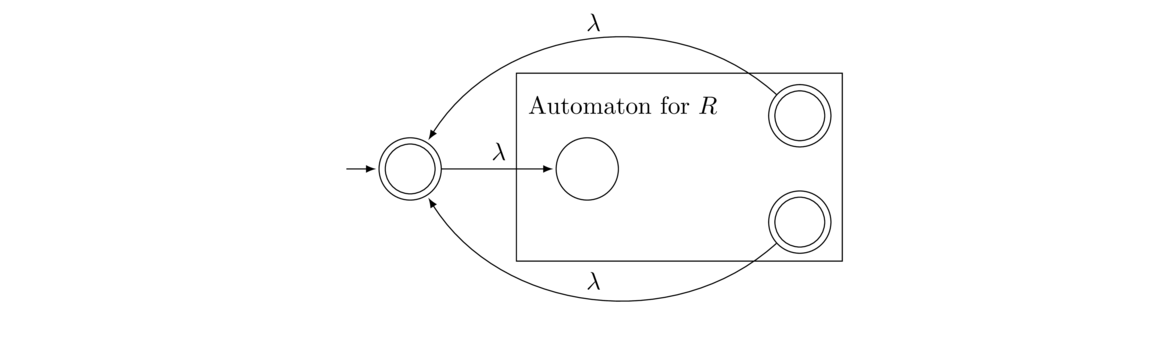
Kleene star
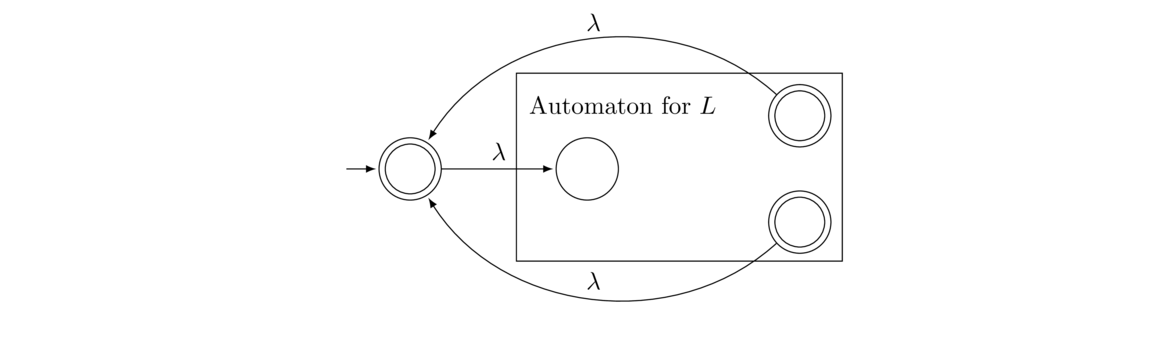
Given an NFA that accepts a language L, is it possible to create an NFA that accepts L*? Recall that L* is, roughly speaking, all the strings we can build from the strings of L.
The answer is yes, and the trick is to feed the accepting states of L back to the initial state with λ transitions. However, we also have to make sure that we accept the empty string, which is a part of L*. It would be tempting to make the initial state of L accepting, which would accomplish our goal. But that could also have unintended consequences if some states have transitions into the initial state. In that case, some strings could end up getting accepted that shouldn't be. It's a good exercise to find an example for why this won't work. So to avoid this problem, we create a new initial state that is also accepting and feeds into the old initial state. The whole construction is shown below.
Intersections
We saw above that there is a relatively straightforward construction that accepts L ∪ M given machines that accept L and M. What about the intersection L ∩ M? There is no corresponding simple NFA construction, but there is a nice way to do this for DFAs.
The trick to doing this can be seen in an earlier example we had about building a DFA to accept all strings with at least three 0s and at least two 1s (Example 18 of Section 2.2). For that example, we ended up building a grid of states, where each state keeps track of both how many zeroes and how many ones had been seen so far.
Given two DFAs D and E, we create a new DFA whose states are D × E, the Cartesian product. So every possible pair of states, the first from D and second from E, will be the states of the intersection DFA. A state in the intersection DFA will be accepting if and only if both parts of the pair are accepting in their respective DFAs.
Transitions are determined by looking at each part separately. For example, to determine the transition for 0 from the state (d1,e1), suppose that in D, that a 0 takes us from d1 to d2 and suppose that in E that a 0 takes us from e1 to e4. Then the 0 transition from (d1,e1) in the intersection will go to (d2, e4).
Here is an example to make all of this clear. Suppose D is a DFA for all strings with at least two 0s and E is a DFA for all strings that end in 1. Here are both machines:

Here is the DFA for the intersection:

One DFA has states 0, 1, and 2, and the other has states N and Y. Thus there are 3 × 2 = 6 states, gotten by pairing up the states from the two DFAs. The only accepting state is (2,Y) since it is the only one in which both pieces (2 and Y in this case) are accepting in their respective DFAs. As an example of how the transitions work, let's look at state (0,N). In the three-state machine, a 0 from State 0 transitions us to State 1, and in the two-state machine, a 0 transition from State N loops from State N to itself. Thus, in the intersection, the 0 transition from (0,N) will go to (1,N).
We could easily turn this into a DFA for the union L ∪ M by changing what states are accepting. The intersection's accepting states are all pairs where both states in the pair are accepting in their respective DFAs. For the union, on the other hand, we just need one or the other of the states to be accepting.
Note that this approach to intersections will not work in general for NFAs. We would have to first convert the NFA into a DFA and then apply this construction.
Other things
There are many other questions we can ask and answer about NFAs and DFAs. For instance, a nice exercise is the following: given an automaton that accepts L, construct an automaton that accepts the reverses of all the strings of L.
Here are some questions we can ask about an automaton.
- Does it accept any strings at all?
- Does it accept every possible string from Σ*?
- Does it accept an infinite or a finite language?
- Given some other automaton, does it accept the same language as this one?
- Given some other automaton, is its language a subset of this one's language?
All of these are answerable. To give a taste of how some of these work, note that we can tell if an automaton accepts an infinite set if there is a cycle (in the graph-theoretic sense) that contains a final state. And we can tell if two automata accept the same language by constructing the intersection of one with the complement of the other and seeing if that automaton accepts anything at all.
In fact, most interesting things we might ask about NFAs and DFAs can be answered little work. As we build more sophisticated types of machines, we will find that this no longer holds—most of the interesting questions are unanswerable in general.
Regular Languages
Regular Expressions
We start with a definition. A regular language is a language that we can construct some NFA (or DFA) to accept. Regular languages are nicely described by a particular type of notation known as a regular expression (regex for short). You may have used regular expressions before in a programming language. Those regular expressions were inspired by the type of regular expressions that we will consider here. These regular expressions are considerably simpler than the ones used in modern programming languages.
Here is an example regex: 0*1(0+1). This stands for any number of 0s, followed by a 1, followed by a 0 or 1. Here is an NFA for the language described by this regex:

Regular expressions are closely related to NFAs. A regular expression is basically a convenient notation for describing regular languages.
Here is a description of what a regular expression over an alphabet Σ can consist of:
- Any symbol from Σ.
- The empty string, λ.
- The empty set, ∅ (this is not used very often).
- The + operator, which is used for the union of two regexes.
- Concatenation, obtained by placing one regex immediately after another.
- The * operator, which is used like the * operator on languages.
- Parentheses, which are used for clarity and order of operations.
Example regular expressions
Here are some small examples. Assume Σ = {0,1} for all of these.
- 01+110 — This describes the language consisting only of the strings 01 or 110, and nothing else.
- (0+1)1 — This is a 0 or a 1 followed by a 1. In particular, it is the strings 01 and 11.
- (0+1)(0+1) — This is a 0 or a 1 followed by another 0 or 1. In particular, it is the strings 00, 01, 10, and 11.
- (0+λ)1 — This is a 0 or the empty string followed by a 1, namely the strings 01 and 1.
- 0* — This is all strings of 0s, including no 0s at all. It is λ, 0, 00, 000, 0000, etc.
- (01)* — This is zero or more copies of 01. In particular, it is λ, 01, 0101, 010101, etc.
- (0+1)* — This is all possible strings of 0s and 1s.
- (0+1)(0+1)* — This is a 0 or 1 followed by any string of 0s and 1s. In other words, it is all strings of length one or more.
- 0*10* — This is any number of 0s, followed by a single 1, followed by any number of 0s.
- 0*+1* — This is any string of all 0s or any string of all 1s.
- λ + 0(0+1)* + 1(0+1)(0+1)* — This is the empty string, or a 0 followed by any string of symbols, or a 1 followed by at least one symbol. In short, it is all strings except a single 1.
Note: The order of operations is that * is done first, followed by concatenation, followed by +. This is very similar to how the order of operations works with ordinary arithmetic, thinking of * as exponentiation, concatenation as multiplication, and + as addition. Parentheses can be used to force something to be done first.
Constructing regular expressions
Just like with constructing automata, constructing regexes is more art than science. However, there are certain tricks that come up repeatedly that we will see. Here are some examples. It's worth trying to do these on your own before looking at the answers. Assume Σ = {0,1} unless otherwise noted.
- The language consisting of only the strings 111, 0110, and 10101
- All strings starting with 0.
- All strings ending with 1.
- All strings containing the substring 101.
- All strings with exactly one 1.
- All strings with at most one 1.
- All strings with at most two 1s.
- All strings with at least two 1s.
- All strings of length at most 2.
- All strings that begin and end with a repeated symbol.
- Using Σ = {0}, all strings with an even number of 0s.
- Using Σ = {0}, all strings with an odd number of 0s.
- All strings with an even number of 0s.
- All strings with no consecutive 0s.
Below are the solutions. Note that these are not the only possible solutions.
- The language consisting of only the strings 111, 0110, and 10101.
Solution: 111 + 0110 + 10101 — Any finite set like this can be done using the + operator.
- All strings starting with 0.
Solution: 0(0+1)* — Remember that (0+1)* is the way to get any string of 0s and 1s. So to do this problem, we start with a 0 and follow the 0 with (0+1)* to indicate a 0 followed by anything.
- All strings ending with 1.
Solution: (0+1)*1 — This is a lot like the previous problem.
- All strings containing the substring 101.
Solution: (0+1)*101(0+1)* — We can have any string, followed by 101, followed by any string. Note the similarity to how we earlier constructed an NFA for a substring.
- All strings with exactly one 1.
Solution: 0*10* — The string might start with some 0s or not. Using 0* accomplishes this. Then comes the required 1. Then the string can end with some 0s or not.
- All strings with at most one 1.
Solution: 0*(λ + 1)0* — This is like the above, but in place of 1, we use (λ + 1), which allows us to either take a 1 or nothing at all. Note also the flexibility in the star operator: if we choose λ from the (λ+1) part of the regex, we could end up with an expression like 0*0*, but since the star operator allows the possibility of none at all, 0*0* is the same as 0*.
- All strings with at most two 1s.
Solution: 0*(λ + 1)0*(λ + 1)0* — This is a lot like the previous example, but a little more complicated.
- All strings with at least two 1s.
Solution: 0*10*1(0+1)* — We can start with some 0s or not (this is 0*). Then we need a 1. There then could be some 0s or not, and after that we get our second required 1. After that, we can have anything at all.
- All strings of length at most 2.
Solution: λ + (0+1) + (0+1)(0+1) — We have this broken into λ (length 0),(0+1) (length 1), or (0+1)(0+1) (length 2). An alternate solution is (λ+0+1)(λ+0+1).
- All strings that begin and end with a repeated symbol.
Solution: (00+11)(0+1)*(00+11) — The (00+11) at the start allows us to start with a double symbol. Then we can have anything in the middle, and (00+11) at the end allows us to end with a double symbol.
- Using Σ = {0}, all strings with an even number of 0s.
Solution: (00)* — We force the 0s to come in pairs, which makes there be an even number of 0s.
- Using Σ = {0}, all strings with an odd number of 0s.
Solution: 0(00)* — Every odd number is an even number plus 1, so we take our even number solution and add an additional 0.
- All strings with an even number of 0s (with Σ = {0,1}).
Solution: (1*01*01*)* + 1* — What makes this harder than the Σ = {0} case is that 1s can come anywhere in the string, like in the string 0101100 containing four 0s. We can build on the (00)* idea, but we need to get the 1s in there somehow. Using (1*01*01*)* accomplishes this. Basically, every 0 is paired with another 0, and there can be some 1s intervening, along with some before that first 0 of the pair and after the second 0 of the pair. We also need to union with 1* because the first part of the expression doesn't account for strings with no 0s.
- All strings with no consecutive 0s.
Solution: 1*(011*)*(0+λ) — Every 0 needs to have a 1 following it, except for a 0 at the end of the string. Using (011*)* forces each 0 (except a 0 as the last symbol) to be followed by at least one 1. We then add 1* at the start to allow the string to possibly start with 1s. For a 0 as the last symbol, we have (0+λ) to allow the possibility of ending with a 0 or not.
Converting Regular Expressions to NFAs
There is a close relationship between regexes and NFAs. Recall that regexes can consist of the following: symbols from the alphabet, λ, ∅, R+S, RS, or R*, where R and S are themselves regexes. Below are the NFAs corresponding to all six of these. Assume that Σ = {0,1}. Notice the similarity in the last three to the NFA constructions for the union, concatenation, and star operation from Section 2.5.
- An NFA for the regex 0.
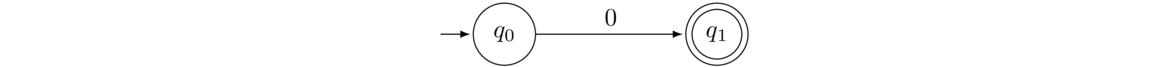
- An NFA for the regex λ.

- An NFA for the regex ∅.

- An NFA for the regex R+S.
- An NFA for the regex RS.

- An NFA for the regex R*.
We can mechanically use these rules to convert any regex into an NFA. For example, here is an NFA for the regex (01+0)*.
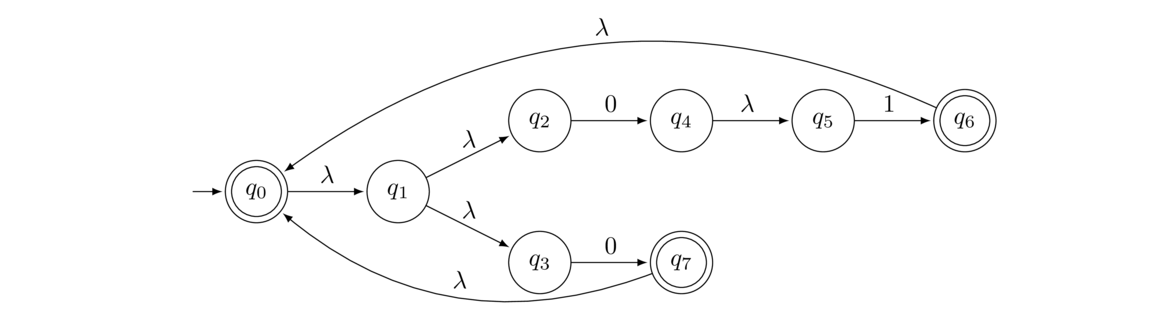
Mechanically applying the rules can lead to somewhat bloated NFAs, like the one above. By hand, it's often possible to reason out something simpler. However, a benefit of the mechanical process is that it lends itself to being programmed. In fact, JFLAP has this algorithm (as well as many others) programmed in. It's worth taking a look at the software just because it's pretty nice, and it's helpful for checking your work.
Converting DFAs to Regular Expressions
We have just seen how to convert a regex to an NFA. Earlier we saw how to convert an NFA to a DFA. Now we will close the loop by showing how to convert a DFA to a regex. This shows that all three objects — DFAs, NFAs, and regexes — are equivalent. That is, they are three different ways of representing the same thing.
To convert DFAs to regexes, we use something called a generalized NFA (GNFA). This is an NFA whose transitions are labeled with regexes instead of single symbols. For instance, the GNFA below means that we move from State 1 to State 2 whenever we read any sequence of 0s followed by a 1.

There is a pretty logical process for converting a DFA into a GNFA that accepts the same language. There are two key pieces, shown below:
- Transitions between the same two states of a GNFA can be combined using the or (+) regex operation, like below (assume that R and S are both regexes):

This applies to loops as well.
- The GNFA shown on the left can be reduced to the one on the right by bypassing the state in the middle.

The idea is that as we move in the left GNFA from q0 to q2, we get R, then we can loop for as long as we like picking up S's on q1, and then we get a T as we move to q2. This is the same as the regex RS*T.
We can combine these operations in a process to turn any DFA into a regex. Here is the process:
- If the initial state of the DFA has any transitions coming into it, then create a new initial state with a λ transition to the old initial state.
- If any accepting state has a transition going out of it to another state, or if there are multiple accepting states, then create a new accepting state with λ transitions coming from the (now no longer) accepting states into the new accepting state.
- Repeatedly bypass states and combine transitions, as described earlier, until only the initial state and final state remain. The regex on the transition between those two states is a regex that accepts the same language as the original DFA. States can be bypassed in any order.
Examples
Convert the DFA below on the left into a regex.
To start, the initial state has no transitions into it, so we don't need to add a new initial state. However, the final state does have a transition out of it, so we add a new final state, as shown above on the right.
Now we start bypassing vertices. We can do this in any order. Let's start by bypassing q2. To bypass it, we look for all paths of the form x → q2 → y, where x and y can be any states besides q2. There are two such paths: q0 → q2 → q1 and q1 → q2 → q1. The first path generates the regex 11*0 and the second generates the regex 01*0. These paths are shown below.

The resulting GNFA is shown below on the left. We then combine the two paths from q0 to q1 and the two loops on q1, as shown on the right.

Next, let's bypass q1. The result is shown below.
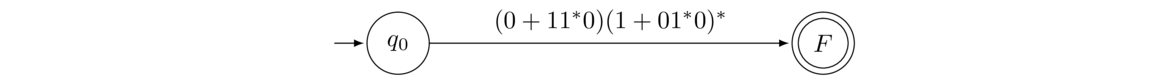
Only the initial and accepting states are left, so we have our answer: (0+11*0)(1+01*0)*
Convert the DFA below on the left into a regex.

The start state has a transition (a loop) coming into it, and there are multiple accepting states, so add a new start state and a new accepting state, like below.

Now we can start bypassing states. Right away, we can bypass q3 easily. There are no paths of the form x → q3 → y that pass through it (it's a junk state), so we can safely remove it. Let's then bypass q0. The only path through it is I → q0 → q1. The result of bypassing it (and removing q3) is shown below.

Next, let's remove q1. There are paths I → q1 → q2 and I → q1 → F that pass through q1. The result of bypassing q1 is shown below on the left. After that, we bypass q2 and combine the two transitions from I to F to get our final solution, shown at right.

Therefore, the regex matching our initial DFA is 0*10*10*+0*10*.
Non-Regular Languages
Not all languages are regular. One example is the language 0n1n of all strings with some number of 0s followed by the same number of 1s. Another example is the language of all palindromes — strings that read the same forward as backwards (like 0110 or 10101).
If we want to show that a language is not regular, then according to the definition, we would need an argument to explain why it would be impossible to construct an NFA (or equivalently an DFA or regex) that accepts the language. The most common technique for doing this is the Pumping Lemma.
Here is the main idea behind the Pumping Lemma: If you feed an NFA an input string that is longer than the number of states into the automaton, then by the pigeonhole principle, some state will have to be visited more than once. That is, there will be a “loop” in the in the sequence of states that the string takes through the automaton. See the figure below.
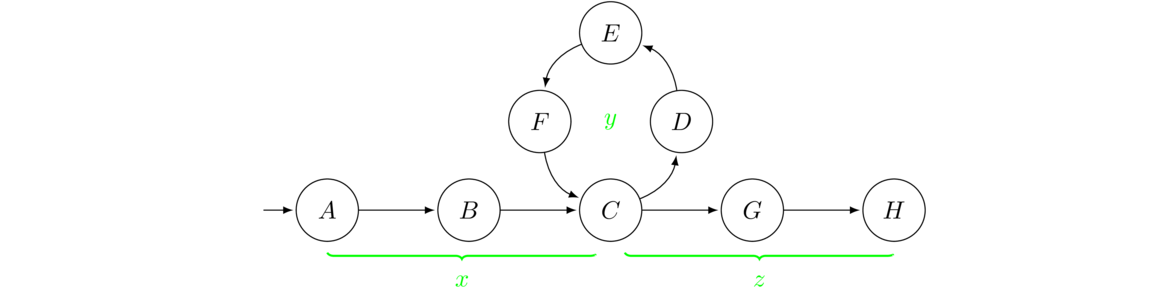
The figure above shows the sequence of states a certain input string might travel through. Imagine that the string as broken up into xyz, where x is the part that takes the machine from A to C, y is the part that takes the machine from C back to C along the loop, and z is the part that takes the machine from C to H. The string xyz is in the language accepted by the machine, as is the string xy2z, which comes from taking the loop twice. This is called “pumping up” the string xyz to obtain a new string in the language.
There is no restriction on how many times we take the loop, so we can pump the string up to xykz for any k > 0, and we can even “pump it down” to xy0z (which is xz) by skipping the loop entirely.
We can use this idea to show the language of all strings of the form 0n1n is not regular. These are all strings that contain a string of 0s followed by a string of the same amount of 1s. Suppose there exists a DFA for it. Let k be the number of states in the DFA, and look at the string 0k+11k+1, which is accepted by the DFA. The first part of the string, the 0k+1 part has more 0s than there are states in the machine, so there must be a cycle, and the cycle must only involve 0s. We can then pump up that cycle to get another string that is accepted. However, when we pump up the cycle, we end up getting more 0s giving us a string that has more 0s than 1s. But this is not a string in the language, so we have a contradiction. The DFA can't possibly exist because it leads to an impossible situation.
We can formalize all of this into a technique for showing some languages are not regular. We use this pumping property, that given any string whose length is longer than the number of states in an NFA for that language, we can find a way to break it into xyz such that xykz is also in the language. This is the called the Pumping Lemma. Here is a rigorous statement of it.
Pumping Lemma. If L is a regular language, then there is an integer n such that any string in L of length at least n can be broken into xyz with |xy| ≤ n and |y| > 0 such that xykz is also in L for all k ≥ 0.
Note the restrictions on the lengths of xy and y given above. The restriction |xy| ≤ n says that the “loop” has to happen within the first n symbols of the string, and the restriction |y| > 0 says there must be a (nonempty) loop.
The Pumping Lemma gives us a property that all regular languages must satisfy. If a language does not satisfy this property, then it is not regular. This is how we usually use the Pumping Lemma — we find a (long enough) string in the language that cannot be “pumped up”.
The first time through, it can be a little tricky to understand exactly how to use the Pumping Lemma, so it is often formulated as a game, like below:
- First, your opponent picks n.
- Then you pick a string s of length at least n that is in the language.
- Your opponent breaks s into xyz however they want, as long as the breakdown satisfies that |xy| ≤ n and |y| > 0.
- Then you show that no matter what breakdown they picked, there is a k ≥ 0 such that xykz is not in the language.
Here a few key points to remember:
- The opponent chooses n, not you.
- Your string must be of length at least n and must be in the language.
- You don't get to pick the breakdown into xyz. Your opponent does. You need a logical argument that shows why all possible breakdowns the opponent chooses will fail.
In terms of playing this game, try to choose s so that the opponent is forced into picking an x and y that are advantageous to you. Also, in the last step, a lot of the time k = 2 or k = 0 is what works. Here are some examples.
Show the language of all strings of the form 0n1n is not regular.
First, let n be given. We choose s = 0n1n. Then suppose s is broken into xyz with |xy| ≤ n and |y| > 0. Because |xy| ≤ n, and s starts with the substring 0n, we must have that x and y both consist of all 0s. Therefore, since |y| > 0, xy2 will consist of more 0s than xy does. Hence xy2z will be of the form 0k1n with k > n, which is not in the language. Thus the language fails the pumping property and cannot be regular.
As an example of what we did above, consider n = 4. In that case, we pick s = 00001111. There are a variety of breakdowns our opponent could use, as shown below.

The key is that since |xy| < 4, we are guaranteed that x and y will lie completely within the first block of 0s. And since |y| > 0, we are guaranteed that y has at least one 0. Thus when we look at xy2, we know it will contain more 0s than xy. So xy2z will have more 0s than 1s and won't be of the right form.
If the opponent, for instance, chooses the breakdown above on the left, then xy2 will become 000000 and xy2z becomes 0000001111, which is no longer of the proper form for strings in the language.
Show that the language of all palindromes on Σ = {0,1} is not regular.
First, let n be given. We choose s = 0n10n. This is a palindrome of length at least n. Now suppose s is broken into xyz with |xy| ≤ n and |y| > 0. Since |xy| ≤ n, we must have x and y contained in the initial substring 0n of s. Hence x and y consist of all 0s. Therefore, since |y| > 0, the string xy2z will be of the form 0k10n with k > n. This is not a palindrome, so it is not in the language. Therefore, the pumping property fails and the language is not regular.
Show that the language on Σ = {0} of all strings of the form 0p, where p is prime, is not regular.
First, let n be given. We choose s = 0p, where p is the first odd prime greater than n. Now suppose s is broken into xyz with |xy| ≤ n and |y| > 0. Consider the string xyp+1z, where we pump up the string p+1 times. We can think of it as consisting of x followed by p copies of y, followed by y again, followed by z. So it contains all of the symbols of s along with p additional copies of y. Thus we have
The number (p+1)|y| cannot be prime. If |y| > 1, then (p+1)|y| is the product of two numbers greater than 1, making it not prime, and if |y| = 1, then (p+1)|y| = p+1, which can't be prime because p is an odd prime, making p+1 is even. Thus the pumping property fails, and the language is not regular.
An interesting thing happens if we try to show that the language of all strings of the form 0c, where c is composite (a non-prime), is not regular. Any attempts to use the Pumping Lemma will fail. Yet the language is still not regular. So the Pumping Lemma is not the be-all and end-all of showing things are not regular. However, we can indirectly use the Pumping Lemma. Recall that if we can construct a DFA that accepts a language, then we can easily construct one that accepts the language's complement by flipping the accepting and non-accepting states. So if we could build a DFA for composites, then we could build one for primes by this flip-flop process. But we just showed that primes are not regular, which means there is no DFA that accepts primes. Thus, it would be impossible to build one for composites.
Just to examine the Pumping Lemma a little further, suppose we were to try to use it to show that the language given by the regex 0*1* is not regular. This language is obviously regular (since it is given by a regular expression), so let's see where things would break down. Suppose n is given and we choose s = 0n1n. Suppose the opponent chooses the breakdown where x is empty, y is the first symbol of the string, and z is everything else. No matter how we pump the string up into xykz, we always get a string that fits the regex 0*1*. We aren't able to get something not in the language. So our Pumping Lemma attempt does not work.
What is and isn't regular
Anything that we can describe by a regular expression is a regular language. This includes any finite language, and many other things. Regular languages do not include anything that requires sophisticated counting or keeping track of too much. For instance, 0n1n requires that we somehow keep count of the number of 0s we have seen, which isn't possible for a finite automaton. Similarly, palindromes require us to remember any arbitrarily large number of previous symbols to compare them with later symbols, which is also impossible for a finite automaton.
We have also seen that we can't tell if a string has a prime length. Generally, finite automata are not powerful enough to handle things like primes, powers of two, or even perfect squares. They can handle linear things, like telling if a length is odd or a multiple of 3, but nothing beyond that.
Context-Free Grammars
Definitions and Notations
A grammar is a way of describing a language. Grammars have four components:
- A finite set of items called terminals.
- A finite set of items called variables or non-terminals.
- A specific variable S that is the start variable.
- A finite set of rules called productions that specify substitutions, where a string of variables and terminals is replaced by another string of variables and terminals.
The grammars we will be considering here are context-free grammars, where all the productions involve replacing a single variable by a string of variables and terminals. Here is an example context-free grammar:
A → aB | λ
B → bBb | BB | ab
Let's identify the different parts of this grammar:
- In these notes, our variables will always be capital letters, and our terminals will always be lowercase letters or numbers. So in the grammar above, A and B are the variables, while a and b are the terminals. The empty string λ is also a terminal.
- The production A → aB | λ gives the possible things we can replace A with. Namely, we can replace it with aB or with the empty string. The | symbol in a production is read as “or”. It allows us to specify multiple rules in the same line. We could also separate this into two rules A → ab and A → λ.
- The start variable is A. The start variable is always the one on the left side of the first production.
For any grammar, the language generated by the grammar is all the strings of terminals it is possible to get by beginning with the start variable and repeatedly applying the productions (i.e. making substitutions allowed by the productions.)
Here is an example of using the grammar to generate a string. Starting with A in the grammar above, we can apply the rule A → aB. Then we can apply the rule B → BB to turn aB into aBB. Then we can apply the rule B → ab to the first B to get aabB. After that, we can apply the rule B → bBb to get aabbBb. Finally, we can apply the rule B → ab to get the aabbabb. This is one of the many strings in the language generated by this grammar.
We can display the sequence of substitutions above like below (new substitutions shown in bold):
This is called a derivation. When doing derivations, there can sometimes be a choice between two variables as to which one to expand first, like above where we have aBB. Often it doesn't matter, but sometimes it helps to have a standard way of doing things. A leftmost derivation is one such standard, where we always choose the variable farthest left as the one to expand first.
A second way of displaying a sequence of substitutions is to use a parse tree. Here is a parse tree for the string derived above.
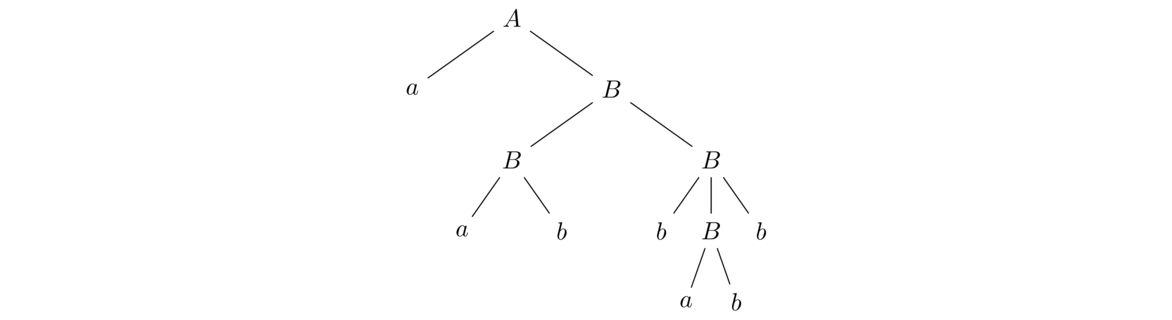
The string this derives can be found by reading the terminals from the ends of the tree (its leaves) from left to right (technically in a preorder traversal).
There may be multiple possible parse trees for a given string. If that's the case, the grammar is called ambiguous.
Examples
Finding the language generated by a grammar
- Find the language generated by this grammar:
A → aA | λ
One approach is to start with the start variable and see what we can get to. Starting with A, we can apply A → aA to get aA. We can apply it again to get aaA. If we apply it a third time, we get aaaA. We can keep doing this for as long as we like, and we can stop by choosing A → λ at any point. So we see that this grammar generates strings of any number of a's, including none at all. It fits the regular expression a*.
Notice the recursion in the grammar's definition. The variable A is defined in terms of itself. The rule A → λ acts as a base case to stop the recursion.
- Find the language generated by this grammar:
S → AB
A → aA | λ
B → bB | b
Notice that the grammar for A is the same as the grammar from the previous problem. The grammar for B is nearly the same. The B → b production, however, does not allow the possibility of no bs at all. We must have at least one b.
The first production, S → AB, means that all strings generated by this grammar will consist of something generated by A followed by something generated by B. Thus, the language generated by this grammar is all strings of the form a*bb*; that is, the language is all strings consisting of any number of a's followed by at least one b.
- Find the language generated by this grammar:
S → A | B
A → aA | λ
B → bB | b
This is almost the same grammar as above, except that S → AB has been replaced with S → A | B. Remember that | means “or”, so the language generated by this grammar is all strings that are either all a's or at least one b. As a regular expression, this is a*+bb*.
- Find the language generated by this grammar:
S → 0S1 | λ
Let's look at a typical derivation:
S ⇒ 0S1 ⇒ 00S11 ⇒ 000S111 ⇒ 000111We see that every iteration of the process generates another 0 and another 1. So the language generated by this grammar is all strings of the form 0n1n for n ≥ 0.
Recall that 0n1n is not a regular language, so this example shows that context-free grammars can do things that NFAs and DFAs can't.
- Find the language generated by this grammar:
S → aSa | bSb | a | b | λ
Let's look at a typical derivation:
S ⇒ aSa ⇒ aaSaa ⇒ aabSbaa → aabbaaWe see that each a comes with a matching a on the other side of the string and likewise with each b. This forces the string to read the same backwards as forwards. This grammar generates all palindromes.
- Find the language generated by this grammar, where the symbols ( and ) are the terminals of the grammar:
S → SS | (S) | λ
This is an important grammar. It generates all strings of balanced parentheses. The production S → (S) allows for nesting of parentheses, and the production S → SS allows expressions like ()(), where one set of parentheses closes and then another starts.
Creating grammars
Now let's try creating grammars to recognize given languages. Here are the problems first. It's a good idea to try them before looking at the answers. Assume Σ = {a,b} unless otherwise noted.
- All strings of a's containing at least three a's.
- All strings of a's and b's.
- All strings with exactly three a's.
- All strings with at most three a's.
- All strings with at least three a's.
- All strings containing the substring ab.
- All strings of the form ambncn for m,n ≥ 0.
- All strings of the form ambn with m > n ≥ 0.
- All strings of the form ambncm+n with m,n ≥ 0.
- All strings of the form akbmcn with n = m or n = k and k,m ≥ 0.
- All strings where the number of a's and b's are equal.
Here are the solutions.
- All strings of a's containing at least three a's.
A → aA | aaa
The grammar we did earlier, A → aA | λ, is a useful thing to keep in mind. Here we modify it so that instead of stopping the recursion at an empty string, we stop at aaa, which forces there to always be at least three a's.
- All strings.
S → aS | bS | λ
The idea behind this is that at each step of the string generation, we can recursively add either an a or a b. So this grammar builds up strings one symbol at a time. For instance, to derive the string abba, we would do S ⇒ aS ⇒ abS ⇒ abbS ⇒ abbaS ⇒ abba.
- All strings with exactly three a's.
S → BaBaBaB
B → bB | λ
We use the B production to get a (possibly empty) string of bs. Then we imagine the string as being constructed of three a's, with each preceded and followed by a (possibly empty) string of b's.
- All strings with at most three a's.
S → BABABAB
A → a | λ
B → bB | λ
This is similar to the above, but instead of using the terminal a in the S production, we use A, which has the option of being a or empty, allowing us to possibly not use an a.
- All strings with at least three a's.
S → TaTaTaT
T → aT | bT | λ
This is somewhat like the previous two examples. In the S production, we force there to be three a's. Then before, after, and in between those a's, we have a T, which allows any string at all.
- All strings containing the substring ab.
S → TabT
T → aT | bT | λ
This is similar to the previous example in that we force the string to contain ab, while the rest of the string can be anything at all.
- All strings of the form ambncn for m,n ≥ 0.
S → AT
A → aA | λ
T → bTc | λ
All strings in this language consist of a string of a's followed by a string containing a bunch of b's followed by the same number of c's. We have a production A that produces a string of A's and a production T that produces bncn. We join them together with the production S → AT.
- All strings of the form ambn with m > n ≥ 0.
S → AT
A → aA | a
T → aTb | λ
This is similar to the previous example. The strings in this language can be thought of as consisting of some nonzero number of a's followed by a string of the form anbn.
- All strings of the form ambncm+n with m,n ≥ 0.
One approach would be to try the following.
S → aSc | bSc | λ
Every time we get an a or a b, we also get a c. This allows the number of a's and b's combined to equal the number of c's. However, there is the possibility for the a's and b's to come out of order, as in the derivation S ⇒ aSc ⇒ abScc ⇒ abaSccc ⇒ abaccc. To fix this problem, do the following:
S → aSc | T | λ
T → bTc | λ
It's still true that every time we get an a or a b, we also get a c. However, now we can't get any b's until we are done getting a's.
- All strings of the form akbmcn with n = m or n = k and k,m ≥ 0.
S → AT | U
A → aA | λ
T → bTc | λ
U → aUc | B
B → bB | λ
The key here is to break it into two parts: n = m or n = k. The S → AT production handles the n = m case by generating strings that start with some number of a's followed by an equal number of b's and c's. Then S → U production handles the n = k case by using U → aUc to balance the a's and c's and using U → B to allow us to insert the b's once we are done with the a's and c's.
- All strings where the number of a's and b's are equal.
S → SS | aSb | bSa | λ
The productions S → aSb and S → bSa guarantee that whenever we get an a, we get a b elsewhere in the string and vice-versa. However, these productions alone will not allow for a string that starts and ends with the same letter like abba. The production S → SS allows for this by allowing two derivations to essentially happen side-by-side, like in the parse tree below for abba.
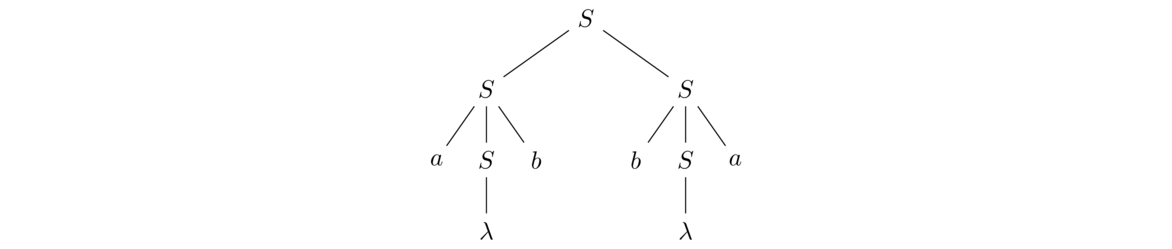
A longer string like abbaabba could be generated by applying the S → SS production multiple times.
A few practical grammar examples
One very practical application of grammars is they can be used to describe many real-world languages, such as programming languages. Most programming languages are defined by a grammar. There are automated tools available that read the grammar and generate C or Java code that reads strings and parses them to determine if they are in the grammar, as well as breaking them into their component parts. This greatly simplifies the process of creating a new programming language. Here are a few more examples.
Here is a grammar for some simple arithmetic expressions.
E → E+E | E*E | a | b | c
This grammar generates expressions like a+b+c or a*b+b*a. It's not hard to expand this into a grammar for all common arithmetic expressions. However, one problem with this grammar is that it is ambiguous. For example, the string a*b+c has two possible parse trees, as shown below.
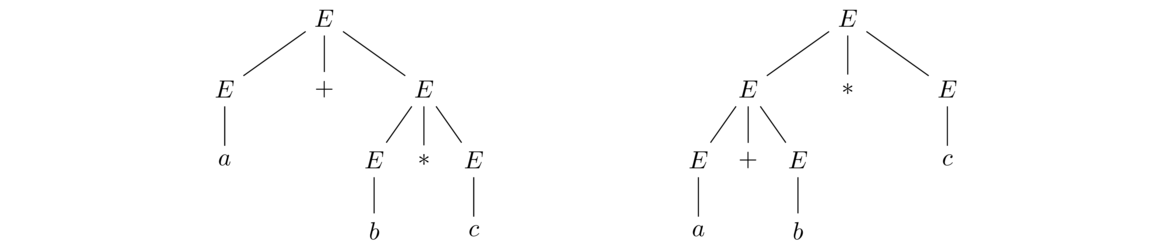
The two parse trees correspond to interpreting the expression as (a+b)*c or a+(b*c). This type of ambiguity is not desirable in a programming language. We would like there to be one and only one way to derive a particular string. It wouldn't be good if we entered 2+3*4 into a programming language and could get either 20 or 14, depending on the compiler's mood. There are ways to patch up this grammar to remove the ambiguity. Here is one approach:
E → E+M | M
M → M*B | B
B → a | b | c
The idea here is we have separated addition and multiplication into different rules. There is a lot more to creating grammars for expressions like this. If you're interested, see any text on programming language theory.
One interesting note about ambiguity is that there are some languages for which any grammar for them will have to be ambiguous, with no way to remove the ambiguity. The standard example of this is the language ambmcn with m,n ≥ 0.
Here is another practical grammar. It generates all valid real numbers in decimal form.
S → -N | N
N → D.D | .D | D
D → ED | E
E → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
In constructing this, the idea is to break things into their component parts. The production for S has two options to allow for negatives or positives. The next production covers the different ways a decimal point can be involved. The last two productions are used to create an arbitrary string of digits.
Below is a grammar for a very simple programming language. For clarity, the grammar's variable names are multiple letters long. To tell where a variable name starts and ends, we use ⟨ and ⟩.
⟨ Expr ⟩ → ⟨ Loop ⟩ | ⟨ Print ⟩
⟨ Loop ⟩ → for ⟨ var ⟩ = ⟨ Int ⟩ to ⟨ Int ⟩ ⟨ Block ⟩
⟨ Var ⟩ → a | b | c | d | e
⟨ Int ⟩ → ⟨ Digit ⟩ ⟨ Int ⟩ | ⟨ Digit ⟩
⟨ Digit ⟩ → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
⟨ Block ⟩ → { ⟨ ExprList ⟩ }
⟨ ExprList ⟩ → ⟨ ExprList ⟩ ⟨ Expr ⟩ | λ
⟨ Print ⟩ → print "⟨ String ⟩ "
⟨ String ⟩ → ⟨ String ⟩ ⟨ Symbol ⟩ | λ
⟨ Symbol ⟩ → a | b | c | d | e | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
This grammar produces a programming language that allows simple for loops and print statements. Here is an example string in this language (with whitespace added for clarity):
for a = 1 to 5 {
for b = 2 to 20 {
print("123")
}
}
Grammars and Regular Languages
Converting NFAs into context-free grammars
Many of the example grammars we saw were for regular languages. It turns out to be possible to create a context-free grammar for any regular language. The procedure is a straightforward conversion of an NFA to a context-free grammar. On the left below is an NFA, and on the right is a grammar that generates the same language as the one accepted by the NFA.

Each state becomes a variable in the grammar. The start state becomes the start variable. A transition like A → 1B becomes the production A → 1B. A λ transition like B → λC becomes the production B → C. Any final state gets a λ production.
Tracing through a derivation in the grammar exactly corresponds to moving through the NFA. For instance, the derivation A ⇒ 0A ⇒ 01B ⇒ 01C ⇒ 01 corresponds to moving from A to A to B to C in the NFA.
Converting certain context-free grammars into NFAs
We have seen that some context free grammars generate languages that are not regular. The standard example is S → 0S1 | λ, which generates the language 0n1n. So we can't convert every context-free grammar to an NFA. But we can convert certain grammars that are known as right-linear grammars.
A right linear grammar is one in which the right side of every production is either a string of terminals or a string of terminals followed by a single variable. Not coincidentally, the grammar just generated above from the NFA is a right-linear grammar. More or less the reverse of the process above for converting NFAs into grammars will work to convert a right-linear grammar into an NFA. There are a couple of small tricks involved, however. Below is an example. On the left is a grammar and on the right is an NFA that accepts the same language as the one generated by the grammar.
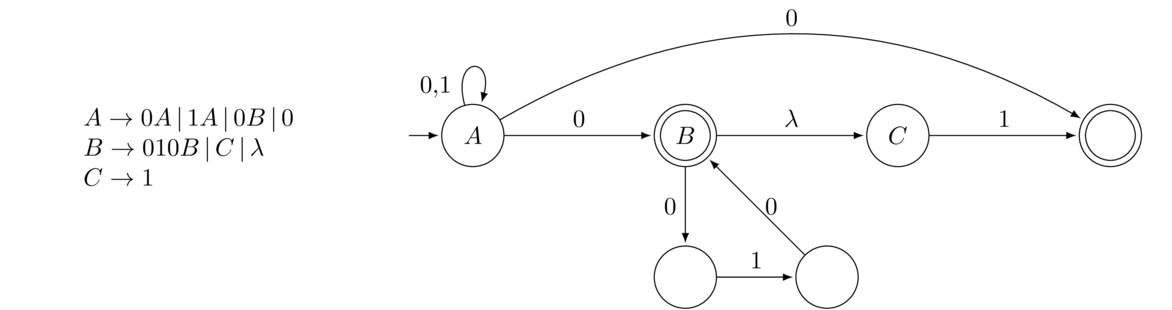
Each variable becomes a state of the NFA, with the start variable becoming the start state. Any variable with a λ production becomes an accepting state. A production like A → 0B becomes a transition of the form A → 0 B. This is all the reverse of the earlier process.
One tricky thing is how to handle A → 0 and C → 1. We do this by creating a new accepting state along with a 0 transition to it from A and a 1 transition from C.
The other tricky thing is how to handle B → 010B. We create new intermediate states to handle each of the terminals, as shown in the figure.
Regular languages and grammars
The result of these two procedures is that, in addition to DFAs, NFAs, and regular expressions, we now have a fourth way of describing regular languages: right-linear grammars. In particular, all four models are equivalent.
Further, this shows that regular languages are a subset of the languages generated by context-free grammars. And it is a strict containment, as the language 0n1n shows. One consequence is that context-free grammars are more powerful than NFAs.
Note that there's nothing special about right-linear grammars vs. left-linear grammars (where the variable comes before the string of terminals). Regular languages can also be described by these. We just have to be careful not to mix left and right in the same grammar, as that type of grammar (called a linear grammar) is actually more powerful than left-linear or right-linear alone.
Chomsky Normal Form
There are several places in the theory of context-free grammars where allowing an arbitrary context-free grammar leads to a lot of annoying special cases to deal with. There is a standard form, called Chomsky normal form (CNF), that helps with this. In CNF, the right side of every production has either a single terminal or exactly two variables. Further, the start variable cannot appear on the right side of any production, and λ cannot appear on the right side either, except possibly as the right side of the start variable. We can go through the sequence of steps below to convert any context-free grammar to CNF.
- Make it so that the start variable is not on the right side of any production.
- Remove all λ productions (productions like A → λ).
- Remove all unit productions (productions like A → B, where the right side is a single variable).
- Make it so that no terminals appear on the right side of any production except by themselves, and break up any long productions of three or more variables. At the end, the right sides of all productions will have either a single terminal or exactly two variables (like A → a or A → BC, for instance).
Each of these steps follows a fairly logical process.
- Start variable on right side — If the start variable S is on the right of some production, then create a new start variable S0 and add the production S0 → S. For instance, suppose we have the grammar below.
S → AS | b
A → aA | a
We would change it into the following:
S0 → S
S → AS | b
A → aA | a
The new start variable S0 is guaranteed to not appear on the right side.
- Removing λ productions — To remove a production like A → λ, we simulate the process of replacing A with λ in a derivation by doing that in the grammar itself. For instance, suppose we have the grammar below.
S → ABAb
A → aB | λ
B → bB | bbA
To remove A → λ, start by looking at the first production. We consider all the ways we could set A to λ there. This means that for each A, we can imagine leaving it alone or deleting it, and we look at all the possible combinations of doing that. The S production then becomes
S → ABAb | BAb | ABb | Bb
The first production corresponds to removing no A's. The next two correspond to the two ways of removing one A, and the last comes from removing both A's.
For the given grammar, A also shows up in one of B's productions, so we also need to go through the process on B. Here is the finished product after everything has been done:
S → ABAb | BAb | ABb | Bb
A → aB
B → bB | bbA | bb
Sometimes this process can go multiple levels deep. For instance, if the above grammar had a production like B → AA, then that production would become B → AA | A | λ, and then we would have a new λ production to remove.
- Removing unit productions — A production like A → B that involves a single variable being replaced by another single variable is somewhat pointless, as we could have just applied the rules for B directly. That is the basic idea for how removing unit productions works: replace the unit production with a copy of all the productions for the righthand variable.
For example, consider this grammar:
S → Ab | A
A → aaA | ab
We remove the unit production S → A by simply copying A's productions into S's in place of the single A:
S → Ab | aaA | ab
A → aaA | ab
Note that we don't remove the productions for A as A might appear in other places in the grammar besides the removed unit production.
- Dealing with terminals and breaking up long productions — CNF needs all productions to have either exactly two variables or a single terminal on the right side. If we have productions like A → aBa, A → ab, or A → BCD that don't follow this form, then there are a couple of tricks for working with them.
The first trick for dealing with terminals is to turn them into variables. For instance, for a terminal a, we introduce a rule like X → a. Then we can turn something like A → aBa into A → XBX.
After doing the trick above with the terminals, we can then use another trick to break up long productions. If we have a production like A → BCD, we can introduce a new rule like Y → BC and then the production becomes A → YD. Longer productions can be broken up by repeated applications of this procedure.
Here is an example:
S → abAB
A → aA | a
B → aba | AB
First introduce the rules X → a and Y → b. Then the grammar becomes
S → XYAB
A → XA | a
B → XYX | AB
X → a
Y → b
Notice that we don't replace the production A → a with A → X because A → a is already in the right form for CNF. Next we need to break up the long productions S → XYAB and B → XYX. We can do this by introducing new variables V → XY and W → AB. Then we get the following:
S → VW
A → XA | a
B → VX | AB
X → a
Y → b
V → XY
W → AB
Useless Variables
Sometimes in the process of converting to CNF, useless variables can appear. A variable can be useless in either of the following ways:
- If there is no way to get to it. For instance, in the grammar below, there is no way to get to A, so A is useless.
S → aSb | λ
A → aA | a
- If it doesn't generate any strings in the language. One way this can happen is if the recursion never terminates, like below, where both B and C are useless.
A → B | C
B → B
C → cC
Useless variables can and should be removed from grammars.
A complete example
Here is a complete example, showing all the steps in action. Our grammar is the following:
S → ASA | Bb
A → aaA | ab | λ
B → bbbB | C
C → aA | B
First, the start variable S does appear on the right side of a production, so we create a new start variable S0 and a production leading from it to the old start variable:
S0 → S
S → ASA | Bb
A → aaA | ab | λ
B → bbbB | C
C → aA | B
Next we have the λ production A → λ to remove. This will affect the productions S → ASA, A → aaA, and C → aA. We do the process where we consider all the possible combinations that come from deleting A's. This yields the following:
S0 → S
S → ASA | AS | SA | S | Bb
A → aaA | aa | ab
B → bbbB | C
C → aA | a | b
As a result of the process above, we get the useless production S → S. We will delete it, so it won't appear in any following steps. Next, there are two unit productions to remove: S0 → S and B → C. We remove them by copying S's productions into S0 in place of S and by copying C's productions into B in place of C. See below.
S0 → ASA | AS | SA | Bb
S → ASA | AS | SA | Bb
A → aaA | aa | ab
B → bbbB | aA | a | b
C → aA | a | b
Notice that as a result of this process, the variable C is no longer reachable. It has become useless, so we will remove it. Next, let's deal with terminals by creating new rules X → a and Y → b. This gives the following:
S0 → ASA | AS | SA | BY
S → ASA | AS | SA | BY
A → XXA | XX | XY
B → YYYB | XA | a | b
X → a
Y → b
Finally, we have several long productions to break up. We can break them up by introducing the following rules: T → AS, U → XX, V → YY, and W → YB. This gives the following, our final grammar in CNF:
S0 → TA | AS | SA | BY
S → TA | AS | SA | BY
A → UA | XX | XY
B → VW | XA | a | b
X → a
Y → b
T → AS
U → XX
V → YY
W → YB
The process is long and tedious, and the resulting grammar is harder to understand, but the process is helpful in a few places, as we will see.
Pushdown Automata
Definition and Examples
A pushdown automaton (PDA) is an NFA that is given a stack to use for memory. A stack is a last-in-first-out data structure. The two operations we are allowed to do with a stack are to add an item to the top of the stack (push) and to remove item an item from the top of the stack (pop). A stack is like a stack of dishes in a cabinet, where clean dishes are put on the top of the stack and when you need a new dish, you always take from the top. The dish most recently put on the stack is the first to be taken off.
Giving an NFA some extra memory in this form gives it more power, as we will see. We will assume there is no limit to the size of the stack.
We will use the same type of state diagram to describe PDAs as we use for NFAs, except that the transitions will change. A typical transition will look like below:

There are three parts to it. The first part is just like in NFAs — it is the current input symbol being read. The second part tells us what symbol is currently on top of the stack. The third part tells us what operation to do to the stack. This will be one of three things: push, pop, or none, or possibly a combination of them. That is, we can push one or more symbols onto the stack, we can pop the top symbol from the stack, or we can do no operation (abbreviated as none).
So if the transition from q0 to q1 is 0, 1, pop, that means if we read a 0 from the input string and there is currently a 1 on top of the stack, then we will pop that 1 and move to State q1. Unlike with NFAs, there are two things that need to be true for this transition to apply: the current input symbol needs to be 0 and the top of the stack needs to be 1.
Sometimes for the second part of a transition, we will use the word “empty” to indicate that the stack is empty or we will use the word “any” to indicate we don't care what is on the stack. In other words, the transition applies no matter what the top of the stack is.
Like in an NFA, any transition that is not drawn is assumed to go to a junk state.
Note: There is no standard notation for PDAs that is common in computer science. Nearly every textbook on the subject seems to have their own notation. The notation we use here is a bit more informal than most other approaches.
Here is an example of a PDA that recognizes the nonregular language 0n1n with n ≥ 1.

State q0 is where we accumulate 0s from 0n1n and use the stack to remember them. Once we see a 1, we move to state q1. At that state, we read 1s and with each 1, we pop a 0 off the stack. If the stack becomes empty and we are done reading symbols, then we can move to the accepting state.
Here is a table showing the states of the machine and stack for the input 000111. In the third column, assume the stack top is at the right.
| symbol | state | resulting stack |
| (start of string) | q0 | empty |
| 0 | q0 | 0 |
| 0 | q0 | 00 |
| 0 | q0 | 000 |
| 1 | q1 | 00 |
| 1 | q1 | 0 |
| 1 | q1 | empty |
| (end of string) | q2 | empty |
Suppose now that we have the input string 10. Initially, we start in q0, but there is no transition from q0 with an input of 1. So we wind up in a junk state, and the string will not be accepted.
Let's look now at the input string 011. Initially at q0 we push a 0 onto the stack, and then we move to q1 and pop the 0, thus emptying the stack. We then have another 1 in our input string. We can't use the loop transition on q1 because it is of the form 1,0,pop which requires a 0 at the top of the stack. However, the stack is empty, so we can take the λ,empty,none transition to q2. But at state q2, there is no transition to deal with the remaining 1 in the input string, and we end up at a junk state. Thus the string is not accepted.
It's worth going through a few other example strings, like 001 or 0101 to convince yourself that this PDA really does accept 0n1n and only that.
Note that despite the λ, this machine is deterministic. There are no real choices between transitions to be made at any point. If we put a special symbol, like # at the end of the input, then we could replace the last transition with #,empty,none, and then the machine is very clearly deterministic.
Here is a small modification on the PDA above so that it accepts 0n12n, where there are twice as many 1s as 0s.

The only change is that with every 0 we read, we push 00 instead of 0. Getting a 1 still pops off only one 0, so we have to have twice as many 0s as 1s.
Here is a PDA for all strings of 0s and 1s with an equal number of both.

Here the stack holds both 0s and 1s. Whenever a 0 and a 1 meet, they annihilate each other. That is, if there is a 0 on the top of the stack and we read a 1, then we pop the 0. A similar thing happens if we read a 0 when there is a 1 on the stack. If the string has an equal number of 0s and 1s, then eventually everything will have canceled each other out and the stack will be empty. We can then move to the accepting state with the λ move. Note that moving there before the string is finished won't work since any further characters in the string will send us to the junk state from q1.
Here is a PDA for all palindromes that contain a # symbol in the middle. Examples include 001#100 and 1011#1101.

The approach here is at state q1, we push everything we read right onto the stack so that we can later compare these symbols to their counterparts in the second half of the string. When we see the # symbol, that tells us to move to the second half of the string, and we move to state q2. At that state we start comparing the current input symbol to the symbol on the stack. If they match, then we're good, and if not, then we implicitly head off to a junk state. At each point at this step, the current input symbol and the current stack top correspond to symbols that are equal distances from the center of the string.
If we want to change this PDA to accept any even-length palindrome, we can do so by making one small change. Replace the # symbol in the transition from q0 to q1 with a λ. This makes the machine nondeterministic. The machine nondeterministically “guesses” where the middle of the string is. Just like with NFAs, there is no actual guessing involved. Instead we imagine a tree of possible paths through the machine, and if any one of them accepts the string, then the string is considered to be accepted.
It can actually be shown that a nondeterministic PDA is needed for the language of palindromes. A deterministic machine won't work. So this is an area that PDAs differ from NFAs and DFAs. There is a procedure that converts any NFA to a DFA and vice-versa, so NFAs and DFAs are equivalent. In particular, there is nothing an NFA can do that can't also be done with a DFA. But some nondeterministic PDAs that can do things that deterministic PDAs can't.
Here is a PDA for all strings of the form 0n1k2n, with k,n ≥ 1.

This is similar to the 0n1n PDA but with an extra state. Here we need to match up the number of 0s to the number of 2s. The 1s in the middle don't have anything to do with that, so we don't bother with putting them on the stack. We use the stack only to remember how many 0s we get so that we can match them with the 2s at the end.
Here is a PDA for all strings of the form xy where x is a string of 0s and 1s, y is a string of 2s, and |x| = |y|. That is, the number of 2s equals the number of 0s and 1s combined, with the 0s and 1s coming before the 2s. Some examples are 0110122222 and 10112222.

For this PDA, as we encounter 0s and 1s in the first part of the string, we push an x onto the stack so we can count how many 0s and 1s we get. Then we use the stack at the next state to make sure that the number of x's on the stack matches the number of 2s in the string.
Here is a PDA that accepts all strings of the form 0k1n with k>n and n ≥ 1.

This is almost the same as the 0n1n PDA except that to guarantee more 0s than 1s, we should still have some 0s left on the stack when we reach the end of the input string.
How to approach creating PDAs
Let's look back at how to create a PDA for the language of strings of the form 0n1n with n ≥ 1. Imagine we were writing a program to tell if a string fits this form, and we have a stack to store things. We would scan across the string one character at a time. As long as we are seeing 0s, we push them onto the stack. Once we start seeing 1s, we start popping from the stack. When we are done seeing 1s, we check if the stack is empty. If it is, then the string is of the desired form. If it isn't or if anything else went wrong (like we got a 0 after seeing 1s or the stack emptied out before we were done getting 1s), then we know the string is not of the desired form. Here is some Python code to accomplish this.
string = '000111'
stack = []
i = 0
while string[i] ! = '1':
stack.append(0)
i + = 1
for j in range(i, len(string)):
if string[j] = = '1' and len(stack) > 0 and stack[-1] = = 0:
stack.pop()
else:
print('reject!')
break
else:
if stack = = []:
print('accept')
else:
print('reject!')
Below is the PDA again. The first state of the PDA corresponds to the first while loop, where we fill up the stack. The for loop in the middle corresponds to the second state, where we deal with 1s and pop from the stack. The first if statement in that loop corresponds to the loop transition at q1, where the character needs to be a 1 and the stack top needs to be 0. The else loop at the end that goes with the for loop uses a feature of Python where if we didn't break out of the loop early, then the code in the else loop runs. This corresponds to the third state in the PDA.

To create a PDA for a given language, think in terms of how you will make use of the stack. In the example above, we use it to remember how many 0s we saw in order to compare that to the number of 1s. The states of the PDA are for working on parts of the input string. Often, they correspond to control structures in programming languages, like loops or conditionals.
PDAs and Context-Free Grammars
There is a close relationship between PDAs and context-free grammars. If we are given a context-free grammar, we can create a PDA that accepts the same language as what the grammar generates. Here is an example demonstrating the process. The context-free grammar on the left generates the same language as the PDA on the right accepts.
In general, the construction always has exactly 3 states. It always starts with a λ transition that pushes the start variable onto the stack, and it always ends with a transition from the second state to the final state on an empty stack.
The middle state does all the work. To make things simpler, we assume that the grammar is in Chomsky Normal form, except that it's okay if the start variable appears on the right. In this middle state, there is a loop with transitions for each production.
A production like A → BC becomes a transition from the middle state to itself with the label λ,A,pop then push CB, where we pop A off the stack and then push C and B (in reverse order like this), so that B and C are on the stack in its place, with B being on top.
A production like A → a becomes a transition from the middle state to itself with the label a,A,pop where we simply pop A off the stack and do nothing else.
This three-state PDA simulates derivations from the grammar. For instance, picture a derivation like A ⇒ AB ⇒ aB ⇒ aBB ⇒ abB ⇒ abb. In doing this derivation, we start with the start variable A. Then we replace it with AB. Then A gets replaced with a and B gets replaced with BB, and finally both B's get replaced with b's. The input string abb will cause a similar thing to happen in the PDA. Initially the stack has an A on it. Then A on the stack is replaced with AB, just like in the derivation. Replacing A with a in the derivation corresponds to popping A from the stack. Then we replace the B on the stack with BB and finally we remove both B's from the stack as we read b's from the input string.
Converting PDAs to context-free grammars
It is also possible to go the other way, to find a context-free grammar that generates the same language as is accepted by a given PDA. However, the process is a bit tedious. Some books on this subject cover it, while others skip it. We will skip it here.
However, here is a very brief sketch of the process: First the PDA is transformed into one that has a single accepting state that only accepts on an empty stack. The PDA also needs to be transformed so that it only either pushes or pops a single symbol with each transition, and not both. Then for each pair of states p and q in the PDA, we create a grammar variable Ap,q and design productions so that Ap,q generates all strings that take the PDA from state p and an empty stack to state q and an empty stack. There are a couple of cases to consider in creating these productions.
The long and short of it is that PDAs and context-free grammars are equivalent, despite seeming so different. Any language that we can create a PDA to accept, we can also create a context-free grammar to generate, and the reverse is true as well. So in the same way that NFAs are equivalent to right-linear grammars, PDAs are equivalent to context-free grammars.
Non-Context-Free Languages
A context-free language is one that can be generated by a context-free grammar or PDA.**It's worth noting where the name context-free comes from. Every production in a context-free grammar has a single variable on the left side. Grammars in general can have more than one symbol on the left, as in aA → b. This says that if an A is preceded by an a, then we can replace that pair with a b. So what happens with A depends on the context it shows up in. In a context-free grammar, the context doesn't matter—the symbols around a variable have no effect on what that variable is replaced with.
Not every language is context-free. Two standard examples are 0n1n2n and the language of all words of the form ww, where the same word is repeated twice, like in 01100110 (where w = 0110).
Recall that 0n1n is context-free. A PDA for this language uses its stack to keep track of the 0s so that it can compare them to the 1s. However, a stack isn't powerful enough for us to be able to keep track of two things in 0n1n2n. Likewise, a stack is just the right data structure to recognize words of the form wwR (palindromes), but words of the form ww don't work so well with the LIFO property of the stack.
The primary technique for showing these languages and many others are not regular is the Context-Free Pumping Lemma. Recall the Regular Pumping Lemma, which says that if we have a long enough input string, then some state must be repeated as we trace the string through the automaton. That repeat means there is a loop, and that loop can be pumped up to create new strings in the language. If a language doesn't satisfy this pumping-up property, then it is not regular.
The Context-free Pumping Lemma is a little different from the regular language version. Suppose we are given a grammar in Chomsky Normal Form. Parsing a grammar in CNF is predictable, and the idea is if we have a long enough string, then somewhere in a parse tree for that string there will be a long path from the root to the end of the tree. That path will be longer than the number of variables in the grammar, which guarantees by the pigeonhole principle that some variable will be repeated on the path.
So if we trace from the edge of the tree back to the root, we will encounter a certain variable twice. Here is the key idea: take the subtree starting with the second occurrence (the one closer to the root of the tree) of the variable and paste it in place of the subtree starting at the first occurrence. This allows us to “pump up” the string to get a new string in the language generated by the grammar. Here is a demonstration of the process. We use the following grammar:
A → BC | AB | a
B → AA | CA | b
C → AB | c
Below is a parse tree for the string baacacab followed by the parse tree after the pasting process is done. We paste the circled subtree in for the bottom occurrence of C.
In the first parse tree above, we have broken the input string baaccaab into five parts: vwxyz. Notice how those parts also show up in the second parse tree, except that w and y are repeated. The pasting process has “pumped up” vwxyz into vw2xy2z. We could further repeat this pasting process to pump it up to vw3xy3z, or vwkxykz for any k ≥ 0, with k = 0 corresponding to completely deleting the lower subtree.
This can be formalized into the following:
Context-free Pumping Lemma. If L is a context-free language, then there is an integer n such that any string in L of length at least n can be broken into vwxyz with |wxy| ≤ n and |wy| > 0 such that vwkxykz is also in L for all k ≥ 0.
The restriction that |wxy| ≤ n says that the “loop” in the grammar can't take up too much of the string. The restriction |wy| > 0 is a fancy way of saying that w and y can't both be empty. One or both have to contain something. There is has to be something to pump up.
Just like with the Regular Pumping Lemma, we use this as a way to show a language is not context-free. Again, think of it as a game with the following gameplay:
- First, your opponent picks n.
- Then you pick a string s of length at least n that is in the language.
- Your opponent breaks s into vwxyz however they want, as long as the breakdown satisfies that |wxy| ≤ n and |wy| > 0.
- Then you show that no matter what breakdown they pick, there is a k ≥ 0 such that vwkxykz is not in the language.
Show that the set of all strings of the form 0n1n2n with n ≥ 0 is not a context-free language.
Let n be given. Choose s = 0n1n2n. Now suppose s is broken into vwxyz with |wxy| ≤ n and |wy| > 0. Because |wxy| ≤ n and s is composed of the strings 0n, 1n, and 2n, the string wxy is not long enough to contain all three symbols—0, 1, and 2. At most it can contain two of them. So since at least one of w and y is nonempty, the string vw2xy2z will contain n of one symbol and more than n of another symbol and hence cannot be in the language.
Note: We have to be careful here. Remember that we don't choose the breakdown ourselves; it is chosen by the opponent. We have to make sure our explanation covers all possible breakdowns that the opponent chooses. For n = 4, the string we choose is 000011112222. Here are some possible breakdowns the opponent can choose. Our explanation has to handle them all and then some.
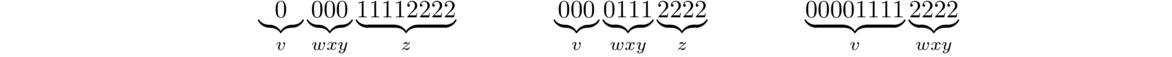
But the key idea is that wxy is limited to n symbols. In the examples above, this is a max of four symbols. It's easy to see then that there's no way for wxy to include all three types of symbols, so that when we pump up wxy into w2xy2, one or two of the symbol types will increase in number, while the third will stay fixed.
We see that the Context-free Pumping Lemma requires more work than the Regular Pumping Lemma. Having the string broken up into vwxyz with two parts being pumped up can lead to a lot more cases to consider.
The language consists of all strings that consist of the same string repeated twice. For example, the string 01100110 is of the form ww with w = 0110.
Let n be given. Set s = 0n1n0n1n. Now suppose s is broken up into vwxyz with |wxy| ≤ n and |wy| > 0. There are several possibilities.
First suppose wxy is completely contained in the left half of the string. If we take k = 0, the string vw0xy0z, which is vxz, consists of vwxyz with some, but no more than n, symbols removed from its first half. The removal of these symbols forces part, but not all, of the second 0n group to now be in the first half of the string. This means that the first half will end with a 0. But the second half will still end with a 1, so this string cannot be of the proper form.
A similar argument holds if wxy is contained in the right half, and a similar argument works if wxy extends across both halves of the string but one of w and y is empty. The only remaining case is if w is in one half of the string and y is in the other. If |w| > |y|, then the second half of vw2xy2z will start with 1s, which is a problem since the first half starts with 0s. A similar problem happens if |w| < |y|. Finally, suppose |w| = |y|. In that case, the vw2xy2z will be of the form 0n1m0m1n with m ≠ n, which is not of the proper form.
Suppose we try to use the Context-free Pumping Lemma to show that the language 0n1n is not context-free. Given n, suppose we choose s = 0n1n. It turns out there is a breakdown the opponent can use that such that vwkxykz is in the language no matter what.
If they choose w to be the last 0, x to be empty, y to be the first 1, and set v and z to be whatever is left over on either side, then when we pump up, the number of 0s and 1s stays equal. For instance, with n = 4, our string is 00001111 and the opponent has chosen this breakdown:

Pumping this into vwkxykz adds the same number of 0s as it adds 1s.
If we had tried to write a proof for this and neglected this possible breakdown, we would be led to an incorrect conclusion.
Closure Properties
Recall that regular languages are closed under various operations like union, intersection, complements, concatenation, and the star operation, among other things. This means that if we can build an NFA (or DFA or regex) to accept language L and an NFA to accept language M, then we can build one for L ∪ M, L ∩ M, etc.
We saw various constructions in Section 2.5 for how to combine NFAs to do this.
Context-free languages are closed under some of these operations, but not others. And it matters whether we are looking at deterministic context-free languages (DCFLs) or general context-free languages (CFLs), which may or may not be deterministic.
Of the operations listed above, DCFLs are only closed under complements. The same process of flip-flopping the accepting and non-accepting states that works for complementing a DFA works for deterministic PDAs. However, because acceptance in a non-deterministic machine is complicated, the process doesn't work for CFLs in general. For NFAs, we could convert the NFA to a DFA and then complement it, but there is no general process for converting a non-deterministic PDA into a deterministic one.
CFLs in general are closed under unions, concatenations, and the star operation, but not intersection. The same NFA constructions from Section 2.5 work for PDAs. We can also use grammars for this.
For example, suppose we have grammars for languages L and M. Say L's grammar has variables A1, A2, etc. and M's grammar has variables B1, B2, etc., with A1 and B1 being the starting variables. Then we have the following:
- A grammar for L ∪ M would have the starting production S → A1 | B1, along with all the productions from the two grammars.
- A grammar for LM would have the starting production S → A1B1, along with all the productions from the two grammars.
- A grammar for L* would have the starting production S → SA1 | λ, along with all the production's from L's grammar.
As noted above, the intersection of two CFLs is not necessarily a CFL. The standard example of this is as follows: Let L be the language 0n1n2m, where the numbers of 0s and 1s match, and there can be any number of 2s. And let M be the language 0m1n2n, where the numbers of 1s and 2s match, and there can be any number of 0s. What these two languages have in common is precisely the language 0n1n2n, with equal numbers of all three symbols. This language is not context-free, as we showed earlier with the pumping lemma.
Other questions
People are also interested in other questions about context-free grammars, such as the following:
- Does the grammar generate anything at all?
- Does the grammar generate all possible strings?
- Is it ambiguous?
- Given another grammar, does it generate any strings in common with this one?
- Given another grammar, does it generate the same set of strings as this one?
Except for the first question, these questions are all unanswerable in general. We can answer them in special cases, but there is no general algorithm for answering them. We will see why later.
Turing Machines
Introduction
We have built DFAs and PDAs to recognize many types of languages, but as we've seen each has its limitations. We now come to a type of machine, a Turing Machine, that is much more powerful.
Let's quickly review DFAs. Consider the DFA below.

We feed this machine an input string like 0110. We can think of the DFA as consisting of two parts: the state machine (shown above on the left), that acts as the main processor, and an input unit (shown above on the right) with a read head that scans left to right across a tape one symbol at a time, feeding those symbols into the state machine.
A Turing Machine is very similar, except that its input unit is more powerful. In a DFA, the tape can only move to the right and is read-only; in a Turing Machine it is allowed to move left or right and it can overwrite things on the tape. In particular, here are the key features of a Turing Machine:
- The input unit contains a tape and a read head. The tape has a definite left end, but no right end (it is infinite). The read head is allowed to move left and right across the tape.
- There is a finite alphabet of symbols that can be written to the tape, along with a special blank symbol, ⊔, that indicates an empty tape cell.
- Transitions in the control unit are shown like below:
The first symbol on the transition specifies what is on the tape at the current read head location. The second symbol specifies what symbol to overwrite at that tape location. The third specifies whether to move the read head left or right after writing.
- There is a single accept state. Unlike other automata, when a Turing Machine gets to this state, it immediately stops (halts) and does no further actions.
- Any transition that is not drawn is assumed to go to a junk state. In this situation, the machine automatically stops (halts) and rejects the input string.
- For now, we will assume our Turing Machines are deterministic, where there is never a choice as to which transition to take.
Here is an example Turing Machine that accepts the language of all strings of the form 0*.

Here is the basic idea behind this machine: Each time we read a 0, we write a 0 (i.e., the tape contents don't change since there already is a 0 there), and move the read head right. If we ever see a nonzero value, there is no transition for that, and the machine automatically rejects the string. If we reach the end of the input, we will see a blank symbol (⊔). When we see that, we know we're good and we move to the accepting state.
Here is a diagram showing how everything progresses on the input string 00.

The read head starts at the left end of the string. We read a 0, overwrite a 0, and move the read head right, staying in state q0. We see another 0 and do the same thing. Next, we see a blank symbol. This tells us to move to the accepting state q1. So the string is accepted, and the machine halts.
On the other hand, if we had the input string 100, then initially we would read a 1, see no transition specified for that situation and immediately halt and reject the string.
Online Turing Machine simulators
To really see how a Turing Machine works, find a simulator online that animates the action of the machine. A particularly good one is at https://turingmachinesimulator.com.
Examples
- A Turing Machine for all strings of 0s and 1s with at least two 0s.

The language in question is regular, so we can build a DFA for it. We can convert it to a Turing Machine by basically leaving the tape alone and always moving right. This sort of thing works to turn any DFA into a Turing Machine.
- A Turing Machine for all strings of the form 0n1n.
This is not a regular language; we need to move in both directions on the tape and overwrite cells.
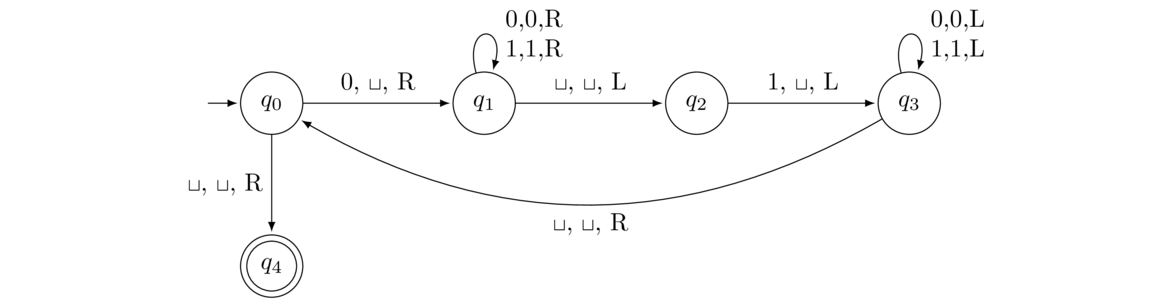
A diagram like this can be a little overwhelming to understand at first glance. Behind the diagram there lies a simple strategy. We start by erasing the first 0. Then we scan right until we get to the last 1 and erase it. Then we scan back left and erase the first 0, and we keep scanning back and forth, erasing symbols until there's nothing left. If we get to that point, then we accept the string. Here are the first several moves of the machine on the input string 000111:



At this point it starts scanning left again at state q3 until it reaches the left end of the tape (indicated by a blank). It uses the blanks at either end to know when to turn around. We continue scanning back and forth until there is nothing left on the tape but blanks. We recognize this situation at state q0 if we see only a blank as we try to move right.
If at any point we get something we don't expect, the machine crashes and rejects the string. For instance, for the input string 00110, the machine erases the first 0 and then scans right until it reaches the right end. At this point it expects a 1, but it sees a 0, has no transition for that case, and crashes.
Looking state-by-state, at q0, we look for a 0 at the start of the string and erase it. The job of q1 is to move all the way to the right of the string without changing the tape. When we reach the end, we move to q2, where we erase a 1 at the end. The job of q3 is to move all the way to the left of the string without changing the tape.
Use the following “program” to test this out at https://turingmachinesimulator.com. That simulator animates the motion of the read head, making it very clear how the machine works.
name: 0^n1^n init: q0 accept: q4 q0,0 q1,_,> q0,_ q4,_,> q1,0 q1,0,> q1,1 q1,1,> q1,_ q2,_,< q2,1 q3,_,< q3,0 q3,0,< q3,1 q3,1,< q3,_ q0,_,>
- A Turing Machine for all strings of the form 0n1n2n.
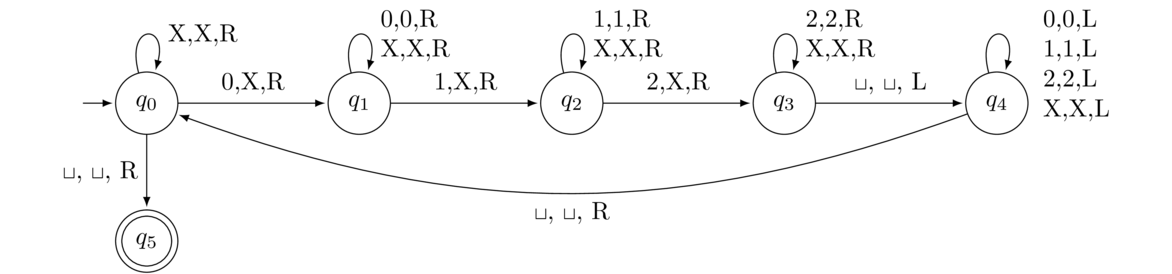
The strategy we used in the last problem of erasing symbols will lead us to some difficulty. Instead of erasing them, we can mark them with an X to indicate they have been read. What we do here is scan left to right and mark the first 0 we see with an X, then mark the first 1 with an X, and then mark the first 2 with an X. We keep going right until we reach the end of the string, then turn around and go all the way back to the start and repeat. For simplicity, we will assume that there is a blank that marks the start of the tape so that we can find the front of the string. We will see in Example 5 that this is okay. We keep scanning through, replacing one 0, 1, and 2 with an X on each scan. We then need to recognize when to accept. Once we've replaced the last 2, we scan to the end of the string, then go back to the start. From there, if all we see are Xs until we reach the end, then we accept.
Note that this language is impossible to do with a PDA, so we have an example here of something a Turing Machine can do that a PDA can't. Note also that it's not too hard to simulate a PDA with a Turing Machine. We can use part of the tape to hold data just like a PDA's stack. Thus Turing Machines are more powerful than PDAs, as they can do anything a PDA can do, and more.
- A Turing Machine for palindromes in {0,1}.
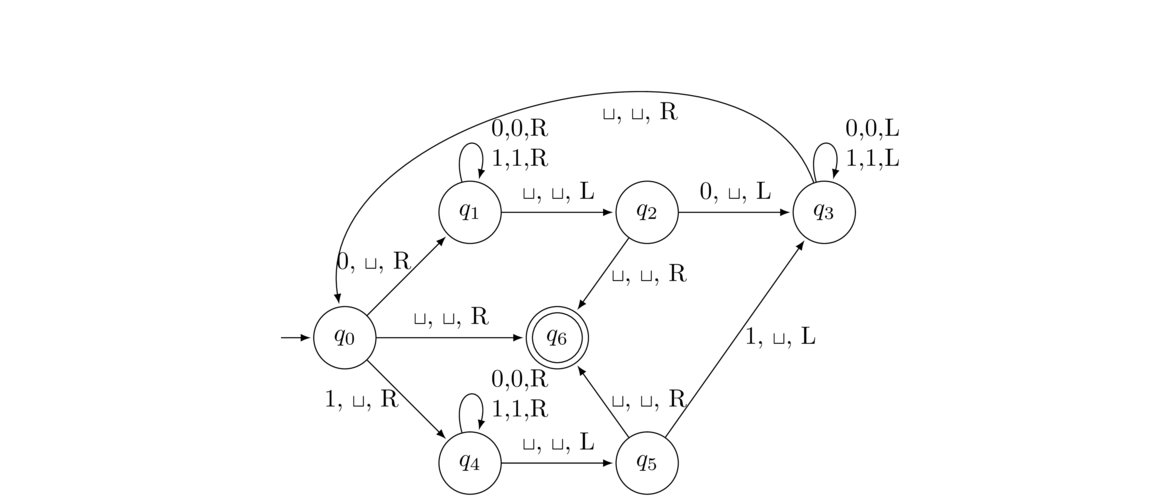
Consider a palindrome like 0010100. Notice how the first and last symbols must match, as must the second and second-to-last, etc. This suggests that our Turing Machine look at the first character, erase it, scan to the right until the end of the string, and compare the last to the first. Then it can move back to the left and repeat the process.
The trick is how to get the machine to remember what the first symbol is in order to compare it with the last. We use states of the control unit for this. From the first state, we branch off (sort of like an if statement) based on whether we see a 0 or a 1, and each branch will then make the appropriate comparison at the end.
The only other trick is that palindromes come in odd and even varieties. For even palindromes, like 0110, we will end up erasing all the symbols. For odd palindromes like 010, we will have an unmatched symbol (the middle one) left over. We can handle both cases by seeing if the current tape symbol is blank at states q0, q2, or q5.
- A Turing Machine that shifts every symbol over one spot and adds the symbol # at the start.
The idea of this is that Turing Machines can do more than just accept or reject strings. And this operation is useful as a subroutine in more complex Turing Machine operations.
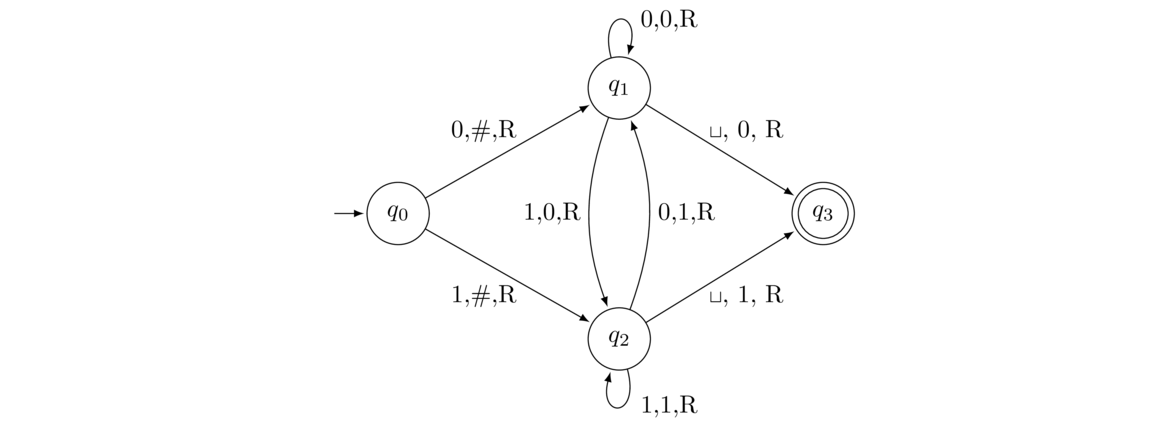
The strategy here is to overwrite the current tape symbol with # initially and with the most recently read tape symbol after that, using the states of the machine to “remember” what that symbol is.
- A Turing Machine to do an XOR operation.
Below is a Turing Machine that takes two equal-length binary strings separated by a # character, does the exclusive OR (XOR) operation on them, and outputs the result at the end of the tape.
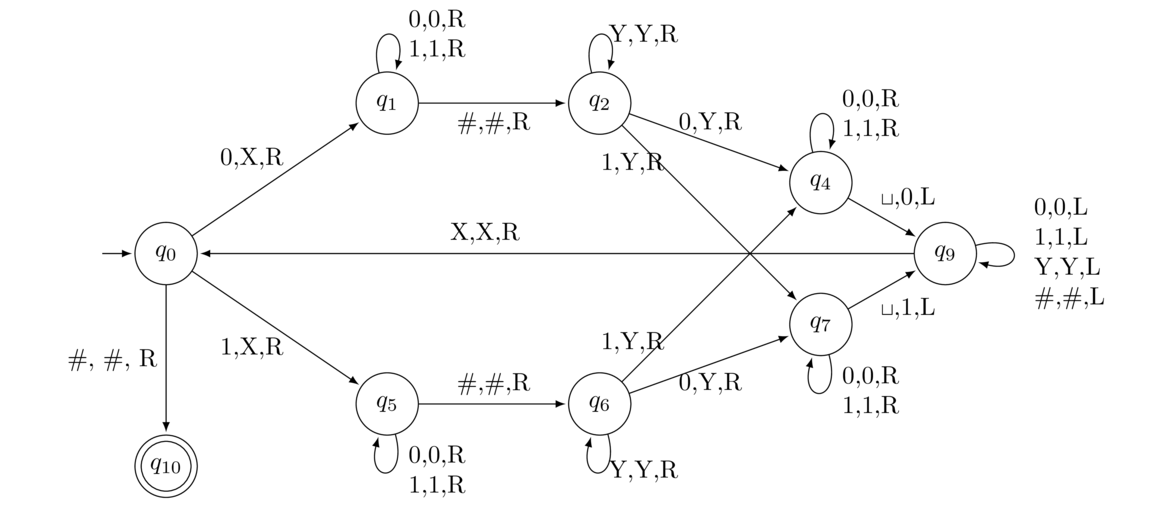
The idea behind this Turing Machine is we look at the first symbol on the left of the # symbol, then look at the first symbol on the right of the #, XOR them, and store the result at the end of the tape. We repeat this for each pair of symbols on either side of the # symbol. As we read symbols on the left, we mark them with an X to indicate we are done with them, and as we read symbols on the right, we mark them with a Y.
State q0 has a branch to remember if we saw a 0 or a 1 on the left side. States q1 and q2 move the tape right until we get to the next symbol on the right of the #. States q5 and q6 play a similar role, just for the other branch. At q2 and q4 we have another branch, this time to deal with whether the character on the right of the # is 0 or 1. States q4 and q7 move to the end of the tape and write either a 0 or a 1. State q4 is specifically for writing a 0, if the symbols on either side of # are both 0 or both 1. State q4 is for writing a 1, if the symbols on either side are 0 and 1 or 1 and 0. State q9 moves all the way left until it hits an X, indicating that we are ready for the next symbol on the left of the # symbol. If there is nothing more to be read at this point, then we will see the # symbol, and that's when we accept.
One downside of this machine is it destroys the two strings being XOR-ed. There are a couple of ways around it. One is to copy them elsewhere on the tape. Another is to overwrite 0s and 1s with different things, instead of always just X's on the left and Y's on the right. Then, when we're done with the XOR, we can go back and change them to what they originally were.
We will stop here with building complete Turing Machines. The last example shows we can perform an XOR operation, an instruction commonly found in CPUs. It's not much more work to show how Turing Machines can do other logical operations, as well as binary addition and subtraction. The example before this showed how a Turing Machine can move things around the tape. Combining logical operations along with the ability to move things allows a Turing Machine to act just like a modern CPU, just a lot slower. We can combine these operations to much more complex tasks. Building state diagrams for these things can get very tedious, and the resulting Turing Machines can be very large. But in principle, once we have Turing Machines for all these primitive operations, we can combine them to build a computer capable of computing anything that an ordinary computer can compute.
So a Turing Machine is essentially a very simple device that is capable of performing any type of computation that a real computer can do. Turing Machines can compute prime numbers, Fibonacci numbers, and even do your taxes.
The appeal of Turing Machines is that we are interested in how simple a device can be that is capable of doing anything a real computer can do. Turing Machines are particularly simple in that they consist only of a tape, a read head that can move back and forth and write symbols, and a control unit with a finite number of rules. This is enough in theory (it seems) to compute anything that can be computed.
Formal Definition and Further Details
It's worth going through the formal definition of a Turing Machine. The definition contains seven parts:
- Q — A finite set of states
- Σ — A finite alphabet for the input string (note that ⊔ is not a symbol in this alphabet)
- γ — A finite alphabet of symbols that can be written on the tape
- q0 — A single start state
- qa — A single accept state
- qr — A single reject (junk) state
- δ — A transition function of the form δ: Q × γ → Q × γ × {L,R}. That is, δ takes as arguments a current state and tape symbol and outputs a new state, a new symbol to write on the tape, and whether to move the tape head left or right.
A string is considered to be accepted if a sequence of transitions starting with the start state and initial symbol on the tape eventually puts the machine into the accept state. A string is rejected if such a sequence of transitions puts the machine into the reject state. In our state diagrams, to keep things simple, we don't show the reject state or the transitions into it. All transitions that are not specified are assumed to go to the reject state.
Here are a few important notes about the definition:
- There are finite numbers of states and symbols in the alphabet.
- The tape is infinite. This makes Turing Machines a little unrealistic. However, it turns out you have to work pretty hard to find something practical that can't be done with a finite tape.
- Authors don't seem to agree on a standard definition for Turing Machines. Some authors allow the tape to be infinite in both directions. Others allow the read head to have a stay-put option. Still others allow multiple accepting and rejecting states. We will see that none of these affect the overall power of the machine in terms of what it can and can't compute.
- Turing Machines were invented by Alan Turing in 1936, a few years before the first computers were designed and built. Around the same time, Alonzo Church developed a different model of computation, the lambda calculus, that turns out to be equivalent to Turing Machines.
The Church-Turing thesis
The Church-Turing thesis roughly says that anything that can be computed can be computed by a Turing Machine. Another way of saying it is that anything that can be computed by a human working with a pen and paper and unlimited resources can be computed by a Turing Machine.
It is a “thesis” and not a theorem because it can't be proved. The statement is not precise enough. Essentially, it says that our intuitive notion of an algorithm is captured by Turing Machines.
No one has yet found anything that can be done by an algorithmic process that can't be done on a Turing Machine.
Modifications to Turing Machines
As evidence in favor the Church-Turing Thesis, we will try to add power to our Turing Machine and show that the resulting machines can't do anything that an ordinary Turing Machine can't do.
- Turing Machines with a stay-put option
Here instead of the read head having to move left or right with each transition, we also allow it to stay in place. For simplicity, suppose the only symbols are 0, 1, and ⊔. Then a stay-put transition like the one on the left can be replaced with two ordinary transitions, as shown on the right.

In short, we replace a stay-put move with a right move followed by a left move. The left move is designed to not modify the tape at all. In general, we can take any Turing Machine with a stay-put option and convert it to an ordinary Turing Machine by transforming the stay-put moves as shown above. Thus, the stay-put option may make Turing Machine “programs” a little simpler, but it doesn't add any new power to Turing Machines.
- Turing Machines with a bi-infinite tape
We initially defined a Turing Machine's tape as being infinite in one direction only. Let's consider a tape that is infinite in both directions.
A portion of a bi-infinite tape is shown below on the left. The numbers in the cells are the cells' indices. We convert it to an ordinary tape as shown below on the right. The first tape symbol is a special character, the next symbol the bi-infinite tape's cell 0, and following that are the cells at indices 1, -1, 2, -2, etc.

It's not enough to construct the tape. Transitions are also affected. A move one cell to the right in the bi-infinite machine initially corresponds to a move of two cells to the right in the standard machine. And a left move corresponds to a move two cells left.
However, there is a trick. Let's say we're at cell 0 in the bi-infinite machine and we move left. That takes us to cell -1, but a move of two cells left in the standard machine would send us off the edge of the tape. That's the purpose of the special # character. When we hit that, we change things around so that now a left move on the bi-infinite tape would correspond to two right moves in the standard machine. Likewise, a right move corresponds to two left moves. In general, any time we hit the special # symbol, we flip-flop things like this.
In short, this process shows that anything that the bi-infinite tape machine can do can also be converted into something on a standard Turing Machine. So a machine with a bi-infinite tape is no more powerful than a standard Turing Machine.
- Multiple tapes
Here we consider a Turing Machine that has multiple tapes, each with its own read head. We show how to convert such a machine into an ordinary Turing Machine. Here is an example with three tapes.

Below is the how we convert it to a single tape.

We place the tapes next to each other on the single tape with a special character (#) to separate the tapes. Though each of the tapes are infinite, they only have a finite amount of non-blank symbols at any point in time. To indicate where the read heads are on each of the tapes, we replace each symbol that a read head is pointing to with a dotted version of itself. These dotted symbols are extra symbols that we add to the tape alphabet.
Now let's talk about how transitions work in the single-tape machine. Suppose we have the following transition in the three-tape machine, where the operations for the various tapes are separated by vertical bars.
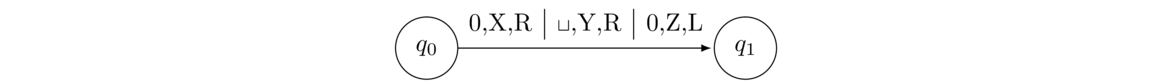
The way we handle this is to start with the read head of the ordinary TM all the way at the left. It then scans right until it reaches a dotted symbol. Then it performs the tape 1 transition and modifies the first portion of the tape, changing which symbol is dotted to indicate where the read head has moved on tape 1. Then it scans right for the next dotted symbol and performs the tape 2 transition.
It does this for all the tapes and then repositions the read head at the start of the tape for the next step. If any of the individual tape operations causes a tape to use more space than it has on the single-tape machine, we shift everything on the single-tape machine to the right over by one unit to make room. This will occur if we end up trying to make one of the # symbols dotted. Here is what the tape would look like after the transition above:

Though it wouldn't be terribly difficult to give a state diagram for this single-tape machine, it would be fairly long and tedious, so we won't do it here.
When trying to build a Turing Machine for things that are fairly complicated, it is often easier to use a multi-tape Turing Machine. In fact, we will do that in the next example.
- Nondeterministic Turing Machines
A nondeterministic Turing Machine is one where the machine has a choice of which transition to take, as shown below.

In this example, if we are in state q0 and we see a 0 on the tape at the current read head location, we can stay at q0 or move to q1.
Just like with DFAs, in a deterministic Turing machine, there is a definite, predictable sequence of states that the machine will pass through. Every time we run the machine, it will pass through the exact same sequence of states and perform the exact same tape operations.
With an a nondeterministic machine, we can think of things more like a tree diagram, where each potential choice creates a new branch. A string is accepted by a nondeterministic machine if there is some path through that tree that leads to an accepting state. We can image that the nondeterministic machine tries all possible paths and determines if one of them is accepting. See the figure below for a few levels of such a tree.

It seems like this might give a nondeterministic Turing Machine more power than an ordinary Turing Machine. In one sense it does: being able to try all possibilities in parallel can give it an exponential speedup over an ordinary machine. But in an other sense, it doesn't: there is nothing that a nondeterministic Turing Machine can compute that an ordinary machine can't also compute.
To see why, we show how to convert a nondeterministic Turing Machine into a deterministic one. We do this by having the deterministic machine run a breadth-first search of the tree of all possible paths through the deterministic machine. To do this, we use three tapes. The first tape holds the input string. The second tape keeps track of where we are at in terms of the breadth first search. The third tape runs the simulation of the current path being tried on the nondeterministic machine.
To be a little more specific, let b be the maximum number of branches there are in the tree. Specifically, it's the maximum number of choices there are at any given state in the nondeterministic machine. Then we label each of the nodes at distance 1 from the tree's root as 1, 2, 3, … b; the nodes at distance 2 will be 11, 12, 13, … bb; and nodes at higher distances are labeled similarly.
The second tape of the deterministic machine stores the current one of these labels that we are working on. We use these labels when running the simulation of the nondeterministic machine on tape 3. A label like 231 tells us to take choice 2 at the first step, choice 3 at the second step, and choice 1 at the third step. We then check to see if that sequence put us into an accepting state or not. Note that not all of these labels will correspond to actual paths in the tree, as there will likely not be b choices at every node. We ignore the ones that don't correspond to actual paths.
A few notes:
- We will see shortly that Turing Machines can get caught in infinite loops, so a depth-first search could not be used in place of a breadth-first search, as the DFS could disappear down a never-ending path.
- DFAs and NFAs are equivalent, as we can convert any NFA to a DFA. And now we see that nondeterministic Turing machines are equivalent to deterministic ones. However, PDAs are a different story. There are some things that a nondeterministic PDA can do (like palindromes) that a deterministic one can't do. So sometimes nondeterminism adds extra power and sometimes it doesn't.
Things Equivalent to a Turing Machine
Here are a few things that are equivalent to a Turing Machine.
- A Turing Machine whose tape alphabet consists of two symbols and the blank symbol
We don't actually need a large alphabet. A Turing Machine with a binary alphabet and the blank symbol is just as powerful as an ordinary Turing Machine. The drawback is that to deal with not having so many symbols to work with, the state diagrams will have to be bigger.
- DFA + queue
A PDA is a DFA with an unbounded stack to use as memory. We have seen that PDAs can do things that DFAs can't, but there are things that PDAs can't do, like accept the language 0n1n2n.
However, if we replace the stack with a queue, then the resulting automaton is as powerful as a Turing Machine. That is, we can use this type of automaton to simulate a Turing Machine, and we can use a Turing Machine to simulate this type of automaton.
What is it about queues that makes them more useful than stacks here? With a stack, we only ever have access to the top item. If we need to get an item in the middle of the stack, we have to throw away all the items on top to get to it, and we have nowhere to put those items we toss away.
However, with a queue, if we want access to a middle item, we can keep removing things from the front of the queue and putting them at the end of the queue, essentially shifting things over until we get to that middle item. So we don't ever have to lose things like we would with a stack. So we can use a queue in a way that is somewhat analogous to a Turing Machine's tape.
- DFA + 2 stacks
A queue can be implemented with two stacks. This is a common exercise in Data Structures textbooks. Recall the problem mentioned above about stacks: to get access to the middle items, we have to throw away the top items. But if we have a second stack to hold those top items, then we don't have to lose them.
- Unrestricted grammars
All the grammars we have seen so far are context-free grammars, where all productions have a single variable on the left side, like in A → Bb | aaa. A more general type of grammar, called an unrestricted grammar, has productions of the form x → y, where x and y can be any strings of variables and terminals, with the one exception that x can't be λ.
So now we are allowed productions like aAb → bbA. This says that any time we see an A surrounded by a and b, we can replace it with bbA. Unrestricted grammars allow us to do things we couldn't do with context-free grammars. For instance, here is a grammar for all strings of the form anbncn:
S → aAbc | abc | λ
Ab → bA
Ac → Bbcc
bB → Bb
aB → aaA | aa
To understand how this works, let's try deriving the string aaabbbccc. It's a long derivation, but watch how the A and B variables move back and forth generating new terminals.
S ⇒ aAbc ⇒ abAc ⇒ abBbcc ⇒ aBbbcc ⇒ aaAbbcc ⇒ aabAbcc ⇒ aabbAcc ⇒ aabbBbccc ⇒ aabBbbccc ⇒ aaBbbbccc ⇒ aaabbbccc
The A and B symbols move back and forth in a way that is reminiscent of how a Turing Machine operates. We won't prove here that unrestricted grammars and Turing Machines are equivalent, but hopefully this examples gives you a sense of how that might be proved.
As another example, here is a grammar for all strings of a's, b's, and c's with equal numbers of each symbol.
S → SABC | λ
AB → BA
BA → AB
AC → CA
CA → AC
BC → CB
CB → BC
A → a
B → b
C → c
The first production lets us generate however many A's, B's, and C's as we need, and the middle productions allow us to rearrange them into whatever order we want.
Turing completeness
Something is called Turing complete if it is possible to use it to implement a Turing Machine. For instance, every popular programming language is Turing complete. In fact, it's a nice exercise to try to implement a Turing Machine in a programming language.
There are some other systems that are surprisingly Turing complete. For instance, the card game Magic: the Gathering has a system of rules that is sufficiently complex that it's possible to use them to construct a Turing Machine. Other games that are Turing Complete include Minecraft, Pokemon Yellow, and Super Mario World. Even the rules of non-programming languages like CSS and SQL are enough to implement a Turing Machine. See http://beza1e1.tuxen.de/articles/accidentally_turing_complete.html for more.
Things not equivalent to a Turing Machine
Turing Machines are designed to be relatively minimalistic in terms of not having a lot of components but being able to compute essentially anything that is computable. We saw earlier that if we take away a little bit from a Turing Machine by restricting it to a binary alphabet, then the resulting machine is still as powerful as an ordinary Turing Machine.
But there are certain things we can't take away. Namely, we can't take away its ability to move both left and right or its ability to rewrite things on the tape. A Turing Machine that can only move right can be shown equivalent to a DFA, as can a Turing Machine that can scan left and right but not modify the tape.
A very practical concern is the fact that a Turing Machine has an infinite tape. This means that we cannot build a true Turing Machine in real life. What happens if we restrict it to having a finite tape?
One thing we can do is restrict a Turing Machine's tape so that it is no longer than the input string's length. This type of machine is called a linear bounded automaton (LBA). LBAs are a more practical model of real physical computers than Turing Machines. We can give LBAs a little more flexibility by allowing the tape length to be a multiple of the input string length. It has been proven that this doesn't give LBAs any more power in terms of what they can and can't compute.
It seems like having a finite tape might seriously hamper an LBA's abilities, but in terms of practical problems, not so much. There are things that a Turing Machine can do that an LBA can't do, but we have to work pretty hard to find them. One example is the problem of determining if two regular expressions accept the same language.
LBAs are equivalent to a special type of grammar called a context-sensitive grammar. This is a grammar where all productions are of the form x → y, where x and y are strings of variables and terminals with the restriction that |x| ≤ |y|.
Enumerators and Universal Turing Machines
Enumerators
Turing's original conception of Turing Machines was as enumerators. Instead of taking strings and telling us whether they are or aren't in a language, Turing's original machines would output all the strings in the language one-by-one onto the tape. It can be shown that these two conceptions are equivalent.
Universal Turing Machines
A Universal Turing Machine (UTM) is a Turing Machine that can simulate other Turing Machines. The inputs to a UTM are a Turing Machine M and a string w, and the result is whatever the result of M is when run with input string w.
Inputs to Turing Machines are strings, so we have a little work to do if we want to use a Turing Machine as input to another Turing Machine. The trick is to find a way to represent Turing Machines as strings. Until now, we have represented our Turing Machines with state diagrams. We can turn this diagram into a string in any number of different ways. The “program” given earlier for the online Turing Machine simulator is one such string representation. If we like, we can convert the representation to pure binary.
There are a number of ways to construct a UTM. Here is a simple way using three tapes: Tape 1 contains the string representation of the input Turing Machine M. Tape 2 is the tape used by M. Tape 3 keeps track of what state M is currently in.
This idea of one object simulating versions of itself comes up often in computer science. Virtual machines and emulation are two examples. Another example is how the compiler for many programming languages is often written in the language itself.
Undecidability
Recursive and Recursively Enumerable Languages
In this chapter, we consider what Turing Machines can't do. If the Church-Turing thesis is true, then whatever a Turing Machine can't do is something that no computing machine can do. So we are investigating the limits of what can and cannot be computed. First, though, we have a couple of important notes about Turing Machines.
DFAs and PDAs always have two possible outputs: accept or reject. With Turing Machines, there is a third possibility: an infinite loop. Just like programs we write can (accidentally) get caught in an infinite loop, so can Turing Machines. Here is an example that gets caught in an infinite loop with the input string 01.

People usually use the term halt to refer to the case when a Turing Machine accepts or rejects a string, as the machine stops running in that case. When a Turing Machine infinite loops, it never stops and we never get an accept or reject answer.
We mentioned this earlier, but just to reiterate—every Turing Machine can be represented by a string. There are many ways to do this, but the key thing to remember is that it can be done. This allows us to use Turing Machines as inputs to other Turing Machines. Often we just say that we input a Turing Machine M into another Turing Machine. What we mean is that we input a string representation of M into the Turing Machine.
There are two important definitions about the kinds of languages that Turing Machines accept:
- Recursive Languages — A language is called recursive or decidable if there exists a Turing Machine that gives a definite accept or reject answer for every possible input string.
- Recursively-enumerable — A language is recursively enumerable or recognizable if there exists a Turing Machine that gives a definite accept answer for every input string that is in the language. If an input string is not in the language, the machine could either reject the string or get caught in an infinite loop.
In short, with recursive languages, we always get a definite yes or no answer. With recursively enumerable languages, we can always get a definite yes answer, but we are not guaranteed a definite no answer.
In particular, every recursive (decidable) language is also recursively enumerable (recognizable).
Note: Some people prefer the terms recursive/recursively enumerable, while others prefer decidable/recognizable. It seems to be a fairly even split as to how often each is used.
Here are a few examples:
- The language of all strings of the form 0n1n2n is recursive (decidable). In Section 6.2, we built a Turing Machine for this language. We could go through and formally prove that this machine always gives the right answer and never gets caught in an infinite loop.
- The language consisting of all Turing Machines that accept the empty string is a recursively enumerable language. The strings of this language are string representations of Turing Machines that accept the empty string. To show the language is recursively enumerable, we can build a Universal Turing Machine that takes a Turing Machine M as an input, runs it with input λ, and if M accepts λ, the UTM will eventually tell us so. However, if M doesn't accept λ, then there is no guarantee that our UTM will give us an answer, as M could get caught in an infinite loop. We just can't tell the difference between whether it is taking a while to reject or if it is stuck in an infinite loop. To just reiterate: If M accepts λ, we will eventually get an answer. But if M doesn't accept λ, then it's possible we might never get an answer, as the machine could infinite loop. And it does turn out that this language is not recursive, though we are not yet ready to show that.
Earlier, we mentioned that Turing's original conception of his eponymous machine was as an enumerator, one that would output a list of all the strings in the language. That word “enumerator” is where “enumerable” comes from in “recursively enumerable”. In particular, a language is recursively enumerable if and only if there is an enumerator for it. Here is why:
Think of the enumerator as a “lister” and the TM that satisfies the definition of recursively enumerable as a “yes-checker”. Given one, we need to show how to build the other.
Given a lister, we build a yes-checker just by making a Turing Machine that scans the lister's list from left to right, looking for the input string. If it's there, it will eventually find it and accept, so we get a definite yes answer. If it's not there, it will get caught scanning forever and not find it.
Given a yes-checker, we could try to build a lister by testing strings in order by length. For instance, if the alphabet is {0,1}, then the order would be λ, 0, 1, 00, 01, 10, 11, 000, etc. Then for each of these, we run it on the yes-checker, and if we get a yes answer, then we add the string to our list. However, since our yes-checker can't give us a definite no answer, we could get stuck in an infinite loop. For instance, if 10 is not in the language, then we might never get past that string. This would be bad. Instead a nice trick called dovetailing is used. The idea is as follows: Let s1, s2, … be all the strings in Σ*, listed out in length order. For Σ = {0,1}, this might be s1 = λ, s2 = 0, s3 = 1, s4 = 00, etc. Then do the following:
- Step 1: Run s1 for 1 step on the Turing Machine. If it accepts, write s1 onto the output tape.
- Step 2: Run s1 and s2 for 2 steps each on the Turing Machine. If s1 or s2 is accepted, write it on the output tape.
- Step 3: Run s1, s2, and s3, for 3 steps each on the Turing Machine. Write any that are accepted on the output tape.
Keep going with the Steps 4, 5, etc. in the analogous way. This is a bit inefficient, as any string that is accepted will appear many times on the tape, but it does avoid the problem of infinite loops, and it does guarantee that every accepted string will appear on the output tape.
The families of languages we've seen — regular, context-free, context-sensitive, and recursively enumerable — fit neatly into a hierarchy called the Chomsky Hierarchy, shown below.
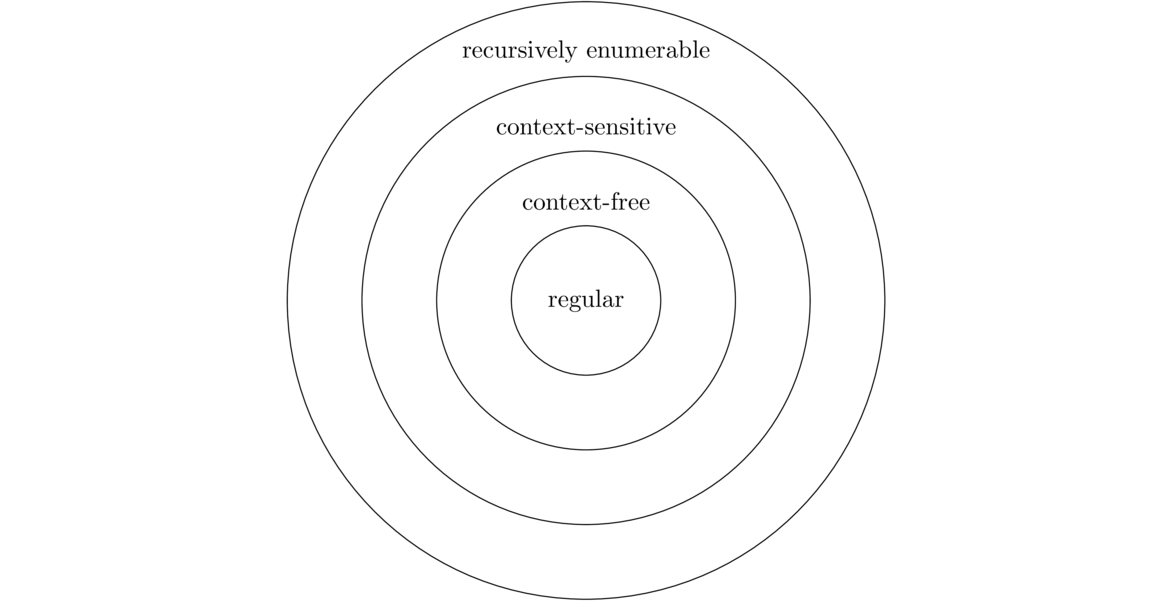
In particular, every regular language is a context-free language, every context-free language is a context-sensitive language, and every context-sensitive language is a recursively enumerable language. At each level of the hierarchy, there is a grammar type and an automaton type, as below:
| Level | Language Type | Grammar Type | Automaton Type |
| 0. | Recursively Enumerable | Unrestricted Grammar | Turing Machine |
| 1. | Context-sensitive | Context-sensitive Grammar | LBA |
| 2. | Context-free | Context-free Grammar | PDA |
| 3. | Regular | Right-linear Grammar | DFA |
Some of these levels can be broken into further levels. For instance, Level 0 can be broken into languages that are recursive and ones that are not. Level 2 can be broken into languages accepted by deterministic PDAs and ones that are not.
We will now show that some problems are undecidable (not recursive). That is, there are some languages for which we cannot build a Turing Machine that can tell us for sure, yes or no, whether a given string is in the language. To do this, we will use a little math.
Countability
A set is called countable if we can list its elements out and say that such and such is the first element, such and such is the second element, etc., with every element eventually appearing in the list. Formally, a set is countable if it is finite or we can find a one-to-one and onto function between it and the positive integers. Here are some examples:
- The set of all positive even integers is countable, because we can list its elements like below:
1. 2 2. 4 3. 6 4. 8 5. 10 … … Every even integer will eventually appear in this list.
- The set of all integers is countable. We can list its elements like below:
1. 0 2. -1 3. 1 4. -2 5. 2 6. -3 7. 3 … … Even though it seems like there are more integers than there are positive integers, in some sense there are the same amounts of both. This might seem a little weird, and it should, because infinity is a little weird.
- The set of all pairs (x,y) with x and y positive integers is countable. We can visualize the set as below:
1,1 1,2 1,3 1,4 … 2,1 2,2 2,3 2,4 … 3,1 3,2 3,3 3,4 … 4,1 4,2 4,3 4,4 … ⋮ ⋮ ⋮ ⋮ ⋱ It seems like there are truly a lot more pairs than there are positive integers, infinitely many more, but we can still list them out. The figure below suggests an approach where we sweep outwards from the upper left:
1,1 1,2 1,3 1,4 2,1 2,2 2,3 2,4 3,1 3,2 3,3 3,4 4,1 4,2 4,3 4,4 1,1 1,2 1,3 1,4 2,1 2,2 2,3 2,4 3,1 3,2 3,3 3,4 4,1 4,2 4,3 4,4 1,1 1,2 1,3 1,4 2,1 2,2 2,3 2,4 3,1 3,2 3,3 3,4 4,1 4,2 4,3 4,4 1,1 1,2 1,3 1,4 2,1 2,2 2,3 2,4 3,1 3,2 3,3 3,4 4,1 4,2 4,3 4,4 The list starts like this:
1. (1,1) 2. (1,2) 3. (2,2) 4. (2,1) 5. (1,3) 6. (2,3) 7. (3,3) 8. (3,2) 9. (3,1) 10. (1,4) … We start with (1,1). Then we list all the pairs whose highest entry is 2, then all the pairs whose highest entry is 3, etc. Any given pair will eventually appear somewhere in the list.
A similar argument can be used to show that the set of all rational numbers (fractions) is countable. A fraction like 3/5 can be identified with the pair (3,5), so if pairs are countable then so are (positive) rational numbers. We could then use an alternating trick like we used earlier to handle negatives.
- The set of all strings of 0s and 1s is countable.
Recall that strings are finite by definition. We can use a similar technique to the one just used — list the empty string, followed by all the strings of length 1, then all the strings of length 2, etc.
1. λ 2. 0 3. 1 4. 00 5. 01 6. 10 7. 11 8. 000 … … An uncountable set
Countability is a measure of how “big” an infinite set is. Some sets are too big to be countable. One such set is the set of all sequences of 0s and 1s. Unlike strings, sequences can be infinite in length. For instance, we can have the sequence (1,1,1,1,…) consisting of infinitely many 1s or the sequence (1,0,1,0,…) that alternates 10 forever.
To show this is not countable, let's pretend that it were actually possible to list the items out. We will arrive at a contradiction. Here is the first portion of one hypothetical list of all sequences:
1. 0 1 0 1 0 1… 2. 0 0 0 1 0 1 … 3. 1 1 1 1 0 1 … 4. 1 1 0 1 0 1 … 5. 0 0 0 0 0 1 … 6. 1 0 1 0 1 0 … … … Let's use this list to construct a new sequence. Take the first digit from the first sequence, the second digit from the second sequence, the third digit from the third sequence, etc. The first six digits are 0, 0, 1, 1, 0, 0. These come from the diagonal entries in the list, highlighted above.
Now take each of these and flip the 0s to 1s and the 1s to 0s:
Diagonal sequence: 001100… Flipped sequence: 110011… The flipped sequence is guaranteed to never appear in the list. Why? Each sequence in the list contributes to the constructed sequence; when we flip the digits, we are guaranteed that the flipped sequence disagrees with the first sequence in position 1, it disagrees with the second sequence in position 2, etc.
In short, given any supposed list of all the sequences of 0s and 1s, we can always use it to find a new sequence that is not anywhere in the list. Thus all sequences of 0s and 1s cannot be listed out, or counted. They are uncountable.
The process used above is referred to as diagonalization. A similar diagonalization argument can be used to show that the real numbers are uncountable. In fact, sequences of 0s and 1s can be thought of as just the binary expansions of real numbers.
Uncountable sets are just so much larger than countable sets. To picture the difference between the integers and the real numbers, think of the real numbers as an ocean and the integers as random pieces of driftwood floating on that ocean. Almost every number in some sense is not an integer.
How this applies to decidability
Recall that every Turing Machine can be represented as a string. As we saw above, the set of all strings of 0s and 1s is countable, so the set of all Turing Machines is countable as well (it's an infinite subset of the set of all strings of 0s and 1s).
And as we showed above, the set of all sequences of 0s and 1s is uncountable. Recall that languages over Σ = {0,1} are defined as sets of strings. Since the set of strings over Σ = {0,1} is countable, we can list all strings out, giving them names s1, s2, s3, etc. A typical language will have some of these strings but not others. We can associate each language with the sequence (x1, x2, x3. …), where xi is 1 if si is in the language and 0 otherwise. For instance, L = {s2,s4,s6,s8,…} is a language whose corresponding sequence is (0, 1, 0, 1, 0, 1, 0, 1, …). So languages are in one-to-one correspondence with sequences of 0s and 1s, and hence are uncountable.
So Turing Machines are countable and languages are uncountable. Thus there are some languages for which there is no Turing Machine to decide them. Hence some—in fact most—problems are undecidable. That is, of all the things out there that we might want to compute with a Turing Machine or an ordinary computer, most of them cannot be computed. On the other hand, most ordinary things that we might want to compute, like primes or Fibonacci numbers, are easy to compute. What do these uncomputable (undecidable) problems look like?
Undecidable Problems
In the last section, we saw that some problems are undecidable. Now let's look at some specific problems that we can show are undecidable.
Logical puzzles
The way we prove certain problems are undecidable is a little hard to grasp at first, but it is similar to some famous old logical puzzles. Here are a few:
- Can God create a stone so heavy that even he can't lift it? This puzzle dates back at least to medieval times. Here we assume that God is all-powerful.
The paradox is this: If God is all powerful, then of course he could create such a stone, but then by definition, he couldn't lift the stone, which contradicts that he is all powerful.
This paradox is called the Omnipotence paradox. Wikipedia has an interesting page about it.
- In a logic class, your whole grade is based on a single statement you have to make. If you make a true statement, then you get a course grade of 20% and you fail the course. If you make a false statement, then you get a grade of 10% and you fail the course. Is there any hope?
The trick is to make the following statement: “I am going to get a grade of 10% in the course.” This can't be a true statement, because if it were true, then you would get 20% in the course. But it also can't be a false statement, because if it were false, then you would get 10% in the class, which would make the statement true.
The statement is neither true nor false, so the professor would have no choice but to conclude you know some logic and let you pass the course.
- The Barber of Seville — The Barber of Seville shaves all men, and only those men, who don't shave themselves. Who shaves the barber?
This is a paradox invented in the early part of the 20th century to demonstrate some logical problems that were plaguing the foundations of mathematics at that time. To work with it, you need to make some assumptions, like that the barber is a male and that Seville is the only town around.
The paradox comes in when we think about who shaves the barber: If he shaves himself, that breaks the rules because he only shaves men who don't shave themselves. But no one else can shave him because then he wouldn't shave himself, and he shaves everyone who doesn't shave himself.
All three of these paradoxes have a few things in common. First, they involve trying to give someone too much power. Second, they involve some sort of feedback mechanism. In the first example God tries to do something even he can't do. In the second example, the statement the student makes uses the rules of the grading system. In the third example, we feed the barber into the barber function, so to speak.
These themes will now come up when we try to show that some problems are undecidable.
The problem of determining if a Turing Machine accepts a string
Here is the problem: create a Turing Machine H that takes as input a Turing Machine M and a string w and returns a definite yes/no answer as to whether M accepts w. This is the Turing Machine Acceptance Problem.
We will think of this Turing Machine H as a function H(M,w) that takes a Turing Machine M and a string w and returns “accept” or “reject”. For simplicity's sake, we will talk about inputting a Turing Machine M into H, but what we really mean is that we are inputting a string representation of M.
Here is how we show the problem is undecidable: Assume that such a Turing Machine H exists. Create another Turing Machine D based on H. Its input is a Turing Machine M. Then D runs H(M,M), but with a twist: if H accepts, then D will reject, and it H rejects, then D will accept. Now look what happens when we try to do D(D) (feeding D into itself):
- If D accepts itself, then H(D,D) must output “reject”, which by the definition of H means that D rejects itself.
- If D rejects itself, then H(D,D) must output “accept”, which by the definition of H means that D accepts itself.
Either way, we get a contradiction. The machine H therefore cannot exist.
A diagonalization version of the proofPeople sometimes do this proof with a diagonalization argument. We make a table where the rows are all the Turing Machines. There are a countable number of Turing Machines, so it is possible to list them out as the rows of the table.
The columns are the Turing Machines in the same order. The table entry in row r, column c is “accept” or “reject” based on whether or not the Turing Machine in row r accepts the Turing Machine in column c. The table entries are thus the outputs of H(Mr, Mc). Here is a hypothetical version of this table, where A = accept and R = reject):
M1 M2 M3 M4 M5 M6 … M1 R R A A R R … M2 R R R A A A … M3 A A A R A R … M4 A R R A R A … M5 R A R R R R … M6 A A R A A R … ⋮ ⋮ ⋱ We then create the Turing Machine D by running down the diagonal, taking the outputs there, and flipping them. In particular, D's outputs on M1 through M6 in the hypothetical example above would be A, A, R, R, A, A.
Every Turing Machine appears in this table somewhere, so D must appear. Now look at the output of D(D). This is the diagonal entry in the table in the row and column that D appears in. We get a contradiction because D is defined by flipping everything on the diagonal. If the table entry at that diagonal for D's row and column is an A, then by the definition of D, we must have D(D) = R, which is impossible because D(D) = A by the table definition. A similar problem happens if the diagonal entry is an R.
Thus we have a contradiction, which means that it is impossible to build such a table. The table entries are given by the Turing Machine H, so H can't exist.
The Halting Problem
More famous than the Turing Machine Acceptance Problem is the Halting Problem. It asks the following: given a Turing Machine M and an input string w, does M halt on w? That is, can we say for sure that M stops and doesn't get caught in an infinite loop?
Put another way, is it possible to create a Java program that takes Java programs as inputs and tells us for sure whether or not those programs will eventually stop running?
This is another undecidable problem. We can use the Acceptance Problem to show this. In particular, we show that if we can decide the Halting Problem, then we use that to decide the Acceptance Problem, which we know is impossible.
Here is how the proof goes: Suppose H is a Turing Machine that decides the Halting Problem. Now suppose that we have a Turing Machine M and a string w and we want to know if M accepts w or not (this is the Acceptance Problem). Run H(M,w) to see if M halts on w. If H tells us that M does not halt on w, then we know that M will not accept w. If H tells us that M does halt on w, then run M on w and see whether it accepts or rejects. Since M halts in this case, we are guaranteed to get an answer. In every case, we get a definite yes or no answer as to whether M accepts or rejects w. But this is impossible, so a Turing Machine that decides the Halting Problem cannot exist.
The idea of this proof is that a Turing Machine that decides the Halting problem is a very powerful machine indeed. It is so powerful, it can do things that can't be done, like help us decide the Acceptance Problem.
More undecidable problems and Rice's Theorem
Consider the problem of deciding if a Turing Machine accepts any strings at all. This problem is undecidable. To see why, suppose there exists a Turing Machine that takes Turing Machines as inputs and tells us if they accept any strings at all. We will call this machine an “empty checker”, and we will use it to decide the Acceptance Problem.
Suppose we are given a Turing Machine M and a string w, and we want to know if M accepts w or not. We create a new Turing Machine H that takes an input string x and compares it to w. If x ≠ w, then H automatically rejects x. If x = w, then we run x on M, and H accepts if M accepts. The key feature of this Turing Machine is that it rejects everything except possibly for w.
Now take H and use it as input to the empty-checker. If the empty-checker tells us that H accepts nothing at all, then we know that it must reject w, since w is the only string H can possibly accept. Hence M rejects w. Likewise, if the empty-checker tells us that H does accept some strings, then we know H accepts something, and that something can only be w. And by the definition of H, M must accept w. In either case, we have decided the Acceptance Problem, which is impossible, so the empty-checker cannot exist.
This proof relies on cleverly constructing a machine that we could use in conjunction with the empty-checker to decide an undecidable problem. This and the previous proof are examples of reduction proofs, which are important in computer science. The idea of a reduction proof is reducing problem A to problem B, i.e., showing that you can use A to solve B. If B is impossible to solve, then so is A.
The same technique used here can be extended to prove a more general theorem, called Rice's Theorem. It says the following:
Rice's Theorem: Any nontrivial property of Turing Machines is undecidable.
By “nontrivial”, we mean that it is a property that is not true of all Turing Machines. Trivial properties would be deciding if a Turing Machine accepts at least 0 strings, or deciding if it has a finite number of states.
But anything nontrivial will be undecidable, like deciding if a given Turing Machine accepts all strings, or infinitely many strings, or if it accepts the empty string, or if there is some input on which it loops forever, or if it needs to overwrite any cells on its input tape. Note that for any single Turing Machine we can often answer these questions; Rice's Theorem says that we can't come up with something that will answer these questions for every possible Turing Machine.
By contrast, almost any question about regular languages is decidable. Regular languages and DFAs are simple enough that most questions we might ask about them can be answered. Turing Machines are just too powerful and varied for us to ever have nontrivial blanket statements that cover all of the possibilities. For instance, the way some people explain why the Halting Problem is undecidable is that there are infinitely many different kinds of infinite loops, with no way to possibly check for all kinds.
For the languages in the middle of the Chomsky Hierarchy—context-free and context-sensitive—some problems are decidable, though most interesting ones are not. For instance, the Acceptance Problem for context-free and context-sensitive languages is decidable. The problem of determining if a PDA accepts anything at all is decidable, but it is undecidable for LBAs. On the other hand, the problems of determining if a PDAs and LBAs accepts all strings in Σ* are undecidable.
The Post Correspondence Problem
Many of the undecidable problems we have seen are somewhat abstract. Here is a more practical problem that is undecidable. Suppose we are given two families of strings, like the ones shown below:
A B 1. 10 1 2. 010 01 3. 01 001 Consider a sequence like (3, 2, 1). We concatenate strings 3, 2, and 1 from family A to get 01+010+10 = 0101010. We do the same thing with B to get 001+01+1 = 001011. Are these equal? No.
We are interested in if there is a sequence that does produce equal strings. One example is (2, 3), which produces 01001 from both families.
Here is another set of two families:
A B 1. 0 1 2. 00 11 3. 000 111 It should be pretty clear that there is no sequence that could possibly produce equal strings from these two families.
The Post Correspondence Problem asks for an algorithm (or Turing Machine) that is given two families and tells us whether a sequence exists or not that produces equal strings from both families.
This seems like a totally reasonable thing to try to program, but it is impossible. The impossibility proof is a reduction proof to the Turing Machine Acceptance Problem, but the details get a little messy, so we will not include the proof here.
Note that the problem is at least recognizable (recursively enumerable). We could write a program that tries all possible sequences systematically, starting with sequences of length 1, then length 2, etc. If there is a solution, we will eventually find it. But if there is no solution, then this brute-force search will run forever, and any time we check on the search, we can never be sure if a solution is just around the corner or if the program is taking so long because there is no solution to be found.
Also note that though the problem is undecidable, it is still decidable in specific instances, as we saw in the examples above. The undecidable part is that we cannot build a single algorithm that will work for all possible families of strings.
Unrecognizable problems
The Post-Correspondence Problem, Acceptance Problem, and Halting Problem are all undecidable, but they are still recognizable. We can get partial “yes” answers for all of them, but not definite yes-or-no answers. Are there problems where not even partial answers are possible? Yes. Here is a short theorem:
Theorem: If a language L is recognizable and its complement L is recognizable, then L is decidable.
Here's why it is true: Since L and L are recognizable, there exists a Turing Machine M for L and a Turing Machine M' for L. Let's use these to build a decider for L: Given an input string w, run w on both M and M'. If w is in L, then eventually M will halt and accept w. If w is not in L, then eventually M' will halt and accept w. In either case, we get a definite yes/no answer as to whether w is in L.
A consequence of this theorem is if L is recognizable but not decidable, then L cannot be recognizable (as otherwise L would be decidable). So the complements of any of the problems we have shown to be undecidable are all unrecognizable.
For instance, determining if a Turing Machine eventually halts on a given input is undecidable but recognizable. The complement of this problem, determining if a Turing Machine loops forever on a given input, is undecidable and unrecognizable.
To determine if M halts on w, we can run M on a Universal Turing Machine and if it does halt, then eventually that UTM will halt, and we will get a yes answer. If it doesn't halt, then we can't be sure if it is stuck in an infinite loop or just taking a long time to halt. But to determine if M loops forever on w, we can't even get a definite yes answer. If we run M on a UTM, it won't ever stop and so we won't be able to get a yes answer.
Coda
Having come to the end of these notes, it's worth taking a moment to consider why it's worth learning this stuff. First, it's nice to have some answers to questions like these:
- What does it mean to compute things?
- What are the strengths and limitations of various models of computing?
- What can't be computed by any computing machine?
At a more practical level, becoming good at constructing DFAs can help with writing better programs. Thinking of a problem as consisting as a series of states with transitions between them can be very helpful. Grammars are particularly useful to understand because modern programming languages are usually defined by grammars.
To learn more about all of this, see any standard textbook on automata/formal languages/theory of computation. One particularly good one is Introduction to the Theory of Computation by Michael Sipser.
Exercises
Exercises for Chapter 1
- Let Σ = {a,b,c}. Consider the strings u = aaba and v = ccc. Find the following:
(a) uv (b) v3 (c) uR (d) |u| - Let Σ = {a,b,c}. Consider the languages M = {b, cc} and N = {abc, cc, cba}
- Find M ∪ N and M ∩ N.
- List all the elements of length 4 in M*.
- List all the elements of length 1 in M.
- List all the elements of MN.
- Given the alphabet Σ = {a,b} and the language {anb2n+1 : n ≥ 0}, list five different strings in the language.
Exercises for Chapter 2
- Answer the questions about the DFA below on the left.
- Give the sequence of states that the input string 000101 passes through.
- Give a clear description of the language accepted by the DFA.
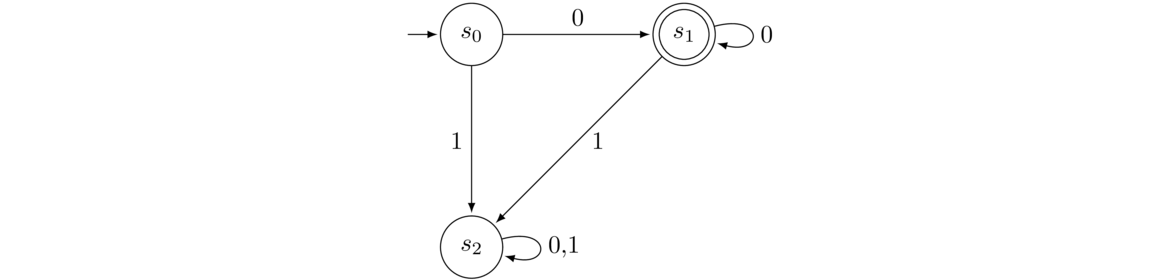
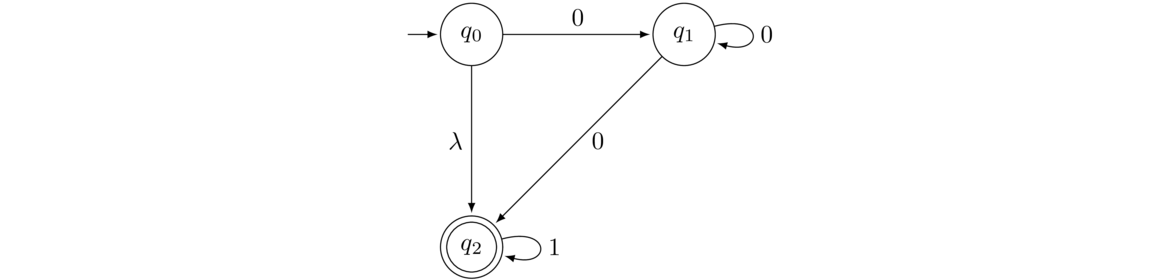
- Answer the questions about the NFA above on the right.
- Give two distinct paths that the input string 000 can take through the NFA.
- Give a clear description of the language accepted by the NFA.
- Indicate which states and transitions specifically make this automaton nondeterministic.
- Construct DFAs that accept the following. Assume Σ = {0,1}.
- All strings of length at most 1
- All strings that start with 1
- All strings that end with 01
- ∅ (i.e., the DFA accepts nothing at all)
- All strings of length 3 or less
- All strings with an odd number of ones
- Only these strings: {0, 01, 11, 101}
- All strings that have at most two 0s and at most three 1s
- All strings of the form 0*10* that consist of some number of 0s followed by a 1 followed by some number of 0s (in both cases, there could be no 0s)
- All strings that have at least two 0s and end with 1
- All strings that start with 1 and end with 0
- All strings that end with a different symbol than they start with
- All strings that start with 0 and have odd length or start with 1 and have even length
- Create NFAs for the following. Assume Σ = {0,1}. Make sure your NFA has exactly the number of states required.
- All strings that start with 11 (3 states)
- All strings ending with 111 (4 states)
- All strings containing the substring 010 (4 states)
- Only the string 1 and nothing else (2 states)
- All strings of the form 0*1*0* (3 states). This is all strings that consist of any number of 0s followed by any number of 1s, followed by any number of 0s, where “any number” includes the possibility of none at all.
- Describe how to turn any NFA with multiple accepting states into a new NFA that has only one accepting state. The new NFA should accept precisely the same strings as the old one.
- Convert the following NFAs to DFAs using the powerset construction. Label each state with subsets, as described in the notes.
- The NFA given in Problem 2
- The NFA below on the left

- The NFA above on the right
- Consider the automata from problems 1 and 2. Let L and M be the languages accepted by each of these. Construct NFAs that accept the following languages:
- LM
- L*
- L ∪ M
- L
- LR
- The first DFA below accepts a certain language L. Below it are two potential ways to create an NFA that accepts L*. Only one of them is correct. The other accepts some strings that are not in L*. For the incorrect NFA, give an example string that it accepts that is not in L*.
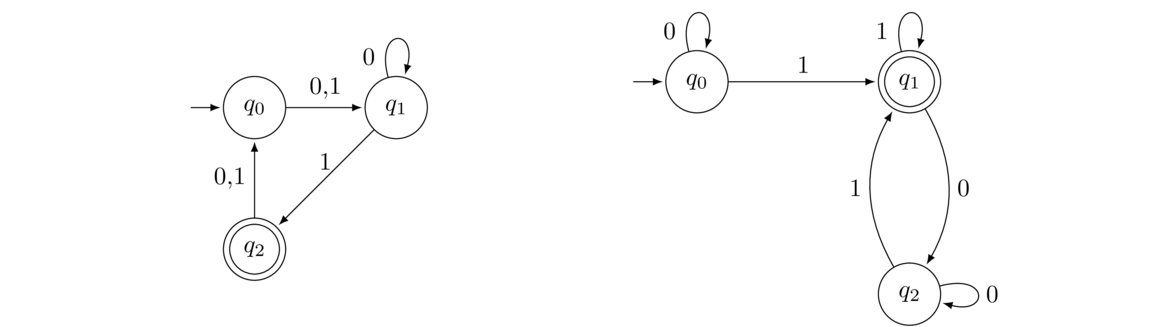
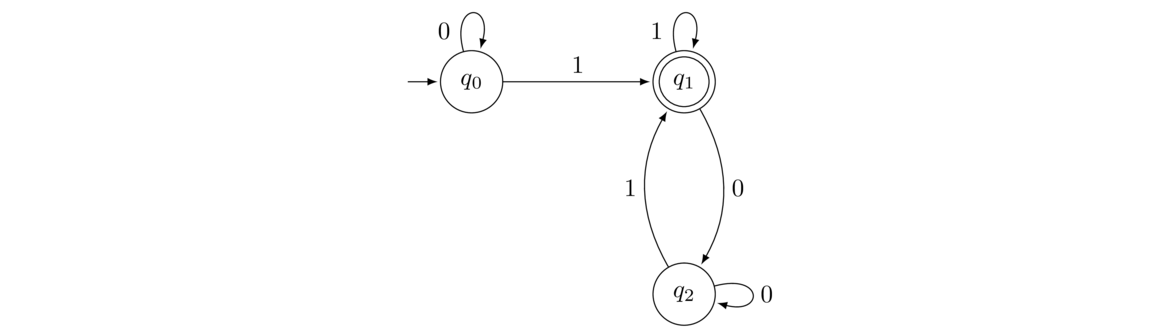

Exercises for Chapter 3
- Consider the regular expression 0*(λ + 1) + (0+1)(0+1). Describe in English the language that this expression generates.
- List all the different strings of length 6 that are described by the regular expression 11(11+00)*.
- List all the strings of length at most 5 that are described by the regular expression (λ+0)1(01)*.
- Find regular expressions for the following. Assume the alphabet is Σ = {0,1} unless specified otherwise.
- All strings that consist of any amount of 0s followed by at least one 1
- All strings of length 3
- All strings containing the substring 10110
- The strings 00, 010, along with anything that starts with a 1
- All strings except those that contain exactly 2 symbols
- Using Σ = {0}, all strings of 0s where the number of zeroes is congruent to 1 mod 3 (i.e., leaves a remainder of 1 when divided by 3)
- All strings in which every 1 is followed by at least two 0s
- All strings that contain a substring that consists of a 1 followed by at least one 0 followed by another 1
- All strings that start with 0 and end with 1
- All strings that start and end with different symbols
- All strings except 00 and 11
- Convert the following regular expressions into NFAs.
- 0*1+1*0
- (11+0)*+0*1
- Convert the DFAs below to regexes.

- Suppose we are trying to use the Pumping Lemma to show the language of all even-length palindromes in not regular. Explain what is wrong with each of the following attempts.
- Given n from the opponent, choose the string s = 0110. [Rest of proof omitted because the problem is with s.]
- Given n from the opponent, choose the string s = 0n1n. [Rest of proof omitted because the problem is with s.]
- Given n from the opponent, choose the string s = 02n. Then assuming the opponent breaks the string into xyz according to the rules of the pumping lemma, xy2z is not in the language because it has too many 0s.
- Given n from the opponent, choose the string s = 0(0110)n0. Then break the string into xyz such that x is empty, y is the first 0, and z is the rest of the string. Then xy2z will have an odd length, so it won't be in the language.
- Suppose Σ = {0,1} and L is the language of all strings with more 0s than 1s. We are trying to prove this language is not regular using the Pumping Lemma. But every attempt to use it is wrong. Explain precisely what the most important mistake in each attempt is.
- Let n be given. Consider the string 1n0n. No matter how it is broken up into x, y, and z according to the rules of the pumping lemma, we have x and y consisting of all 1s. Then xy2z has more 1s than 0s, a contradiction.
- Let n be given. Consider the string 010n. If we break it up into x = 0, y = 1, and z = 0n, then xyn+2z has more 1s than 0s, a contradiction.
- Let n be given. Consider the string 11000. No matter how it is broken up into x, y, and z according to the rules of the pumping lemma, we have x and y consisting of all 1s. Then xy4z has more 1s than 0s, a contradiction.
- Suppose we try to use the Pumping Lemma to show that the language given by the regular expression 0*1* is not regular. Suppose the opponent chooses n and we choose the string 0n1n. Show that the opponent has a way to break our string into xyz such that xykz is always in the language.
- Use the Pumping Lemma to show that the following languages are not regular. Assume Σ = {0,1} unless otherwise noted.
- The language of all even-length palindromes.
- The language of all words of the form ww, where a word is followed by itself. Examples include 0101 (w = 01) and 110110 (w = 110).
- The language {0i1j0k : k = i+j}.
- The language of all strings that contain more 0s than 1s.
- Using Σ = {0}, the language of all words of the form 0m where m is a power of 2. [Hint: use the fact that j<2j for any positive integer j. Also, |xy2z| = |xyz|+|y|.]
- The language {0n1m : n ≠ m}. [Hint: this is the trickiest problem. Factorials are helpful here.]
- Let Σ = {0,1}. Consider language {0n1m : n ≥ 100, m ≤ 100}. Prove that it is regular. [Hint: What is the definition of a regular language?]
Exercises for Chapter 4
- Consider the grammar below.
A → BC | D
B → bbB | λ
C → aCb | a
D → aD | λ
- Give a parse tree for the string bbbbaab.
- Give a leftmost derivation for the string above.
- Give another derivation that is not a leftmost derivation for the same string.
- Consider the grammar below.
S → A | bSb
A → aA | a
- Give a parse tree for the string bbaabb.
- Give a derivation for the same string.
- Consider the grammar below.
A → AB | Ab | λ
B → aB | Bb | λ
- Give a parse tree for the string aba.
- Give a derivation for the string bb.
- This grammar is ambiguous. Give a particular example to illustrate why.
- Give clear descriptions of the languages generated by the following grammars.
- The grammar given by S → aSb | bSa | λ doesn't generate all strings of equal numbers of a's and b's.
- Give an example string with equal numbers of a's and b's that is not in the language generated by the grammar.
- What is it about the grammar that causes it to miss the string you gave as an answer to part (a)? Try to give a reason that is enlightening.
- Suppose we want to create a context free grammar for all strings of the form ambmcn, where m and n can be any integers greater than or equal to 0. We come up with the following:
S → aSbC | λ
C → cC | λ
Give an example of a string that is in the language generated by this grammar that is not of the form ambmcn along with a parse tree or derivation showing the string is in the grammar.
- Suppose we are trying to create a grammar for all strings of the form anbnc with n ≥ 0. We come up with S → aSbc | λ. Give an example of a string that is in the language generated by this grammar that is not of the desired form.
- Construct context-free grammars for the following. Assume Σ = {a,b} unless noted otherwise.
- All strings of the form ambn with m ≥ 2 and n ≥ 1
- All strings that start and end with the same letter
- All strings of just a's where the number of a's is a multiple of 3
- All strings of just a's where the number of a's is not a multiple of 3
- All strings that have an odd length and whose middle symbol is an a
- All strings that are odd length palindromes
- All strings of the form anbn+1 with n ≥ 0
- All strings of the form anbnakbk with n,k ≥ 0
- All strings of the form anbnakbk with n,k ≥ 2
- All strings of the form anbn a2mb2m where m,n ≥ 0
- All strings of the form anbm or of the form (ab)k with m,n ≥ 0 and k ≥ 2
- All strings of the form anbn or anb2n with n ≥ 0
- All strings of the form anbn where n is odd
- All strings of the form anbmck, where m = n or m = k
- All strings of the form anbm with n ≤ m+3
- Convert the DFA below to a right linear grammar.
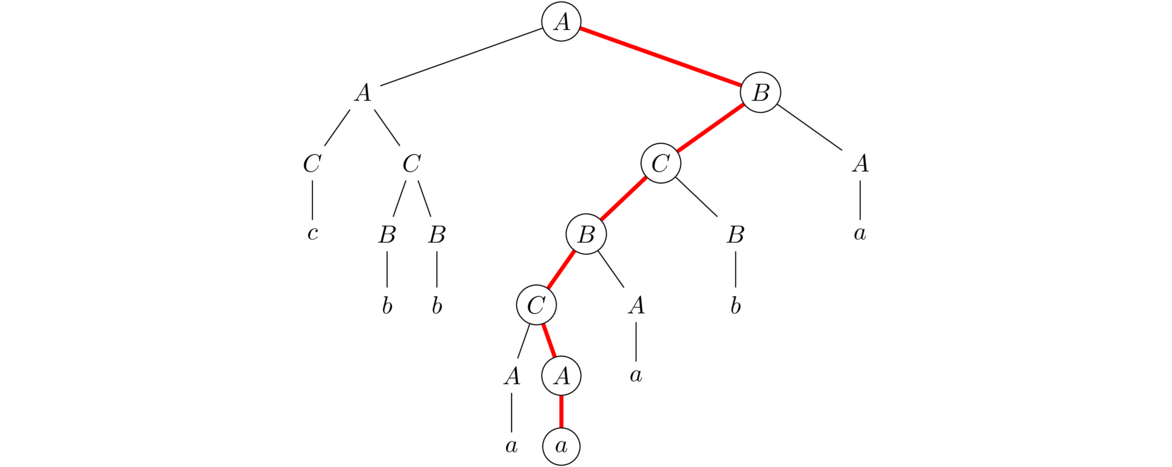
- Convert the right linear grammar below to an NFA.
A → B | 0C
B → 1 | 010C
C → 0C | 1 | λ
- The grammar below has λ productions and unit productions. Remove them according the process used in finding Chomsky normal form.
A → aBCBb | C
B → ab | CCb | λ
C → bB | a
- Convert the following grammar to Chomsky Normal Form (note there are no λ or unit productions).
A → BCC | aaC
B → BCCB | b
C → aaba | ba
- The grammar below has λ productions and unit productions. Remove them according the process used in finding Chomsky normal form.
A → aCaaCbC | B
B → ab | Cb
C → cC | λ
- Convert the following grammar to Chomsky Normal Form (note there are no λ or unit productions).
A → BCB | abC
B → BBCC | a
C → a | b
- Convert the grammar below to Chomsky Normal Form. Show every step in detail and remove any useless rules that arise at any point in the process.
S → AAB | AS | baB
A → aA | λ
B → ABaa | C
C → abb | aB
Exercises for Chapter 5
- Answer the questions about the PDA below.
The notation on the loop on q1 is a shorthand for four possible transitions: if the current input symbol is an a or a b and there is a 1 on top of the stack or the stack is empty, then stay at q1 and push a 1 onto the stack. For parts (a), (b), and (c), assume that the transition from q0 to q1 is always taken.
- Consider the input string abbbcccc. Give the sequence of states the input string will lead to. For each state in your sequence, please also list the full contents of the stack at that point.
- Repeat the previous part for the input string abcca.
- Repeat the previous part for the input string c.
- If we were to remove state q0 and make q1 the initial state, there is precisely one string that would be no longer be accepted by the PDA. What string is that?
- What is the language accepted by this PDA?
- Consider the PDA below.

- Consider the input string ab#ba. Give the sequence of states the input string will lead to. For each state in your sequence, please also list the full contents of the stack at that point.
- Consider the input string ab#ab. Give the sequence of states the input string will lead to. For each state in your sequence, please also list the full contents of the stack at that point.
- Is this PDA deterministic or not? How do you know?
- What is the language accepted by this PDA?
- Construct PDAs that accept the following languages.
- All strings of the form 0n+11n with n ≥ 0.
- All strings of the form 0n1k0n with n,k ≥ 1.
- All strings of the form 0n1k2n with n,k ≥ 1.
- All strings of the form 0n1k2k3n, with k,n ≥ 1.
- All strings of the form 0k1n with k < n and k, n ≥ 1.
- All strings of properly balanced parentheses. Parentheses are balanced if every opening parenthesis has a corresponding closing parenthesis, and the parentheses are properly nested. Assume the parentheses are “(” and “)”.
- Convert the following grammars to PDAs.
-
A → BC | b
B → BB | AC
C → a | c
-
A → BA | CC
B → AB | b
C → a | b
-
- Shown below is a parse tree for the string cbbaaaba in a particular grammar. A particular path in the parse tree has been highlighted. Starting from the bottom of the path, the first repeated variable is C.
- Give the breakdown of the string into vwxyz that is caused by this path (just like is done in the notes).
- Sketch a new parse tree showing how this string is pumped up to vw2xy2z by replacing a certain part of the parse tree with something else (just like is done in the notes).

- Consider the language of all strings of 0s and 1s where the number of 0s equals the number of 1s. This language is context-free. If we try to use the CFG pumping lemma on this language, something should go wrong. In particular, suppose the opponent chooses n and we choose the string 0n1n. Show that there is a breakdown into vwxyz that the opponent can choose such that vwkxykz is still in the language for all k ≥ 0.
- Consider the language of all 0s and 1s with equal numbers of both. We are trying to use the Context-free Pumping Lemma to show the language is not context free. Given n, we choose s = (01)n. Show that there is a breakdown into vwxyz that the opponent can use such that vwkxykz is always in the language for any k ≥ 0.
- Suppose we try to use the Context-free Pumping Lemma to show that the language of strings of the form w#w is not context-free. Given n, we use the string 0n1n#0n1n. We then consider breakdowns into vwxyz according to the rules. Briefly describe the different cases we would need to consider to finish the proof.
- Consider the language of all strings of 0s, 1s, and 2s, where the number of 0s, 1s, and 2s are all equal. Use the Context-free Pumping Lemma to show that this is not a context-free language.
Exercises for Chapter 6
-
For each problem below, build a Turing Machine for it. Answer it in two parts:
(a) Give an English description of the strategy used.
(b) Give a state diagram of the Turing machine.
You may want to use the online simulator at https://turingmachinesimulator.com/ to test your work. For any of these, you can assume there is a blank before the first symbol of the input if you want. Part (a) is done for you so you can see what your answers should look like.
- A TM for the language of strings of the form 0n1n.
Answer:
- Start by overwriting the first 0 with a blank. Then move all the way to the end of the string and overwrite the last 1 with a blank. Then move back to the front of the string and repeat the whole process. Keep doing this until there are only blank symbols left.
-

- All strings of the form (0+1)1*
- All strings of 0s and 1s with an odd number of 0s.
- All strings of 0s and 1s with an equal number of 0s and 1s.
- All strings of 0s and 1s of the form w#w, where the same string of 0s and 1s is repeated with a # character in between. Examples include 01#01 and 1101#1101.
- A TM that takes a string of all 0s and doubles it. For instance, if the tape initially contains 000, then when the TM is done, the machine would contain 000000. It should go to an accepting state when it has finished, and the read head should be positioned on the blank right after the last 0. You can assume there are no 1s in the input string.
- A TM for the language of strings of the form 0n1n.
- In our initial definition of a Turing Machine, it had a fixed left end, but the right side extended to infinity. Later, we looked a Turing Machine with a tape that was infinite in both directions, and built an ordinary Turing Machine from it. Suppose the bi-infinite version has the following symbols in tape indices -2 to 5:
0 1 1 X 0 X 0 0. All other symbols are blank. Sketch the tape contents of the ordinary Turing Machine we construct from this (doing the same construction we did in the notes). - Suppose we have a 3-tape Turing Machine with the following tape contents:
Tape 1: 101101
Tape 2: 001
Tape 3: 01001
The rest of each tape is blank. The underlined items correspond to the locations of the read heads.
- Sketch what the single-tape version of this looks like, according to the process given in the notes.
- Describe the process that the single-tape TM will take given the transition
1,X,L | 0,0,R | 0,Y,R. In particular, describe exactly where the read head of the single-tape TM will move and what the tape will look like after the process has finished dealing with the transition.
- Fill in the blanks.
One key difference between DFAs and Turing Machines is that while both DFAs and Turing Machines can accept or reject an input string, it is possible for a Turing Machine to also . Another key difference is that when a DFA reaches an accepting state, the machine may keep going, while when a Turing Machine reaches an accepting state, .
- When showing that nondeterministic Turing Machines are equivalent to deterministic ones, we used a breadth-first search, not a depth-first search. Why would DFS not work?
- The Church-Turing thesis is called a “thesis” because we can't actually verify that it is true. What is it about the statement that makes it impossible to verify?
- When talking about undecidability, we often feed a Turing Machine as input into another Turing Machine. But the inputs of Turing Machines are only supposed to be strings. How then can a Turing Machine be an input to another Turing Machine?
- What is the name of the type of automaton that corresponds to a Turing Machine whose tape length is fixed at the size of the input string?
- What is a Universal Turing Machine?
- For the Universal Turing Machine given in the notes, describe exactly what each of its three tapes is used for.
- Choose the best answer.
- A DFA with two unbounded stacks to use as memory is (less powerful than / as powerful as / more powerful than) an ordinary Turing Machine.
- A DFA with a 10-item list to use as memory is (less powerful than / as powerful as / more powerful than) an ordinary Turing Machine.
- A Turing Machine whose tape alphabet consists of the blank symbol and the symbols 0 and 1 is (less powerful than / as powerful as / more powerful than) an ordinary Turing Machine.
- A Turing Machine that is able to perform infinitely many computational steps in each transition is (less powerful than / as powerful as / more powerful than) an ordinary Turing Machine.
- A DFA with a queue to use as memory is (less powerful than / as powerful as / more powerful than) an ordinary Turing Machine.
- A Turing Machine whose tape length is not infinite is (less powerful than / as powerful as / more powerful than) an ordinary Turing Machine.
- True or false:
- Given any regular language, there is a Turing Machine that accepts precisely that language.
- Every context-free language is also a context-sensitive language.
- Every Turing Machine can be encoded as a finite string of 0s and 1s.
- There is a Turing Machine that is able to simulate any other Turing Machine.
- Give a derivation of the string aabb in the grammar below:
S → SAB | λ
AB → BA
BA → AB
A → a
B → b
- Give a derivation of the string aabcc in the grammar below:
S → aSb | λ
Sb → C
C → cC | λ
Cb → bC
- Give an example of a Turing Machine that enters into an infinite loop on the input string
0but not on any other strings. - Suppose we create a modified Turing machine that on any transition can write to the tape or move the read head, but it can't do both at once. Explain why it is equivalent to an ordinary Turing machine.
- Consider a modified Turing Machine that allows us to move the read head by multiple cells in a single transition. For instance, we might have a transition like 0,0,RRR that says that if we read a 0, then we write a 0 and move the read head three cells right. Show that this modified Turing Machine is no more powerful than an ordinary Turing Machine.
Exercises for Chapter 7
- True or false:
- If a language is recursive, then it is also recursively enumerable.
- If a language and its complement are both recursively enumerable, then the language is itself recursive.
- While some languages are not decidable (recursive), every language is at least recognizable (recursively enumerable).
- Choose the best answer:
(a) All languages are decidable by Turing Machines.
(b) Most languages are decidable by Turing Machines.
(c) Most languages are not decidable by Turing Machines. - Which of these are decidable (recursive)?
- Given a Turing Machine M and an input string w, determining whether M accepts w
- Given a Turing Machine M and an input string w and determining whether or not M gets caught in an infinite loop on w
- Determining if a DFA accepts all strings of 0s and 1s.
- Given a 3-tape Turing Machine for a language, determining if there is a 1-tape Turing Machine that accepts the same language
- Given a Turing Machine, determining if it accepts the same strings as another Turing Machine.
- Given a DFA, determining if it accepts the empty string.
- Given a context-free grammar, determining if it generates every string in Σ*.
- Consider the Post Correspondence Problem with the string families shown below.
A B 1. 101 01 2. 11 110 3. 01 11 - Find a solution to it.
- Why does your answer to part (a) not contradict the fact that the PCP is an undecidable problem?
- Show that the set of all even integers (positives and negatives and 0 included) is countable.
- There are a countable number of Turing Machines and an uncountable number of languages. What is the consequence of these two facts, taken together?
- In the diagonalization proof that the set of all sequences of 0s and 1s is uncountable, suppose we have listed out the following 6 sequences as the first 6 in a supposed list of all the sequences:
010101…
111111…
000000…
100100…
101010…
011011…
The diagonalization proof says to use this sequence to create a sequence that is not in the list. What are the first 6 numbers in such a sequence, according to the process described in the notes?
- Recall that we showed that there is no Turing Machine that can take a Turing Machine M and string w as input and give a definite yes/no answer as to whether M accepts w. But Universal Turing Machines simulate other Turing machines. Explain why a Universal Turing Machine would not work to tell us if M accepts w.
- Explain the Barber Paradox and how it relates to proving that there is no Turing Machine that can take a Turing Machine M and string w as input and give a definite yes/no answer as to whether M accepts w.
- Is it possible to write an algorithm that can tell whether any given Turing Machine is stuck in an infinite loop or if it will eventually reject a given string?
- In order to show a problem is undecidable, we start by assuming that there exists a Turing Machine that decides the problem. We use that machine to do what?
- We did a reduction proof to show that the problem of determining whether a Turing Machine accepts any strings at all is undecidable. The key idea was to construct a new machine and use it do something impossible. Explain in your own words how that all works.
- Show that the problem of determining if a Turing Machine accepts the empty string is recursively enumerable.
- Is the problem of determining if a Turing Machine accepts all strings recursively enumerable? Explain.
Bibliography
Here are the most useful references I found when preparing these notes.
- Lectures on YouTube by Shai Simonson (a compilation of them is here: http://coderisland.com/theory-of-computation-materials/). This was probably the most useful resource for me. He explains things very clearly.
- Introduction to the Theory of Computation, 3rd edition by Michael Sipser, Cengage, 2012 — This is a widely used textbook. It's concise and contains a large number of exercises. It's a very nice book overall.
- Introduction to Computer Theory, 2nd ed. by Daniel Cohen, Wiley, 1996 — Cohen's book is in some ways the opposite of Sipser's. Where Sipser is concise, Cohen is expansive. This is helpful when Sipser's explanations aren't detailed enough, but it can be hard to wade through all of Cohen's text on other topics to get the main idea.
- Formal Language — A Practical Introduction by Adam Brooks Webber, Franklin, Beedle & Associates, Inc., 2008 — This book has some nice explanations of things, along with some helpful examples and material on practical applications.
In addition, I occasionally referred to Wikipedia, An Introduction to Formal Languages and Automata by Linz, Foundations of Computation by Critchlow and Eck, Introduction to Theory of Computation by Maheshwari and Smid, and the notes here: https://courses.engr.illinois.edu/cs373/sp2009/lectures/.
- The set of all strings of 0s and 1s is countable.