A Practical Introduction to Python Programming
© 2015 Brian Heinold
Licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 Unported License
Here is a pdf version of the book.
I don't have solutions available to the exercises here, but here is a separate set of a few hundred exercises and solutions.
Here is a quick reference guide.
Text files needed for Chapter 12 and some exercises are available here.
My goal here is for something that is partly a tutorial and partly a reference book. I like how tutorials get you up and running quickly, but they can often be a little wordy and disorganized. Reference books contain a lot of good information, but they are often too terse, and they don't often give you a sense of what is important. My aim here is for something in the spirit of a tutorial but still useful as a reference. I summarize information in tables and give a lot of short example programs. I also like to jump right into things and fill in background information as I go, rather than covering the background material first.
This book started out as about 30 pages of notes for students in my introductory programming class at Mount St. Mary's University. Most of these students have no prior programming experience, and that has affected my approach. I leave out a lot of technical details and sometimes I oversimplify things. Some of these details are filled in later in the book, though other details are never filled in. But this book is not designed to cover everything, and I recommend reading other books and the Python documentation to fill in the gaps.
The style of programming in this book is geared towards the kinds of programming things I like to do—short programs, often of a mathematical nature, small utilities to make my life easier, and small computer games. In fact, the things I cover in the book are the things that I have found most useful or interesting in my programming experience, and this book serves partly to document those things for myself. This book is not designed as a thorough preparation for a career in software engineering. Interested readers should progress from this book to a book that has more on computer science and the design and organization of large programs.
In terms of structuring a course around this book or learning on your own, the basis is most of Part I. The first four chapters are critically important. Chapter 5 is useful, but not all of it is critical. Chapter 6 (strings) should be done before Chapter 7 (lists). Chapter 8 contains some more advanced list topics. Much of this can be skipped, though it is all interesting and useful. In particular, that chapter covers list comprehensions, which I use extensively later in the book. While you can get away without using list comprehensions, they provide an elegant and efficient way of doing things. Chapter 9 (while loops) is important. Chapter 10 contains a bunch of miscellaneous topics, all of which are useful, but many can be skipped if need be. The final four chapters of Part I are about dictionaries, text files, functions, and object-oriented programming.
Part II is about graphics, mostly GUI programming with Tkinter. You can very quickly write some nice programs using Tkinter. For instance, this section presents a 20-line working (though not perfect) tic-tac-toe game. The final chapter of Part II covers a bit about the Python Imaging Library.
Part III contains a lot of the fun and interesting things you can do with Python. If you are structuring a one-semester course around this book, you might want to pick a few topics in Part III to go over. This part of the book could also serve as a reference or as a place for interested and motivated students to learn more. All of the topics in this part of the book are things that I have found useful at one point or another.
Though this book was designed to be used in an introductory programming course, it is also useful for those with prior programming experience looking to learn Python. If you are one of those people, you should be able to breeze through the first several chapters. You should find Part II to be a concise, but not superficial, treatment on GUI programming. Part III contains information on the features of Python that allow you to accomplish big things with surprisingly little code.
In preparing this book the Python documentation was indispensable.
Text files used in the text and exercises are available here.
Please send comments, corrections, and suggestions to heinold@msmary.edu.
PART I: BASICS
Getting Started
This chapter will get you up and running with Python, from downloading it to writing simple programs.
Installing Python
Go to python.org and download the latest version of Python (version 3.5 as of this writing). It should be painless to install. If you have a Mac or Linux, you may already have Python on your computer, though it may be an older version. If it is version 2.7 or earlier, then you should install the latest version, as many of the programs in this book will not work correctly on older versions.
IDLE
IDLE is a simple integrated development environment (IDE) that comes with Python. It's a program that allows you to type in your programs and run them. There are other IDEs for Python, but for now I would suggest sticking with IDLE as it is simple to use. You can find IDLE in the Python 3.4 folder on your computer.
When you first start IDLE, it starts up in the shell, which is an interactive window where you can type in Python code and see the output in the same window. I often use the shell in place of my calculator or to try out small pieces of code. But most of the time you will want to open up a new window and type the program in there.
Note
At least on Windows, if you click on a Python file on your desktop, your system will run the program, but not show the code, which is probably not what you want. Instead, if you right-click on the file, there should be an option called Edit with Idle. To edit an existing Python file, either do that or start up IDLE and open the file through the File menu.
Keyboard shortcuts
The following keystrokes work in IDLE and can really speed up your work.
| Keystroke | Result |
|---|---|
CTRL+C | Copy selected text |
CTRL+X | Cut selected text |
CTRL+V | Paste |
CTRL+Z | Undo the last keystroke or group of keystrokes |
CTRL+SHIFT+Z | Redo the last keystroke or group of keystrokes |
F5 | Run module |
A first program
Start IDLE and open up a new window (choose New Window under the File Menu). Type in the following program.
temp = eval(input('Enter a temperature in Celsius: '))
print('In Fahrenheit, that is', 9/5*temp+32)
Then, under the Run menu, choose Run Module (or press F5). IDLE will ask you to save the file, and you should do so. Be sure to append
.py to the filename as IDLE will not automatically append it. This will tell IDLE to use colors to make your program easier to read.
Once you've saved the program, it will run in the shell window. The program will ask you for a temperature. Type in 20 and press enter. The program's output looks something like this:
Enter a temperature in Celsius: 20 In Fahrenheit, that is 68.0
Let's examine how the program does what it does. The first line asks the user to enter a temperature. The input function's job is to ask the user to type something in and to capture what the user types. The part in quotes is the prompt that the user sees. It is called a eval function is something we use here, but it won't be clear exactly why until later. So for now, just remember that we use it when we're getting numerical input.
We need to give a name to the value that the user enters so that the program can remember it and use it in the second line. The name we use is temp and we use the equals sign to assign the user's value to temp.
The second line uses the print function to print out the conversion. The part in quotes is another string and will appear to your program's user exactly as it appears in quotes here. The second argument to the print function is the calculation. Python will do the calculation and print out the numerical result.
This program may seem too short and simple to be of much use, but there are many websites that have little utilities that do similar conversions, and their code is not much more complicated than the code here.
A second program
Here is a program that computes the average of two numbers that the user enters:
num1 = eval(input('Enter the first number: '))
num2 = eval(input('Enter the second number: '))
print('The average of the numbers you entered is', (num1+num2)/2)
For this program we need to get two numbers from the user. There are ways to do that in one line, but for now we'll keep things simple. We get the numbers one at a time and give each number its own name. The only other thing to note is the parentheses in the average calculation. This is because of the order of operations. All multiplications and divisions are performed before any additions and subtractions, so we have to use parentheses to get Python to do the addition first.
Typing things in
Case
Case matters. To Python,print, Print, and PRINT are all different things. For now, stick with lowercase as most Python statements are in lowercase.
Spaces
Spaces matter at the beginning of lines, but not elsewhere. For example, the code below will not work.
temp = eval(input('Enter a temperature in Celsius: '))
print('In Fahrenheit, that is', 9/5*temp+32)
Python uses indentation of lines for things we'll learn about soon. On the other hand, spaces in most other places don't matter. For instance, the following lines have the same effect:
print('Hello world!')
print ('Hello world!')
print( 'Hello world!' )
Basically, computers will only do what you tell them, and they often take things very literally. Python itself totally relies on things like the placement of commas and parentheses so it knows what's what. It is not very good at figuring out what you mean, so you have to be precise. It will be very frustrating at first, trying to get all of the parentheses and commas in the right places, but after a while it will become more natural. Still, even after you've programmed for a long time, you will still miss something. Fortunately, the Python interpreter is pretty good about helping you find your mistakes.
Getting input
The input function is a simple way for your program to get information from people using your program. Here is an example:
name = input('Enter your name: ')
print('Hello, ', name)
The basic structure is
<variable name> = input(<message to user>)
The above works for getting text from the user. To get numbers from the user to use in calculations, we need to do something extra. Here is an example:
num = eval(input('Enter a number: '))
print('Your number squared:', num*num)
The eval function converts the text entered by the user into a number. One nice feature of this is you can enter expressions, like 3*12+5, and eval will compute them for you.
Note
If you run your program and nothing seems to be happening, try pressing enter. There is a bit of a glitch in IDLE that occasionally happens with input statements.
Printing
Here is a simple example:
print('Hi there')
The print function requires parenthesis around its arguments. In the program above, its only argument is the string 'Hi there'. Anything inside quotes will (with a few exceptions) be printed exactly as it appears. In the following, the first statement will output 3+4, while the second will output 7.
print('3+4')
print(3+4)
To print several things at once, separate them by commas. Python will automatically insert spaces between them. Below is an example and the output it produces.
print('The value of 3+4 is', 3+4)
print('A', 1, 'XYZ', 2)
The value of 3+4 is 7 A 1 XYZ 2
Optional arguments
There are two optional arguments to the print function. They are not overly important at this stage of the game, so you can safely skip over this section, but they are useful for making your output look nice.
sep
Python will insert a space between each of the arguments of the print function. There is an optional argument called sep, short
for separator, that you can use to change that space to something else. For example, using sep=':' would separate the arguments
by a colon and sep='##' would separate the arguments by two pound signs.
One particularly useful possibility is to have nothing inside the quotes, as in sep=''. This says to put no separation between the arguments. Here is an example where sep is useful for getting the output to look nice:
print ('The value of 3+4 is', 3+4, '.')
print ('The value of 3+4 is ', 3+4, '.', sep='')
The value of 3+4 is 7 . The value of 3+4 is 7.
end
The print function will automatically advance to the next line. For instance, the following will print on two lines:
print('On the first line')
print('On the second line')
On the first line On the second line
There is an optional argument called end that you can use to keep the print function from advancing to the next line. Here is an example:
print('On the first line', end='')
print('On the second line')
On the first lineOn the second line
Of course, this could be accomplished better with a single print, but we will see later that there are interesting uses for the end argument.
Variables
Looking back at our first program, we see the use of a variable called temp:
temp = eval(input('Enter a temperature in Celsius: '))
print('In Fahrenheit, that is', 9/5*temp+32)
One of the major purposes of a variable is to remember a value from one part of a program so that it can be used in another part of the program. In the case above, the variable temp stores the value that the user enters so that we can do a calculation with it in the next line.
In the example below, we perform a calculation and need to use the result of the calculation in several places in the program. If we save the result of the calculation in a variable, then we only need to do the calculation once. This also helps to make the program more readable.
temp = eval(input('Enter a temperature in Celsius: '))
f_temp = 9/5*temp+32
print('In Fahrenheit, that is', f_temp)
if f_temp > 212:
print('That temperature is above the boiling point.')
if f_temp < 32:
print('That temperature is below the freezing point.')
We haven't discussed if statements yet, but they do exactly what you think they do.
A second example
Here is another example with variables. Before reading on, try to figure out what the values of x and y will be after the code is executed.
x=3 y=4 z=x+y z=z+1 x=y y=5
After these four lines of code are executed, x is 4, y is 5 and z is 8. One way to understand something like this is to take it one line at a time. This is an especially useful technique for trying to understand more complicated chunks of code. Here is a description of what happens in the code above:
-
xstarts with the value 3 andystarts with the value 4. - In line 3, a variable
zis created to equalx+y, which is 7. - Then the value of
zis changed to equal one more than it currently equals, changing it from 7 to 8. - Next,
xis changed to the current value ofy, which is 4. - Finally,
yis changed to 5. Note that this does not affectx. - So at the end,
xis 4,yis 5, andzis 8.
Variable names
There are just a couple of rules to follow when naming your variables.
- Variable names can contain letters, numbers, and the underscore.
- Variable names cannot contain spaces.
- Variable names cannot start with a number.
- Case matters—for instance,
tempandTempare different.
It helps make your program more understandable if you choose names that are descriptive, but not so long that they clutter up your program.
Exercises
- Print a box like the one below.
******************* ******************* ******************* *******************
- Print a box like the one below.
******************* * * * * *******************
- Print a triangle like the one below.
* ** *** ****
- Write a program that computes and prints the result of the following expression. It is roughly .1017.
512-282
47·48+5 - Ask the user to enter a number. Print out the square of the number, but use the
sepoptional argument to print it out in a full sentence that ends in a period. Sample output is shown below.Enter a number: 5 The square of 5 is 25.
- Ask the user to enter a number x. Use the
sepoptional argument to print out x, 2x, 3x, 4x, and 5x, each separated by three dashes, like below.Enter a number: 7 7---14---21---28---35
- Write a program that asks the user for a weight in kilograms and converts it to pounds. There are 2.2 pounds in a kilogram.
- Write a program that asks the user to enter three numbers (use three separate input statements). Create variables called
totalandaveragethat hold the sum and average of the three numbers and print out the values oftotalandaverage. - A lot of cell phones have tip calculators. Write one. Ask the user for the price of the meal and the percent tip they want to leave. Then print both the tip amount and the total bill with the tip included.
For loops
Probably the most powerful thing about computers is that they can repeat things over and over very quickly. There are several ways to repeat things in Python, the most common of which is the for loop.
Examples
Example 1
The following program will printHello ten times:
for i in range(10):
print('Hello')
The structure of a for loop is as follows:
forvariable name in range(number of times to repeat):
statements to be repeated
The syntax is important here. The word for must be in lowercase, the first line must end with a colon, and the statements to be repeated must be indented. Indentation is used to tell Python which statements will be repeated.
Example 2
The program below asks the user for a number and prints its square, then asks for another number and prints its square, etc. It does this three times and then prints that the loop is done.
for i in range(3):
num = eval(input('Enter a number: '))
print ('The square of your number is', num*num)
print('The loop is now done.')
Enter a number: 3 The square of your number is 9 Enter a number: 5 The square of your number is 25 Enter a number: 23 The square of your number is 529 The loop is now done.
Since the second and third lines are indented, Python knows that these are the statements to be repeated. The fourth line is not indented, so it is not part of the loop and only gets executed once, after the loop has completed.
Looking at the above example, we see where the term for loop comes from: we can picture the execution of the code as starting at the for statement, proceeding to the second and third lines, then looping back up to the for statement.
Example 3
The program below will print A, then B, then it will alternate C's and D's five times and then finish with the letter E once.
print('A')
print('B')
for i in range(5):
print('C')
print('D')
print('E')
The first two print statements get executed once, printing an A followed by a B. Next, the C's and D's alternate five times. Note that we don't get five C's followed by five D's. The way the loop works is we print a C, then a D, then loop back to the start of the loop and print a C and another D, etc. Once the program is done looping with the C's and D's, it prints one E.
Example 4
If we wanted the above program to print five C's followed by five D's, instead of alternating C's and D's, we could do the following:
print('A')
print('B')
for i in range(5):
print('C')
for i in range(5):
print('D')
print('E')
The loop variable
There is one part of a for loop that is a little tricky, and that is the loop variable. In the example below, the loop variable is the variable i. The output of this program will be the numbers 0, 1, …, 99, each printed on its own line.
for i in range(100):
print(i)
When the loop first starts, Python sets the variable i to 0. Each time we loop back up, Python increases the value of i by 1. The program loops 100 times, each time increasing the value of i by 1, until we have looped 100 times. At this point the value of i is 99.
You may be wondering why i starts with 0 instead of 1. Well, there doesn't seem to be any really good reason why other than that starting at 0 was useful in the early days of computing and it has stuck with us. In fact most things in computer programming start at 0 instead of 1. This does take some getting used to.
Since the loop variable, i, gets increased by 1 each time through the loop, it can be used to keep track of where we are in the looping process. Consider the example below:
for i in range(3):
print(i+1, '-- Hello')
1 -- Hello 2 -- Hello 3 -- Hello
Names
There's nothing too special about the namei for our variable. The programs below will have the exact same result.
for i in range(100): for wacky_name in range(100):
print(i) print(wacky_name)
It's a convention in programming to use the letters i, j, and k for loop variables, unless there's a good reason to give the variable a more descriptive name.
The range function
The value we put in the range function determines how many times we will loop. The way range works is it produces a list of numbers from zero to the value minus one. For instance, range(5) produces five values: 0, 1, 2, 3, and 4.
If we want the list of values to start at a value other than 0, we can do that by specifying the starting value. The statement range(1,5) will produce the list 1, 2, 3, 4. This brings up one quirk of the range function—it stops one short of where we think it should. If we wanted the list to contain the numbers 1 through 5 (including 5), then we would have to do range(1,6).
Another thing we can do is to get the list of values to go up by more than one at a time. To do this, we can specify an optional step as the third argument. The statement range(1,10,2) will step through the list by twos, producing 1, 3, 5, 7, 9.
To get the list of values to go backwards, we can use a step of -1. For instance, range(5,1,-1) will produce the values 5, 4, 3, 2, in that order. (Note that the range function stops one short of the ending value 1). Here are a few more examples:
| Statement | Values generated |
|---|---|
range(10) | 0,1,2,3,4,5,6,7,8,9 |
range(1,10) | 1,2,3,4,5,6,7,8,9 |
range(3,7) | 3,4,5,6 |
range(2,15,3) | 2,5,8,11,14 |
range(9,2,-1) | 9,8,7,6,5,4,3 |
Here is an example program that counts down from 5 and then prints a message.
for i in range(5,0,-1):
print(i, end=' ')
print('Blast off!!')
5 4 3 2 1 Blast off!!!
The end=' ' just keeps everything on the same line.
A Trickier Example
Let's look at a problem where we will make use of the loop variable. The program below prints a rectangle of stars that is 4 rows tall and 6 rows wide.
for i in range(4):
print('*'*6)
The rectangle produced by this code is shown below on the left. The code '*'*6 is something we'll cover in this section; it just repeats the asterisk character six times.
****** * ****** ** ****** *** ****** ****
Suppose we want to make a triangle instead. We can accomplish this with a very small change to the rectangle program. Looking at the program, we can see that the for loop will repeat the print statement four times, making the shape four rows tall. It's the 6 that will need to change.
The key is to change the 6 to i+1. Each time through the loop the program will now print i+1 stars instead of 6 stars. The loop counter variable i runs through the values 0, 1, 2, and 3. Using it allows us to vary the number of stars. Here is triangle program:
for i in range(4):
print('*'*(i+1))
Exercises
- Write a program that prints your name 100 times.
- Write a program to fill the screen horizontally and vertically with your name. [Hint: add the option
end=' 'into theprintfunction to fill the screen horizontally.] - Write a program that outputs 100 lines, numbered 1 to 100, each with your name on it. The output should look like the output below.
1 Your name 2 Your name 3 Your name 4 Your name ... 100 Your name
- Write a program that prints out a list of the integers from 1 to 20 and their squares. The output should look like this:
1 --- 1 2 --- 4 3 --- 9 ... 20 --- 400
- Write a program that uses a for loop to print the numbers 8, 11, 14, 17, 20, …, 83, 86, 89.
- Write a program that uses a for loop to print the numbers 100, 98, 96, …, 4, 2.
- Write a program that uses exactly four for loops to print the sequence of letters below.
AAAAAAAAAABBBBBBBCDCDCDCDEFFFFFFG
- Write a program that asks the user for their name and how many times to print it. The program should print out the user's name the specified number of times.
- The Fibonacci numbers are the sequence below, where the first two numbers are 1, and each number thereafter is the sum of the two preceding numbers. Write a program that asks the user how many Fibonacci numbers to print and then prints that many.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
- Use a for loop to print a box like the one below. Allow the user to specify how wide and how high the box should be. [Hint:
print('*' * 10)prints ten asterisks.]******************* ******************* ******************* *******************
- Use a for loop to print a box like the one below. Allow the user to specify how wide and how high the box should be.
******************* * * * * *******************
- Use a for loop to print a triangle like the one below. Allow the user to specify how high the triangle should be.
* ** *** ****
- Use a for loop to print an upside down triangle like the one below. Allow the user to specify how high the triangle should be.
**** *** ** *
- Use for loops to print a diamond like the one below. Allow the user to specify how high the diamond should be.
* *** ***** ******* ***** *** *
- Write a program that prints a giant letter A like the one below. Allow the user to specify how large the letter should be.
* * * ***** * * * *
Numbers
This chapter focuses on numbers and simple mathematics in Python.
Integers and Decimal Numbers
Because of the way computer chips are designed, integers and decimal numbers are represented differently on computers. Decimal numbers are represented by what are called floating point numbers. The important thing to remember about them is you typically only get about 15 or so digits of precision. It would be nice if there were no limit to the precision, but calculations run a lot more quickly if you cut off the numbers at some point.
On the other hand, integers in Python have no restrictions. They can be arbitrarily large.
For decimal numbers, the last digit is sometimes slightly off due to the fact that computers work in binary (base 2) whereas our human number system is base 10. As an example, mathematically, we know that the decimal expansion of 7/3 is 2.333…, with the threes repeating forever. But when we type 7/3 into the Python shell, we get 2.3333333333333335. This is called roundoff error. For most practical purposes this is not too big of a deal, but it actually can cause problems for some mathematical and scientific calculations. If you really need more precision, there are ways. See this section.
Math Operators
Here is a list of the common operators in Python:
| Operator | Description |
|---|---|
+ | addition |
- | subtraction |
* | multiplication |
/ | division |
** | exponentiation |
// | integer division |
% | modulo (remainder) |
Exponentiation
Python uses** for exponentiation. The caret, ^, is used for something else.
Integer division
The integer division operator,//, requires some explanation. Basically, for positive numbers it behaves like ordinary division except that it throws away the decimal part of the result. For instance, while 8/5 is 1.6, we have 8//5 equal to 1. We will see uses for this operator later. Note that in many other programming languages and in older versions of Python, the usual division operator / actually does integer division on integers.
Modulo
The modulo operator,%, returns the remainder from a division. For instance, the result of 18%7 is 4 because 4 is the remainder when 18 is divided by 7. This operation is surprisingly useful. For instance, a number is divisible by n precisely when it leaves a remainder of 0 when divided by n. Thus to check if a number, n, is even, see if n%2 is equal to 0. To check if n is divisible by 3, see if n%3 is 0.
One use of this is if you want to schedule something in a loop to happen only every other time through the loop, you could check to see if the loop variable modulo 2 is equal to 0, and if it is, then do that something.
The modulo operator shows up surprisingly often in formulas. If you need to “wrap around” and come back to the start, the modulo is useful. For example, think of a clock. If you go six hours past 8 o'clock, the result is 2 o'clock. Mathematically, this can be accomplished by doing a modulo by 12. That is, (8+6)%12 is equal to 2.
As another example, take a game with players 1 through 5. Say you have a variable player that keeps track of the current player. After player 5 goes, it's player 1's turn again. The modulo operator can be used to take care of this:
player = player%5+1
When player is 5, player%5 will be 0 and expression will set player to 1.
Order of operations
Exponentiation gets done first, followed by multiplication and division (including // and %), and addition and subtraction come last. The classic math class mnemonic, PEMDAS (Please Excuse My Dear Aunt Sally), might be helpful.
This comes into play in calculating an average. Say you have three variables x, y, and z, and you want to calculate the average of their values. To expression x+y+z/3 would not work. Because division comes before addition, you would actually be calculating
x+y+z
3
instead of
x+y+z
3.
This is easily fixed by using parentheses: (x+y+z)/3.
In general, if you're not sure about something, adding parentheses might help and usually doesn't do any harm.
Random numbers
To make an interesting computer game, it's good to introduce some randomness into it. Python comes with a module, called
random, that allows us to use random numbers in our programs.
Before we get to random numbers, we should first explain what a module is. The core part of the Python language consists of things like for loops, if statements, math operators, and some functions, like print and input. Everything else is contained in modules, and if we want to use something from a module we have to first import it—that is, tell Python that we want to use it.
At this point, there is only one function, called randint, that we will need from the random module. To load this function, we use the following statement:
from random import randint
Using randint is simple: randint(a,b) will return a random integer between a and b including both a and b. (Note that randint includes the right endpoint b unlike the range function). Here is a short example:
from random import randint
x = randint(1,10)
print('A random number between 1 and 10: ', x)
A random number between 1 and 10: 7
The random number will be different every time we run the program.
Math functions
The math module
Python has a module called math that contains familiar math functions, including sin, cos, tan, exp, log, log10, factorial, sqrt, floor, and ceil. There are also the inverse trig functions, hyperbolic functions, and the constants pi and e. Here is a short example:
from math import sin, pi
print('Pi is roughly', pi)
print('sin(0) =', sin(0))
Pi is roughly 3.14159265359 sin(0) = 0.0
Built-in math functions
There are two built in math functions, abs (absolute value) and round that are available without importing the math module. Here are some examples:
print(abs(-4.3)) print(round(3.336, 2)) print(round(345.2, -1))
4.3 3.34 350.0
The round function takes two arguments: the first is the number to be rounded and the second is the number of decimal places to round to. The second argument can be negative.
Getting help from Python
There is documentation built into Python. To get help on the math module, for example, go to the Python shell and type the following two lines:
>>> import math >>> dir(math)
['__doc__', '__name__', '__package__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'ceil', 'copysign', 'cos', 'cosh', 'degrees', 'e', 'exp', 'fabs', 'factorial', 'floor', 'fmod', 'frexp', 'fsum', 'hypot', 'isinf', 'isnan', 'ldexp', 'log', 'log10', 'log1p', 'modf', 'pi', 'pow', 'radians', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'trunc']
This gives a list of all the functions and variables in the math module. You can ignore all of the ones that start with underscores. To get help on a specific function, say the floor function, you can type help(math.floor). Typing help(math) will give you help for everything in the math module.
Using the Shell as a Calculator
The Python shell can be used as a very handy and powerful calculator. Here is an example session:
>>> 23**2
529
>>> s = 0
>>> for n in range(1,10001):
s = s + 1/n**2
>>> s
1.6448340718480652
>>> from math import *
>>> factorial(10)
3628800
The second example here sums the numbers 1+1/4+1/9+…+1/100002. The result is stored in the variable s. To inspect the value of that variable, just type its name and press enter. Inspecting variables is useful for debugging your programs. If a program is not working properly, you can type your variable names into the shell after the program has finished to see what their values are.
The statement from math import * imports every function from the math module, which can make the shell a lot like a scientific calculator.
Note
Under the Shell menu, selectRestart shell if you want to clear the values of all the variables.
Exercises
- Write a program that generates and prints 50 random integers, each between 3 and 6.
- Write a program that generates a random number, x, between 1 and 50, a random number y between 2 and 5, and computes xy.
- Write a program that generates a random number between 1 and 10 and prints your name that many times.
- Write a program that generates a random decimal number between 1 and 10 with two decimal places of accuracy. Examples are 1.23, 3.45, 9.80, and 5.00.
- Write a program that generates 50 random numbers such that the first number is between 1 and 2, the second is between 1 and 3, the third is between 1 and 4, …, and the last is between 1 and 51.
- Write a program that asks the user to enter two numbers, x and y, and computes |x-y|/(x+y).
- Write a program that asks the user to enter an angle between -180° and 180°. Using an expression with the modulo operator, convert the angle to its equivalent between 0° and 360°.
- Write a program that asks the user for a number of seconds and prints out how many minutes and seconds that is. For instance, 200 seconds is 3 minutes and 20 seconds. [Hint: Use the
//operator to get minutes and the%operator to get seconds.] - Write a program that asks the user for an hour between 1 and 12 and for how many hours in the future they want to go. Print out what the hour will be that many hours into the future. An example is shown below.
Enter hour: 8 How many hours ahead? 5 New hour: 1 o'clock
-
- One way to find out the last digit of a number is to mod the number by 10. Write a program that asks the user to enter a power. Then find the last digit of 2 raised to that power.
- One way to find out the last two digits of a number is to mod the number by 100. Write a program that asks the user to enter a power. Then find the last two digits of 2 raised to that power.
- Write a program that asks the user to enter a power and how many digits they want. Find the last that many digits of 2 raised to the power the user entered.
- Write a program that asks the user to enter a weight in kilograms. The program should convert it to pounds, printing the answer rounded to the nearest tenth of a pound.
- Write a program that asks the user for a number and prints out the factorial of that number.
- Write a program that asks the user for a number and then prints out the sine, cosine, and tangent of that number.
- Write a program that asks the user to enter an angle in degrees and prints out the sine of that angle.
- Write a program that prints out the sine and cosine of the angles ranging from 0 to 345° in 15° increments. Each result should be rounded to 4 decimal places. Sample output is shown below:
0 --- 0.0 1.0 15 --- 0.2588 0.9659 30 --- 0.5 0.866 ... 345 --- -0.2588 0.9659
-
Below is described how to find the date of Easter in any year. Despite its intimidating appear-
ance, this is not a hard problem. Note that bxc is the floor function, which for positive numbers
just drops the decimal part of the number. For instance ⌊3.14⌋ = 3. The floor function is part
of the math module.
C = century (1900s → C=19)
Easter is either March (22 + d + e) or April (d + e - 9). There is an exception if d=29 and e=6. In this case, Easter falls one week earlier on April 19. There is another exception if d=28, e=6, and m=2,5,10,13,16,21,24, or 39. In this case, Easter falls one week earlier on April 18. Write a program that asks the user to enter a year and prints out the date of Easter in that year. (See Tattersall, Elementary Number Theory in Nine Chapters, 2nd ed., page 167)
Y = year (all four digits)
m = (15+C-⌊C/4⌋ - ⌊(8C+13)/25⌋) mod 30
n = (4+C-⌊C/4⌋) mod 7
a = Y mod 4
b = Y mod 7
c = Y mod 19
d = (19c + m) mod 30
e = (2a+4b+6d+n) mod 7 - A year is a leap year if it is divisible by 4, except that years divisible by 100 are not leap years unless they are also divisible by 400. Ask the user to enter a year, and, using the
//operator, determine how many leap years there have been between 1600 and that year. - Write a program that given an amount of change less than $1.00 will print out exactly how many quarters, dimes, nickels, and pennies will be needed to efficiently make that change. [Hint: the
//operator may be useful.] - Write a program that draws “modular rectangles” like the ones below. The user specifies the width and height of the rectangle, and the entries start at 0 and increase typewriter fashion from left to right and top to bottom, but are all done mod 10. Below are examples of a 3 × 5 rectangle and a 4 × 8.
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1
If statements
Quite often in programs we only want to do something provided something else is true. Python's if statement is what we need.
A Simple Example
Let's try a guess-a-number program. The computer picks a random number, the player tries to guess, and the program tells them if they are correct. To see if the player's guess is correct, we need something new, called an if statement.
from random import randint
num = randint(1,10)
guess = eval(input('Enter your guess: '))
if guess==num:
print('You got it!')
The syntax of the if statement is a lot like the for statement in that there is a colon at the end of the if condition and the following line or lines are indented. The lines that are indented will be executed only if the condition is true. Once the indentation is done with, the if block is concluded.
The guess-a-number game works, but it is pretty simple. If the player guesses wrong, nothing happens. We can add to the if statement as follows:
if guess==num:
print('You got it!')
else:
print('Sorry. The number is ', num)
We have added an else statement, which is like an “otherwise.”
Conditional operators
The comparison operators are ==, >, <, >=, <=, and !=. That last one is for not equals. Here are a few examples:
| Expression | Description |
|---|---|
if x>3: | if x is greater than 3 |
if x>=3: | if x is greater than or equal to 3 |
if x==3: | if x is 3 |
if x!=3: | if x is not 3 |
There are three additional operators used to construct more complicated conditions: and, or, and not. Here are
some examples:
if grade>=80 and grade<90:
print('Your grade is a B.')
if score>1000 or time>20:
print('Game over.')
if not (score>1000 or time>20):
print('Game continues.')
Order of operations
In terms of order of operations, and is done before or, so if you have a complicated condition that contains both, you
may need parentheses around the or condition. Think of and as being like multiplication and or as being like addition. Here is an example:
if (score<1000 or time>20) and turns_remaining==0:
print('Game over.')
Common Mistakes
Mistake 1
The operator for equality consists of two equals signs. It is a really common error to forget one of the equals signs.| Incorrect | Correct |
|---|---|
if x=1: | if x==1: |
Mistake 2
A common mistake is to useand where or is needed or vice-versa. Consider the following if statements:
if x>1 and x<100: if x>1 or x<100:
The first statement is the correct one. If x is any value between 1 and 100, then the statement will be
true. The idea is that x has to be both greater than 1 and less than 100. On the other hand, the second statement is not what we want because for it to be true, either x has to be greater than 1 or x has to be less than 100. But every number satisfies this. The lesson here is if your program is not working correctly, check your and's and or's.
Mistake 3
Another very common mistake is to write something like below:if grade>=80 and <90:
This will lead to a syntax error. We have to be explicit. The correct statement is
if grade>=80 and grade<90:
On the other hand, there is a nice shortcut that does work in Python (though not in many other programming languages):
if 80<=grade<90:
elif
A simple use of an if statement is to assign letter grades. Suppose that scores 90 and above are A's, scores in the 80s are B's, 70s are C's, 60s are D's, and anything below 60 is an F. Here is one way to do this:
grade = eval(input('Enter your score: '))
if grade>=90:
print('A')
if grade>=80 and grade<90:
print('B')
if grade>=70 and grade<80:
print('C')
if grade>=60 and grade<70:
print('D')
if grade<60:
print('F')
The code above is pretty straightforward and it works. However, a more elegant way to do it is shown below.
grade = eval(input('Enter your score: '))
if grade>=90:
print('A')
elif grade>=80:
print('B')
elif grade>=70:
print('C')
elif grade>=60:
print('D')
else:
print('F')
With the separate if statements, each condition is checked regardless of whether it really needs to be. That is, if the score is
a 95, the first program will print an A but then continue on and check to see if the score is a B, C, etc.,
which is a bit of a waste. Using elif, as soon as we find where the score matches, we stop checking conditions and skip all
the way to the end of the whole block of statements. An added benefit of this is that the conditions we use in the elif
statements are simpler than in their if counterparts. For instance, when using elif, the second part of the second
if statement condition, grade<90, becomes unnecessary because the corresponding elif does not have to worry
about a score of 90 or above, as such a score would have already been caught by the first if statement.
You can get along just fine without elif, but it can often make your code simpler.
Exercises
- Write a program that asks the user to enter a length in centimeters. If the user enters a negative length, the program should tell the user that the entry is invalid. Otherwise, the program should convert the length to inches and print out the result. There are 2.54 centimeters in an inch.
- Ask the user for a temperature. Then ask them what units, Celsius or Fahrenheit, the temperature is in. Your program should convert the temperature to the other unit. The conversions are F=9/5*C+32 and C=5/9*(F-32).
- Ask the user to enter a temperature in Celsius. The program should print a message based on the temperature:
- If the temperature is less than -273.15, print that the temperature is invalid because it is below absolute zero.
- If it is exactly -273.15, print that the temperature is absolute 0.
- If the temperature is between -273.15 and 0, print that the temperature is below freezing.
- If it is 0, print that the temperature is at the freezing point.
- If it is between 0 and 100, print that the temperature is in the normal range.
- If it is 100, print that the temperature is at the boiling point.
- If it is above 100, print that the temperature is above the boiling point.
-
Write a program that asks the user how many credits they have taken. If they have taken 23 or less, print that the student is a freshman. If they have taken between 24 and 53, print that they are a sophomore. The range for juniors is 54 to 83, and for seniors it is 84 and over.
- Generate a random number between 1 and 10. Ask the user to guess the number and print a message based on whether they get it right or not.
- A store charges $12 per item if you buy less than 10 items. If you buy between 10 and 99 items, the cost is $10 per item. If you buy 100 or more items, the cost is $7 per item. Write a program that asks the user how many items they are buying and prints the total cost.
-
Write a program that asks the user for two numbers and prints
Closeif the numbers are within .001 of each other andNotcloseotherwise. - A year is a leap year if it is divisible by 4, except that years divisible by 100 are not leap years unless they are also divisible by 400. Write a program that asks the user for a year and prints out whether it is a leap year or not.
-
Write a program that asks the user to enter a number and prints out all the divisors of that number. [Hint: the
%operator is used to tell if a number is divisible by something. See this_section.] - Write a multiplication game program for kids. The program should give the player ten randomly generated multiplication questions to do. After each, the program should tell them whether they got it right or wrong and what the correct answer is.
Question 1: 3 x 4 = 12 Right! Question 2: 8 x 6 = 44 Wrong. The answer is 48. ... ... Question 10: 7 x 7 = 49 Right.
- Write a program that asks the user for an hour between 1 and 12, asks them to enter
amorpm, and asks them how many hours into the future they want to go. Print out what the hour will be that many hours into the future, printingamorpmas appropriate. An example is shown below.Enter hour: 8 am (1) or pm (2)? 1 How many hours ahead? 5 New hour: 1 pm
- A jar of Halloween candy contains an unknown amount of candy and if you can guess exactly how much candy is in the bowl, then you win all the candy. You ask the person in charge the following: If the candy is divided evenly among 5 people, how many pieces would be left over? The answer is 2 pieces. You then ask about dividing the candy evenly among 6 people, and the amount left over is 3 pieces. Finally, you ask about dividing the candy evenly among 7 people, and the amount left over is 2 pieces. By looking at the bowl, you can tell that there are less than 200 pieces. Write a program to determine how many pieces are in the bowl.
- Write a program that lets the user play Rock-Paper-Scissors against the computer. There should be five rounds, and after those five rounds, your program should print out who won and lost or that there is a tie.
Miscellaneous Topics I
This chapter consists of a several common techniques and some other useful information.
Counting
Very often we want our programs to count how many times something happens. For instance, a video game may need to keep track of how many turns a player has used, or a math program may want to count how many numbers have a special property. The key to counting is to use a variable to keep the count.
Example 1
This program gets 10 numbers from the user and counts how many of those numbers are greater than 10.
count = 0
for i in range(10):
num = eval(input('Enter a number: '))
if num>10:
count=count+1
print('There are', count, 'numbers greater than 10.')
Think of the count variable as if we are keeping a tally on a piece of paper. Every time we get a number larger than 10, we add 1 to our tally. In the program, this is accomplished by the line count=count+1. The first line of the program, count=0, is important. Without it, the Python interpreter would get to the count=count+1 line and spit out an error saying something about not knowing what count is. This is because the first time the program gets to this line, it tries to do what it says: take the old value of count, add 1 to it, and store the result in count. But the first time the program gets there, there is no old value of count to use, so the Python interpreter doesn't know what to do. To avoid the error, we need to define count, and that is what the first line does. We set it to 0 to indicate that at the start of the program no numbers greater than 10 have been found.
Counting is an extremely common thing. The two things involved are:
-
count=0— Start the count at 0. -
count = count + 1— Increase the count by 1.
Example 2
This modification of the previous example counts how many of the numbers the user enters are greater than 10 and also how many are equal to 0. To count two things we use two count variables.
count1 = 0
count2 = 0
for i in range(10):
num = eval(input('Enter a number: '))
if num>10:
count1=count1+1
if num==0:
count2=count2+1
print('There are', count1, 'numbers greater than 10.')
print('There are', count2, 'zeroes.')
Example 3
Next we have a slightly trickier example. This program counts how many of the squares from 12 to 1002 end in a 4.
count = 0
for i in range(1,101):
if (i**2)%10==4:
count = count + 1
print(count)
A few notes here: First, because of the aforementioned quirk of the range function, we need to use range(1,101) to loop through the numbers 1 through 100. The looping variable i takes on those values, so the squares from 12 to 1002 are represented by i**2. Next, to check if a number ends in 4, a nice mathematical trick is to check if it leaves a remainder of 4 when divided by 10. The modulo operator, %, is used to get the remainder.
Summing
Closely related to counting is summing, where we want to add up a bunch of numbers.
Example 1
This program will add up the numbers from 1 to 100. The way this works is that each time we encounter a new number, we add it to our running total,s.
s = 0
for i in range(1,101):
s = s + i
print('The sum is', s)
Example 2
This program that will ask the user for 10 numbers and then computes their average.
s = 0
for i in range(10):
num = eval(input('Enter a number: '))
s = s + num
print('The average is', s/10)
Example 3
A common use for summing is keeping score in a game. Near the beginning of the game we would set the score variable equal to 0. Then when we want to add to the score we would do something like below:
score = score + 10
Swapping
Quite often we will want to swap the values of two variables, x and y. It would be tempting to try the following:
x = y y = x
But this will not work. Suppose x is 3 and y is 5. The first line will set x to 5, which is good, but then the second line will set y to 5 also because x is now 5. The trick is to use a third variable to save the value of x:
hold = x x = y y = hold
In many programming languages, this is the usual way to swap variables. Python, however, provides a nice shortcut:
x,y = y,x
We will learn later exactly why this works. For now, feel free to use whichever method you prefer. The latter method, however, has the advantage of being shorter and easier to understand.
Flag variables
A flag variable can be used to let one part of your program know when something happens in another part of the program. Here is an example that determines if a number is prime.
num = eval(input('Enter number: '))
flag = 0
for i in range(2,num):
if num%i==0:
flag = 1
if flag==1:
print('Not prime')
else:
print('Prime')
Recall that a number is prime if it has no divisors other than 1 and itself. The way the program above works is flag starts off at 0. We then loop from 2 to num-1. If one of those values turns out to be a divisor, then flag gets set to 1. Once the loop is finished, we check to see if the flag got set or not. If it did, we know there was a divisor, and num isn't prime. Otherwise, the number must be prime.
Maxes and mins
A common programming task is to find the largest or smallest value in a series of values. Here is an example where we ask the user to enter ten positive numbers and then we print the largest one.
largest = eval(input('Enter a positive number: '))
for i in range(9):
num = eval(input('Enter a positive number: '))
if num>largest:
largest=num
print('Largest number:', largest)
The key here is the variable largest that keeps track of the largest number found so far. We start by setting it equal to the user's first number. Then, every time we get a new number from the user, we check to see if the user's number is larger than the current largest value (which is stored in largest). If it is, then we set largest equal to the user's number.
If, instead, we want the smallest value, the only change necessary is that > becomes <, though it would also be good to rename the variable largest to smallest.
Later on, when we get to lists, we will see a shorter way to find the largest and smallest values, but the technique above is useful to know since you may occasionally run into situations where the list way won't do everything you need it to do.
Comments
A comment is a message to someone reading your program. Comments are often used to describe what a section of code does or how it works, especially with tricky sections of code. Comments have no effect on your program.
Single-line comments
For a single-line comment, use the # character.
# a slightly sneaky way to get two values at once
num1, num2 = eval(input('Enter two numbers separated by commas: '))
You can also put comments at the end of a line:
count = count + 2 # each divisor contributes two the count
Multi-line comments
For comments that span several lines, you can use triple quotes.
""" Program name: Hello world
Author: Brian Heinold
Date: 1/9/11 """
print('Hello world')
One nice use for the triple quotes is to comment out parts of your code. Often you will want to modify your program but don't want to delete your old code in case your changes don't work. You could comment out the old code so that it is still there if you need it, and it will be ignored when your new program is run. Here is a simple example:
"""
print('This line and the next are inside a comment.')
print('These lines will not get executed.')
"""
print('This line is not in a comment and it will be executed.')
Simple debugging
Here are two simple techniques for figuring out why a program is not working:
- Use the Python shell. After your program has run, you can type in the names of your program's variables to inspect their values and see which ones have the values you expect them to have and which don't. You can also use the Shell to type in small sections of your program and see if they are working.
- Add print statements to your program. You can add these at any point in your program to see what the values of your variables are. You can also add a print statement to see if a point in your code is even being reached. For instance, if you think you might have an error in a condition of an if statement, you can put a print statement into the if block to see if the condition is being triggered.
Here is an example from the part of the primes program from earlier in this chapter. We put a print statement into the for loop to see exactly when the flag variable is being set:
flag = 0 num = eval(input('Enter number: ')) for i in range(2,num): if num%i==0: flag = 1 print(i, flag) - An empty input statement, like below, can be used to pause your program at a specific point:
input()
Example programs
It is a valuable skill is to be able to read code. In this section we will look in depth at some simple programs and try to understand how they work.
Example 1
The following program prints Hello a random number of times between 5 and 25.
from random import randint
rand_num = randint(5,25)
for i in range(rand_num):
print('Hello')
The first line in the program is the import statement. This just needs to appear once, usually near the beginning of your program. The next line generates a random number between 5 and 25. Then, remember that to repeat something a specified number of times, we use a for loop. To repeat something 50 times, we would use range(50) in our for loop. To repeat something 100 times, we would use range(100). To repeat something a random number of times, we can use range(rand_num), where
rand_num is a variable holding a random number. Although if we want, we can skip the variable and put the randint statement directly in the range function, as shown below.
from random import randint
for i in range(randint(5,25)):
print('Hello')
Example 2
Compare the following two programs.
from random import randint from random import randint
rand_num = randint(1,5) for i in range(6):
for i in range(6): rand_num = randint(1,5)
print('Hello'*rand_num) print('Hello'*rand_num)
Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello
The only difference between the programs is in the placement of the rand_num statement. In the first program, it is located outside of the for loop, and this means that rand_num is set once at the beginning of the program and retains that same value for the life of the program. Thus every print statement will print Hello the same number of times. In the second program, the rand_num statement is within the loop. Right before each print statement, rand_num is assigned a new random number, and so the number of times Hello is printed will vary from line to line.
Example 3
Let us write a program that generates 10000 random numbers between 1 and 100 and counts how many of them are multiples of 12. Here are the things we will need:- Because we are using random numbers, the first line of the program should import the
randommodule. - We will require a for loop to run 10000 times.
- Inside the loop, we will need to generate a random number, check to see if it is divisible by 12, and if so, add 1 to the count.
- Since we are counting, we will also need to set the count equal to 0 before we start counting.
- To check divisibility by 12, we use the modulo,
%, operator.
When we put this all together, we get the following:
from random import randint
count = 0
for i in range(10000):
num = randint(1, 100)
if num%12==0:
count=count+1
print('Number of multiples of 12:', count)
Indentation matters
A common mistake is incorrect indentation. Suppose we take the above and indent the last line. The program will still run, but it won't run as expected.
from random import randint
count = 0
for i in range(10000):
num = randint(1, 100)
if num%12==0:
count=count+1
print('Number of multiples of 12:', count)
When we run it, it outputs a whole bunch of numbers. The reason for this is that by indenting the print statement, we have made it a part of the for loop, so the print statement will be executed 10,000 times.
Suppose we indent the print statement one step further, like below.
from random import randint
count = 0
for i in range(10000):
num = randint(1, 100)
if num%12==0:
count=count+1
print('Number of multiples of 12:', count)
Now, not only is it part of the for loop, but it is also part of the if statement. What will happen is every time we find a new multiple of 12, we will print the count. Neither this, nor the previous example, is what we want. We just want to print the count once at the end of the program, so we don't want the print statement indented at all.
Exercises
- Write a program that counts how many of the squares of the numbers from 1 to 100 end in a 1.
- Write a program that counts how many of the squares of the numbers from 1 to 100 end in a 4 and how many end in a 9.
- Write a program that asks the user to enter a value n, and then computes (1+1/2+1/3+…+1/n)-ln(n). The ln function is
login themathmodule. - Write a program to compute the sum 1-2+3-4+…+1999-2000.
- Write a program that asks the user to enter a number and prints the sum of the divisors of that number. The sum of the divisors of a number is an important function in number theory.
- A number is called a perfect number if it is equal to the sum of all of its divisors, not including the number itself. For instance, 6 is a perfect number because the divisors of 6 are 1, 2, 3, 6 and 6=1+2+3. As another example, 28 is a perfect number because its divisors are 1, 2, 4, 7, 14, 28 and 28=1+2+4+7+14. However, 15 is not a perfect number because its divisors are 1, 3, 5, 15 and 15≠1+3+5. Write a program that finds all four of the perfect numbers that are less than 10000.
- An integer is called squarefree if it is not divisible by any perfect squares other than 1. For instance, 42 is squarefree because its divisors are 1, 2, 3, 6, 7, 21, and 42, and none of those numbers (except 1) is a perfect square. On the other hand, 45 is not squarefree because it is divisible by 9, which is a perfect square. Write a program that asks the user for an integer and tells them if it is squarefree or not.
- Write a program that swaps the values of three variables x, y, and z, so that x gets the value of y, y gets the value of z, and z gets the value of x.
- Write a program to count how many integers from 1 to 1000 are not perfect squares, perfect cubes, or perfect fifth powers.
- Ask the user to enter 10 test scores. Write a program to do the following:
- Print out the highest and lowest scores.
- Print out the average of the scores.
- Print out the second largest score.
- If any of the scores is greater than 100, then after all the scores have been entered, print a message warning the user that a value over 100 has been entered.
- Drop the two lowest scores and print out the average of the rest of them.
- Write a program that computes the factorial of a number. The factorial, n!, of a number n is the product of all the integers between 1 and n, including n. For instance, 5!=1·2·3·4·5=120. [Hint: Try using a multiplicative equivalent of the summing technique.]
- Write a program that asks the user to guess a random number between 1 and 10. If they guess right, they get 10 points added to their score, and they lose 1 point for an incorrect guess. Give the user five numbers to guess and print their score after all the guessing is done.
- In the last chapter there was an exercise that asked you to create a multiplication game for kids. Improve your program from that exercise to keep track of the number of right and wrong answers. At the end of the program, print a message that varies depending on how many questions the player got right.
-
This exercise is about the well-known Monty Hall problem. In the problem, you are a contestant on a game show. The host, Monty Hall, shows you three doors. Behind one of those doors is a prize, and behind the other two doors are goats. You pick a door. Monty Hall, who knows behind which door the prize lies, then opens up one of the doors that doesn't contain the prize. There are now two doors left, and Monty gives you the opportunity to change your choice. Should you keep the same door, change doors, or does it not matter?
- Write a program that simulates playing this game 10000 times and calculates what percentage of the time you would win if you switch and what percentage of the time you would win by not switching.
- Try the above but with four doors instead of three. There is still only one prize, and Monty still opens up one door and then gives you the opportunity to switch.
Strings
Strings are a data type in Python for dealing with text. Python has a number of powerful features for manipulating strings.
Basics
Creating a string
A string is created by enclosing text in quotes. You can use either single quotes, ', or double quotes, ". A triple-quote can be used for multi-line strings. Here are some examples:
s = 'Hello' t = "Hello" m = """This is a long string that is spread across two lines."""
Input
Recall from this chapter that when getting numerical input we use an eval statement with the input statement, but when getting text, we do not use eval. The difference is illustrated below:
num = eval(input('Enter a number: '))
string = input('Enter a string: ')
Empty string
The empty string''; is the string equivalent of the number 0. It is a string with nothing in it. We have seen it before, in the print statement's optional argument, sep='';.
Length
To get the length of a string (how many characters it has), use the built-in functionlen. For example, len('Hello') is 5.
Concatenation and repetition
The operators + and * can be used on strings. The + operator combines two strings. This operation is called concatenation. The * repeats a string a certain number of times. Here are some examples.
| Expression | Result |
|---|---|
'AB'+'cd' | 'ABcd' |
'A'+'7'+'B' | 'A7B' |
'Hi'*4 | 'HiHiHiHi' |
Example 1
If we want to print a long row of dashes, we can do the following
print('-'*75)
Example 2
The+ operator can be used to build up a string, piece by piece, analogously to the way we built up counts and sums in this section and this one. Here is an example that repeatedly asks the user to enter a letter and builds up a string consisting of only the vowels that the user entered.
s = '';
for i in range(10):
t = input('Enter a letter: ')
if t=='a' or t=='e' or t=='i' or t=='o' or t=='u':
s = s + t
print(s)
This technique is very useful.
The in operator
The in operator is used to tell if a string contains something. For example:
if 'a' in string:
print('Your string contains the letter a.')
You can combine in with the not operator to tell if a string does not contain something:
if ';' not in string:
print('Your string does not contain any semicolons.')
Example
In the previous section we had the long if condition
if t=='a' or t=='e' or t=='i' or t=='o' or t=='u':
Using the in operator, we can replace that statement with the following:
if t in 'aeiou':
Indexing
We will often want to pick out individual characters from a string. Python uses square brackets to do this. The table below gives some examples of indexing the string s='Python'.
Statement | Result | Description |
|---|---|---|
s[0] | P | first character of s |
s[1] | y | second character of s |
s[-1] | n | last character of s |
s[-2] | o | second-to-last character of s |
- The first character of
siss[0], nots[1]. Remember that in programming, counting usually starts at 0, not 1. - Negative indices count backwards from the end of the string.
A common error
Suppose s='Python' and we try to do s[12]. There are only six characters in the string and Python will raise the following error message:
IndexError: string index out of range
You will see this message again. Remember that it happens when you try to read past the end of a string.
Slices
A slice is used to pick out part of a string. It behaves like a combination of indexing and the range function. Below we have some examples with the string s='abcdefghij'.
index: 0 1 2 3 4 5 6 7 8 9 letters: a b c d e f g h i j
| Code | Result | Description |
|---|---|---|
s[2:5] | cde | characters at indices 2, 3, 4 |
s[ :5] | abcde | first five characters |
s[5: ] | fghij | characters from index 5 to the end |
s[-2: ] | ij | last two characters |
s[ : ] | abcdefghij | entire string |
s[1:7:2] | bdf | characters from index 1 to 6, by twos |
s[ : :-1] | jihgfedcba | a negative step reverses the string |
- The basic structure is
string name[starting location : ending location+1]
Slices have the same quirk as the
rangefunction in that they do not include the ending location. For instance, in the example above,s[2:5]gives the characters in indices 2, 3, and 4, but not the character in index 5. - We can leave either the starting or ending locations blank. If we leave the starting location blank, it defaults to the start of the string. So
s[:5]gives the first five characters ofs. If we leave the ending location blank, it defaults to the end of the string. Sos[5:]will give all the characters from index 5 to the end. If we use negative indices, we can get the ending characters of the string. For instance,s[-2:]gives the last two characters. - There is an optional third argument, just like in the
rangestatement, that can specify the step. For example,s[1:7:2]steps through the string by twos, selecting the characters at indices 1, 3, and 5 (but not 7, because of the aforementioned quirk). The most useful step is -1, which steps backwards through the string, reversing the order of the characters.
Changing individual characters of a string
Suppose we have a string called s and we want to change the character at index 4 of s to 'X'. It is tempting to try s[4]='X', but that unfortunately will not work. Python strings are immutable, which means we can't modify any part of them. There is more on why this is in this section. Here is code that will change the character at index 4 to 'X':
s = s[:4] + 'X' + s[5:]
The idea of this is we take all the characters up to index 4, then X, and then all of the characters after index 4.
Looping
Very often we will want to scan through a string one character at a time. A for loop like the one below can be used to do that. It loops through a string called s, printing the string, character by character, each on a separate line:
for i in range(len(s)):
print (s[i])
In the range statement we have len(s) that returns how long s is. So, if s were 5 characters long, this would be like having range(5) and the loop variable i would run from 0 to 4. This means that s[i] will run through the characters of s. This way of looping is useful if we need to keep track of our location in the string during the loop.
If we don't need to keep track of our location, then there is a simpler type of loop we can use:
for c in s:
print(c)
This loop will step through s, character by character, with c holding the current character. You can almost read this like an English sentence, “For every character c in s, print that character.”
String methods
Strings come with a ton of methods, functions that return information about the string or return a new string that is a modified version of the original. Here are some of the most useful ones:
| Method | Description |
|---|---|
lower() | returns a string with every letter of the original in lowercase |
upper() | returns a string with every letter of the original in uppercase |
replace(x,y) | returns a string with every occurrence of x replaced by y |
count(x) | counts the number of occurrences of x in the string |
index(x) | returns the location of the first occurrence of x |
isalpha() | returns True if every character of the string is a letter |
Important note
One very important note about lower, upper, and replace is that they do not change the original string. If you want to change a string, s, to all lowercase, it is not enough to just use s.lower(). You need to do the following:
s = s.lower()
Short examples
Here are some examples of string methods in action:
| Statement | Description |
|---|---|
print(s.count(' ')) | prints the number of spaces in the string |
s = s.upper() | changes the string to all caps |
s = s.replace('Hi', 'Hello') | replaces each 'Hi' in s with 'Hello' |
print(s.index('a')) | prints location of the first 'a' in s |
isalpha
The isalpha method is used to tell if a character is a letter or not. It returns True if the character is a letter and False otherwise. When used with an entire string, it will only return True if every character of the string is a letter. The values True and False are called booleans and are covered in this section. For now, though, just remember that you can use isalpha in if conditions. Here is a simple example:
s = input('Enter a string')
if s[0].isalpha():
print('Your string starts with a letter')
if not s.isalpha():
print('Your string contains a non-letter.')
A note about index
If you try to find the index of something that is not in a string, Python will raise an error. For instance, if s='abc' and you try s.index('z'), you will get an error. One way around this is to check first, like below:
if 'z' in s:
location = s.index('z')
Other string methods
There are many more string methods. For instance, there are methods isdigit and isalnum, which are analogous to isalpha. Some other useful methods we will learn about later are join and split. To see a list of all the string methods, type dir(str) into the Python shell. If you do this, you will see a bunch of names that start with __. You can ignore them. To read Python's documentation for one of the methods, say the isdigit method, type help(str.isdigit).
Escape characters
The backslash, \, is used to get certain special characters, called escape characters, into your string. There are a variety of escape characters, and here are the most useful ones:
-
\nthe newline character. It is used to advance to the next line. Here is an example:print('Hi\n\nthere!')Hi There!
-
\'for inserting apostrophes into strings. Say you have the following string:s = 'I can't go'
This will produce an error because the apostrophe will actually end the string. You can use
\'to get around this:s = 'I can\'t go'
Another option is to use double quotes for the string:
"s = I can't go"
-
\"analogous to\'. -
\\This is used to get the backslash itself. For example:filename = 'c:\\programs\\file.py'
-
\tthe tab character
Examples
Example 1
An easy way to print a blank line is print(). However, if we want to print ten blank lines, a quick way to do that is the following:
print('\n'*9)
Note that we get one of the ten lines from the print function itself.
Example 2
Write a program that asks the user for a string and prints out the location of each 'a' in the string.
s = input('Enter some text: ')
for i in range(len(s)):
if s[i]=='a':
print(i)
We use a loop to scan through the string one character at a time. The loop variable i keeps track of our location in the string, and s[i] gives the character at that location. Thus, the third line checks each character to see if it is an 'a', and if so, it will print out i, the location of that 'a'.
Example 3
Write a program that asks the user for a string and creates a new string that doubles each character of the original string. For instance, if the user enters Hello, the output should be HHeelllloo.
s = input('Enter some text: ')
doubled_s = '';
for c in s:
doubled_s = doubled_s + c*2
Here we can use the second type of loop from this section. The variable c will run through the characters of s. We use the repetition operator, *, to double each character. We build up the string s in the way described at the end of this section.
Example 4
Write a program that asks a user for their name and prints it in the following funny pattern:
E El Elv Elvi Elvis
We will require a loop because we have to repeatedly print sections of the string, and to print the sections of the string, we will use a slice:
name = input('Enter your name: ')
for i in range(len(name)):
print(name[:i+1], end=' ')
The one trick is to use the loop variable i in the slice. Since the number of characters we need to print is changing, we need a variable amount in the slice. This is reminiscent of the triangle program from this section. We want to print one character of the name the first time through the loop, two characters the second time, etc. The loop variable, i, starts at 0 the first time through the loop, then increases to 1 the second time through the loop, etc. Thus we use name[:i+1] to print the first i+1 characters of the name. Finally, to get all the slices to print on the same line, we use the print function's optional argument end=' '.
Example 5
Write a program that removes all capitalization and common punctuation from a string s.
s = s.lower()
for c in ',.;:-?!()\'"':
s = s.replace(c, '';)
The way this works is for every character in the string of punctuation, we replace every occurrence of it in s with the empty string, '';. One technical note here: We need the ' character in a string. As described in the previous section, we get it into the string by using the escape character \'.
Example 6
Write a program that, given a string that contains a decimal number, prints out the decimal part of the number. For instance, if given 3.14159, the program should print out .14159.
s = input('Enter your decimal number: ')
print(s[s.index('.')+1:])
The key here is the index method will find where the decimal point is. The decimal part of the number starts there and runs to the end of the string, so we use a slice that starts at s.index('.').
Here is another, more mathematical way, to do this:
from math import floor
num = eval(input('Enter your decimal number: ')
print(num - floor(num))
One difference between the two methods is the first produces a string, whereas the second produces a number.
Example 7
A simple and very old method of sending secret messages is the substitution cipher. Basically, each letter of the alphabet gets replaced by another letter of the alphabet, say every a gets replaced with an x, and every b gets replaced by a z, etc. Write a program to implement this.
alphabet = 'abcdefghijklmnopqrstuvwxyz'
key = 'xznlwebgjhqdyvtkfuompciasr'
secret_message = input('Enter your message: ')
secret_message = secret_message.lower()
for c in secret_message:
if c.isalpha():
print(key[alphabet.index(c)],end='';)
else:
print(c, end='';)
The string key is a random reordering of the alphabet.
The only tricky part of the program is the for loop. What it does is go through the message one character at a time, and, for every letter it finds, it replaces it with the corresponding letter from the key. This is accomplished by using the index method to find the position in the alphabet of the current letter and replacing that letter with the letter from the key at that position. All non-letter characters are copied as is. The program uses the isalpha method to tell whether the current character is a letter or not.
The code to decipher a message is nearly the same. Just change key[alphabet.index(c)] to alphabet[key.index(c)]. This section provides a different approach to the substitution cipher.
Exercises
- Write a program that asks the user to enter a string. The program should then print the following:
- The total number of characters in the string
- The string repeated 10 times
- The first character of the string (remember that string indices start at 0)
- The first three characters of the string
- The last three characters of the string
- The string backwards
- The seventh character of the string if the string is long enough and a message otherwise
- The string with its first and last characters removed
- The string in all caps
- The string with every a replaced with an e
- The string with every letter replaced by a space
- A simple way to estimate the number of words in a string is to count the number of spaces in the string. Write a program that asks the user for a string and returns an estimate of how many words are in the string.
- People often forget closing parentheses when entering formulas. Write a program that asks the user to enter a formula and prints out whether the formula has the same number of opening and closing parentheses.
- Write a program that asks the user to enter a word and prints out whether that word contains any vowels.
- Write a program that asks the user to enter a string. The program should create a new string called
new_stringfrom the user's string such that the second character is changed to an asterisk and three exclamation points are attached to the end of the string. Finally, printnew_string. Typical output is shown below:Enter your string: Qbert Q*ert!!!
- Write a program that asks the user to enter a string
sand then convertssto lowercase, removes all the periods and commas froms, and prints the resulting string. - Write a program that asks the user to enter a word and determines whether the word is a palindrome or not. A palindrome is a word that reads the same backwards as forwards.
- At a certain school, student email addresses end with
@student.college.edu, while professor email addresses end with@prof.college.edu. Write a program that first asks the user how many email addresses they will be entering, and then has the user enter those addresses. After all the email addresses are entered, the program should print out a message indicating either that all the addresses are student addresses or that there were some professor addresses entered. - Ask the user for a number and then print the following, where the pattern ends at the number that the user enters.
1 2 3 4
- Write a program that asks the user to enter a string, then prints out each letter of the string doubled and on a separate line. For instance, if the user entered
HEY, the output would beHH EE YY
- Write a program that asks the user to enter a word that contains the letter a. The program should then print the following two lines: On the first line should be the part of the string up to and including the first a, and on the second line should be the rest of the string. Sample output is shown below:
Enter a word: buffalo buffa lo
- Write a program that asks the user to enter a word and then capitalizes every other letter of that word. So if the user enters
rhinoceros, the program should printrHiNoCeRoS. - Write a program that asks the user to enter two strings of the same length. The program should then check to see if the strings are of the same length. If they are not, the program should print an appropriate message and exit. If they are of the same length, the program should alternate the characters of the two strings. For example, if the user enters
abcdeandABCDEthe program should print outAaBbCcDdEe. - Write a program that asks the user to enter their name in lowercase and then capitalizes the first letter of each word of their name.
- When I was a kid, we used to play this game called Mad Libs. The way it worked was a friend would ask me for some words and then insert those words into a story at specific places and read the story. The story would often turn out to be pretty funny with the words I had given since I had no idea what the story was about. The words were usually from a specific category, like a place, an animal, etc.
For this problem you will write a Mad Libs program. First, you should make up a story and leave out some words of the story. Your program should ask the user to enter some words and tell them what types of words to enter. Then print the full story along with the inserted words. Here is a small example, but you should use your own (longer) example:
Enter a college class: CALCULUS Enter an adjective: HAPPY Enter an activity: PLAY BASKETBALL CALCULUS class was really HAPPY today. We learned how to PLAY BASKETBALL today in class. I can't wait for tomorrow's class!
- Companies often try to personalize their offers to make them more attractive. One simple way to do this is just to insert the person's name at various places in the offer. Of course, companies don't manually type in every person's name; everything is computer-generated. Write a program that asks the user for their name and then generates an offer like the one below. For simplicity's sake, you may assume that the person's first and last names are one word each.
Enter name: George Washington Dear George Washington, I am pleased to offer you our new Platinum Plus Rewards card at a special introductory APR of 47.99%. George, an offer like this does not come along every day, so I urge you to call now toll-free at 1-800-314-1592. We cannot offer such a low rate for long, George, so call right away.
- Write a program that generates the 26-line block of letters partially shown below. Use a loop containing one or two print statements.
abcdefghijklmnopqrstuvwxyz bcdefghijklmnopqrstuvwxyza cdefghijklmnopqrstuvwxyzab ... yzabcdefghijklmnopqrstuvwx zabcdefghijklmnopqrstuvwxy
- The goal of this exercise is to see if you can mimic the behavior of the
inoperator and thecountandindexmethods using only variables, for loops, and if statements.- Without using the
inoperator, write a program that asks the user for a string and a letter and prints out whether or not the letter appears in the string. - Without using the
countmethod, write a program that asks the user for a string and a letter and counts how many occurrences there are of the letter in the string. - Without using the
indexmethod, write a program that asks the user for a string and a letter and prints out the index of the first occurrence of the letter in the string. If the letter is not in the string, the program should say so.
- Without using the
- Write a program that asks the user for a large integer and inserts commas into it according to the standard American convention for commas in large numbers. For instance, if the user enters
1000000, the output should be1,000,000. - Write a program that converts a time from one time zone to another. The user enters the time in the usual American way, such as
3:48pmor11:26am. The first time zone the user enters is that of the original time and the second is the desired time zone. The possible time zones areEastern,Central,Mountain, orPacific.Time: 11:48pm Starting zone: Pacific Ending zone: Eastern 2:48am
- An anagram of a word is a word that is created by rearranging the letters of the original. For instance, two anagrams of idle are deli and lied. Finding anagrams that are real words is beyond our reach until the chapter on text files. Instead, write a program that asks the user for a string and returns a random anagram of the string—in other words, a random rearrangement of the letters of that string.
- A simple way of encrypting a message is to rearrange its characters. One way to rearrange the characters is to pick out the characters at even indices, put them first in the encrypted string, and follow them by the odd characters. For example, the string message would be encrypted as msaeesg because the even characters are m, s, a, e (at indices 0, 2, 4, and 6) and the odd characters are e, s, g (at indices 1, 3, and 5).
- Write a program that asks the user for a string and uses this method to encrypt the string.
- Write a program that decrypts a string that was encrypted with this method.
- A more general version of the above technique is the rail fence cipher, where instead of breaking things into evens and odds, they are broken up by threes, fours or something larger. For instance, in the case of threes, the string secret message would be broken into three groups. The first group is sr sg, the characters at indices 0, 3, 6, 9 and 12. The second group is eemse, the characters at indices 1, 4, 7, 10, and 13. The last group is ctea, the characters at indices 2, 5, 8, and 11. The encrypted message is sr sgeemsectea.
- Write a program the asks the user for a string and uses the rail fence cipher in the threes case to encrypt the string.
- Write a decryption program for the threes case.
- Write a program that asks the user for a string, and an integer determining whether to break things up by threes, fours, or whatever. Encrypt the string using the rail-fence cipher.
- Write a decryption program for the general case.
- In calculus, the derivative of x4 is 4x3. The derivative of x5 is 5x4. The derivative of x6 is 6x5. This pattern continues. Write a program that asks the user for input like
x3orx25and prints the derivative. For example, if the user entersx3, the program should print out3x2. - In algebraic expressions, the symbol for multiplication is often left out, as in 3x+4y or 3(x+5). Computers prefer those expressions to include the multiplication symbol, like
3*x+4*yor3*(x+5). Write a program that asks the user for an algebraic expression and then inserts multiplication symbols where appropriate.
Lists
Say we need to get thirty test scores from a user and do something with them, like put them in order. We could create thirty variables, score1, score2, …, score30, but that would be very tedious. To then put the scores in order would be extremely difficult. The solution is to use lists.
Basics
Creating lists
Here is a simple list:
L = [1,2,3]
Use square brackets to indicate the start and end of the list, and separate the items by commas.
The empty list
The empty list is []. It is the list equivalent of 0 or '';.
Long lists
If you have a long list to enter, you can split it across several lines, like below:
nums = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36, 37, 38, 39, 40]
Input
We can use eval(input()) to allow the user to enter a list. Here is an example:
L = eval(input('Enter a list: '))
print('The first element is ', L[0])
Enter a list: [5,7,9] The first element is 5
Printing lists
You can use the print function to print the entire contents of a list.
L = [1,2,3] print(L)
[1, 2, 3]
Data types
Lists can contain all kinds of things, even other lists. For example, the following is a valid list:
[1, 2.718, 'abc', [5,6,7]]
Similarities to strings
There are a number of things which work the same way for lists as for strings.
-
len— The number of items inLis given bylen(L). -
in— Theinoperator tells you if a list contains something. Here are some examples:if 2 in L: print('Your list contains the number 2.') if 0 not in L: print('Your list has no zeroes.') - Indexing and slicing — These work exactly as with strings. For example,
L[0]is the first item of the listLandL[:3]gives the first three items. -
indexandcount— These methods work the same as they do for strings.%:L.index(x)returns the first location ofxinL(and -1 ifxis not inL), andL.count(x)returns how many timesxappears inL. -
+and*— The+operator adds one list to the end of another. The*operator repeats a list. Here are some examples:Expression Result [7,8] + [3,4,5][7,8,3,4,5][7,8]*3[7,8,7,8,7,8][0]*5[0,0,0,0,0]The last example is particularly useful for quickly creating a list of zeroes.
- Looping — The same two types of loops that work for strings also work for lists. Both of the following examples print out the items of a list, one-by-one, on separate lines.
for i in range(len(L)): for item in L: print(L[i]) print(item)The left loop is useful for problems where you need to use the loop variable
ito keep track of where you are in the loop. If that is not needed, then use the right loop, as it is a little simpler.
Built-in functions
There are several built-in functions that operate on lists. Here are some useful ones:
| Function | Description |
|---|---|
len | returns the number of items in the list |
sum | returns the sum of the items in the list |
min | returns the minimum of the items in the list |
max | returns the maximum of the items in the list |
For example, the following computes the average of the values in a list L:
average = sum(L)/len(L)
List methods
Here are some list methods:
| Method | Description |
|---|---|
append(x) | adds x to the end of the list |
sort() | sorts the list |
count(x) | returns the number of times x occurs in the list |
index(x) | returns the location of the first occurrence of x |
reverse() | reverses the list |
remove(x) | removes first occurrence of x from the list |
pop(p) | removes the item at index p and returns its value |
insert(p,x) | inserts x at index p of the list |
Important note
There is a big difference between list methods and string methods: String methods do not change the original string, but list methods do change the original list. To sort a list L, just use L.sort() and not L=L.sort(). In fact, the latter will not work at all.
| wrong | right |
|---|---|
s.replace('X', 'x') | s = s.replace('X', 'x') |
L = L.sort() | L.sort() |
Other list methods
There are a few others list methods. Type help(list) in the Python shell to see some documentation for them.
Miscellaneous
Making copies of lists
Making copies of lists is a little tricky due to the way Python handles lists. Say we have a list L and we want to make a copy of the list and call it M. The expression M=L will not work for reasons covered in this section. For now, do the following in place of M=L:
M = L[:]
Changing lists
Changing a specific item in a list is easier than with strings. To change the value in location 2 of L to 100, we simply say L[2]=100. If we want to insert the value 100 into location 2 without overwriting what is currently there, we can use the insert method. To delete an entry from a list, we can use the del operator. Some examples are shown below. Assume L=[6,7,8] for each operation.
| Operation | New L | Description |
|---|---|---|
L[1] = 9 | [6, 9, 8] | replace item at index 1 with 9 |
L.insert(1, 9) | [6, 9, 7, 8] | insert a 9 at index 1 without replacing |
del L[1] | [6, 8] | delete second item |
del L[:2] | [8] | delete first two items |
Examples
Example 1
Write a program that generates a list L of 50 random numbers between 1 and 100.
from random import randint
L = []
for i in range(50):
L.append(randint(1,100))
We use the append method to build up the list one item at a time starting with the empty list, []. An alternative to append is to use the following:
L = L + [randint(1,100)]
Example 2
Replace each element in a list L with its square.
for i in range(len(L)):
L[i] = L[i]**2
Example 3
Count how many items in a list L are greater than 50.
count = 0
for item in L:
if item>50:
count=count+1
Example 4
Given a list L that contains numbers between 1 and 100, create a new list whose first element is how many ones are in L, whose second element is how many twos are in L, etc.
frequencies = []
for i in range(1,101):
frequences.append(L.count(i))
The key is the list method count that tells how many times a something occurs in a list.
Example 5
Write a program that prints out the two largest and two smallest elements of a list called scores.
scores.sort()
print('Two smallest: ', scores[0], scores[1])
print('Two largest: ', scores[-1], scores[-2])
Once we sort the list, the smallest values are at the beginning and the largest are at the end.
Example 6
Here is a program to play a simple quiz game.
num_right = 0
# Question 1
print('What is the capital of France?', end=' ')
guess = input()
if guess.lower()=='paris':
print('Correct!')
num_right+=1
else:
print('Wrong. The answer is Paris.')
print('You have', num_right, 'out of 1 right')
#Question 2
print('Which state has only one neighbor?', end=' ')
guess = input()
if guess.lower()=='maine':
print('Correct!')
num_right+=1
else:
print('Wrong. The answer is Maine.')
print('You have', num_right, 'out of 2 right,')
The code works, but it is very tedious. If we want to add more questions, we have to copy and paste one of these blocks of code and then change a bunch of things. If we decide to change one of the questions or the order of the questions, then there is a fair amount of rewriting involved. If we decide to change the design of the game, like not telling the user the correct answer, then every single block of code has to be rewritten. Tedious code like this can often be greatly simplified with lists and loops:
questions = ['What is the capital of France?',
'Which state has only one neighbor?']
answers = ['Paris','Maine']
num_right = 0
for i in range(len(questions)):
guess = input(questions[i])
if guess.lower()==answers[i].lower():
print('Correct')
num_right=num_right+1
else:
print('Wrong. The answer is', answers[i])
print('You have', num_right, 'out of', i+1, 'right.')
If you look carefully at this code, you will see that the code in the loop is the nearly the same as the code of one of the blocks in the previous program, except that in the statements where we print the questions and answers, we use questions[i] and answers[i] in place of the actual text of the questions themselves.
This illustrates the general technique: If you find yourself repeating the same code over and over, try lists and a for loop. The few parts of your repetitious code that are varying are where the list code will go.
The benefits of this are that to change a question, add a question, or change the order, only the questions and answers lists need to be changed. Also, if you want to make a change to the program, like not telling the user the correct answer, then all you have to do is modify a single line, instead of twenty copies of that line spread throughout the program.
Exercises
- Write a program that asks the user to enter a list of integers. Do the following:
- Print the total number of items in the list.
- Print the last item in the list.
- Print the list in reverse order.
- Print
Yesif the list contains a 5 andNootherwise. - Print the number of fives in the list.
- Remove the first and last items from the list, sort the remaining items, and print the result.
- Print how many integers in the list are less than 5.
- Write a program that generates a list of 20 random numbers between 1 and 100.
- Print the list.
- Print the average of the elements in the list.
- Print the largest and smallest values in the list.
- Print the second largest and second smallest entries in the list
- Print how many even numbers are in the list.
- Start with the list
[8,9,10]. Do the following:- Set the second entry (index 1) to 17
- Add 4, 5, and 6 to the end of the list
- Remove the first entry from the list
- Sort the list
- Double the list
- Insert 25 at index 3
The final list should equal
[4,5,6,25,10,17,4,5,6,10,17] - Ask the user to enter a list containing numbers between 1 and 12. Then replace all of the entries in the list that are greater than 10 with 10.
- Ask the user to enter a list of strings. Create a new list that consists of those strings with their first characters removed.
- Create the following lists using a for loop.
- A list consisting of the integers 0 through 49
- A list containing the squares of the integers 1 through 50.
- The list
['a', 'bb', 'ccc', 'dddd',…]that ends with 26 copies of the letter z.
- Write a program that takes any two lists
LandMof the same size and adds their elements together to form a new listNwhose elements are sums of the corresponding elements inLandM. For instance, ifL=[3,1,4]andM=[1,5,9], thenNshould equal[4,6,13]. - Write a program that asks the user for an integer and creates a list that consists of the factors of that integer.
-
When playing games where you have to roll two dice, it is nice to know the odds of each roll. For instance, the odds of rolling a 12 are about 3%, and the odds of rolling a 7 are about 17%. You can compute these mathematically, but if you don't know the math, you can write a program to do it. To do this, your program should simulate rolling two dice about 10,000 times and compute and print out the percentage of rolls that come out to be 2, 3, 4, …, 12.
- Write a program that rotates the elements of a list so that the element at the first index moves to the second index, the element in the second index moves to the third index, etc., and the element in the last index moves to the first index.
- Using a for loop, create the list below, which consists of ones separated by increasingly many zeroes. The last two ones in the list should be separated by ten zeroes.
[1,1,0,1,0,0,1,0,0,0,1,0,0,0,0,1,....] - Write a program that generates 100 random integers that are either 0 or 1. Then find the longest run of zeros, the largest number of zeros in a row. For instance, the longest run of zeros in
[1,0,1,1,0,0,0,0,1,0,0]is 4. - Write a program that removes any repeated items from a list so that each item appears at most once. For instance, the list
[1,1,2,3,4,3,0,0]would become[1,2,3,4,0]. - Write a program that asks the user to enter a length in feet. The program should then give the user the option to convert from feet into inches, yards, miles, millimeters, centimeters, meters, or kilometers. Say if the user enters a
1, then the program converts to inches, if they enter a2, then the program converts to yards, etc. While this can be done with if statements, it is much shorter with lists and it is also easier to add new conversions if you use lists. - There is a provably unbreakable cipher called a one-time pad. The way it works is you shift each character of the message by a random amount between 1 and 26 characters, wrapping around the alphabet if necessary. For instance, if the current character is y and the shift is 5, then the new character is d. Each character gets its own shift, so there needs to be as many random shifts as there are characters in the message. As an example, suppose the user enters secret. The program should generate a random shift between 1 and 26 for each character. Suppose the randomly generated shifts are 1, 3, 2, 10, 8, and 2. The encrypted message would be thebmv.
- Write a program that asks the user for a message and encrypts the message using the one-time pad. First convert the string to lowercase. Any spaces and punctuation in the string should be left unchanged. For example,
Secret!!!becomesthebmv!!!using the shifts above. - Write a program to decrypt a string encrypted as above.
The reason it is called a one-time-pad is that the list of random shifts should only be used once. It becomes easily breakable if the same random shifts are used for more than one message. Moreover, it is only provably unbreakable if the random numbers are truly random, and the numbers generated by
randintare not truly random. For this problem, just userandint, but for cryptographically safe random numbers, see this section. - Write a program that asks the user for a message and encrypts the message using the one-time pad. First convert the string to lowercase. Any spaces and punctuation in the string should be left unchanged. For example,
More with Lists
Lists and the random module
There are some nice functions in the random module that work on lists.
| Function | Description |
|---|---|
choice(L) | picks a random item from L |
sample(L,n) | picks a group of n random items from L |
shuffle(L) | Shuffles the items of L |
Note
Theshuffle function modifies the original list, so if you don't want your list changed, you'll need to make a copy of it.
Example 1
We can use choice to pick a name from a list of names.
from random import choice names = ['Joe', 'Bob', 'Sue', 'Sally'] current_player = choice(names)
Example 2
The sample function is similar to choice. Whereas choice picks one item from a list, sample can be used to pick several.
from random import sample names = ['Joe', 'Bob', 'Sue', 'Sally'] team = sample(names, 2)
Example 3
The choice function also works with strings, picking a random character from a string. Here is an example that uses choice to fill the screen with a bunch of random characters.
from random import choice
s='abcdefghijklmnopqrstuvwxyz1234567890!@#$%^&*()'
for i in range(10000):
print(choice(s), end='';)
Example 4
Here is a nice use of shuffle to pick a random ordering of players in a game.
from random import shuffle
players = ['Joe', 'Bob', 'Sue', 'Sally']
shuffle(players)
for p in players:
print(p, 'it is your turn.')
# code to play the game goes here...
Example 5
Here we use shuffle divide a group of people into teams of two. Assume we are given a list called names.
shuffle(names)
teams = []
for i in range(0,len(names),2):
teams.append([names[i], names[i+1]])
Each item in teams is a list of two names. The way the code works is we shuffle the names so they are in a random order. The first two names in the shuffled list become the first team, the next two names become the second team, etc. Notice that we use the optional third argument to range to skip ahead by two through the list of names.
split
The split method returns a list of the words of a string. The method assumes that words are separated by whitespace, which can be either spaces, tabs or newline characters. Here is an example:
s = 'Hi! This is a test.' print(s.split())
['Hi!', 'This', 'is', 'a', 'test.']
As we can see, since split breaks up the string at spaces, the punctuation will be part of the words. There is a module called string that contains, among other things, a string variable called punctuation that contains common punctuation. We can remove the punctuation from a string s with the following code:
from string import punctuation
for c in punctuation:
s = s.replace(c, '';)
Example
Here is a program that counts how many times a certain word occurs in a string.
from string import punctuation
s = input('Enter a string: ')
for c in punctuation:
s = s.replace(c, '';)
s = s.lower()
L = s.split()
word = input('Enter a word: ')
print(word, 'appears', L.count(word), 'times.')
Optional argument
The split method takes an optional argument that allows it to break the string at places other than spaces. Here is an example:
s = '1-800-271-8281'
print(s.split('-'))
['1', '800', '271', '8281']
join
The join method is in some sense the opposite of split. It is a string method that takes a list of strings and joins them together into a single string. Here are some examples, using the list L = ['A', 'B', 'C']
| Operation | Result |
|---|---|
' '.join(L) | A B C |
'';.join(L) | ABC |
', '.join(L) | A, B, C |
'***'.join(L) | A***B***C |
Example
Write a program that creates an anagram of a given word. An anagram of a word uses the same letters as the word but in a different order. For instance, two anagrams of the word there are three and ether. Don't worry about whether the anagram is a real word or not.
This sounds like something we could use shuffle for, but shuffle only works with lists. What we need to do is convert our string into a list, use shuffle on it, and then convert the list back into a string. To turn a string s into a list, we can use list(s). (See this section.) To turn the list back into a string, we will use join.
from random import shuffle
word = input('Enter a word: ')
letter_list = list(word)
shuffle(letter_list)
anagram = '';.join(letter_list)
print(anagram)
List comprehensions
List comprehensions are a powerful way to create lists. Here is a simple example:
L = [i for i in range(5)]
This creates the list [0,1,2,3,4]. Notice that the syntax of a list comprehension is somewhat reminiscent of set notation in mathematics. Here are a couple more examples of list comprehensions. For these examples, assume the following:
string = 'Hello' L = [1,14,5,9,12] M = ['one', 'two', 'three', 'four', 'five', 'six']
| List comprehension | Resulting list |
|---|---|
[0 for i in range(10)] | [0,0,0,0,0,0,0,0,0,0] |
[i**2 for i in range(1,8)] | [1,4,9,16,25,36,49] |
[i*10 for i in L] | [10,140,50,90,120] |
[c*2 for c in string] | ['HH', 'ee', 'll', 'll', 'oo'] |
[m[0] for m in M] | ['o', 't', 't', 'f', 'f', 's'] |
[i for i in L if i<10] | [1,5,9] |
[m[0] for m in M if len(m)==3] | ['o', 't', 's'] |
As we see in the last two examples, we can add an if to a list comprehension. Compare the last example with the long way of building the list:
L = []
for m in M:
if len(m)==3:
L.append(m)
Multiple fors
You can use more than one for in a list comprehension:
L = [[i,j] for i in range(2) for j in range(2)]
[[0, 0], [0, 1], [1, 0], [1, 1]]
This is the equivalent of the following code:
L = []
for i in range(2):
for j in range(2):
L.append([i,j])
Here is another example:
[[i,j] for i in range(4) for j in range(i)]
[[1, 0], [2, 0], [2, 1], [3, 0], [3, 1], [3, 2]]
Using list comprehensions
To further demonstrate the power of list comprehensions, we will do the first four examples of this section in one line apiece using list comprehensions.
Example 1
Write a program that generates a list L of 50 random numbers between 1 and 100.
L = [randint(1,100) for i in range(50)]
Example 2
Replace each element in a list L with its square.
L = [i**2 for i in L]
Example 3
Count how many items in a list L are greater than 50.
len([i for i in L if i>50])
Example 4
Given a list L that contains numbers between 1 and 100, create a new list whose first element is how many ones are in L, whose second element is how many twos are in L, etc.
frequencies = [L.count(i) for i in range(1,101)]
Another example
The join method can often be used with list comprehensions to quickly build up a string. Here we create a string that contains a random assortment of 1000 letters.
from random import choice alphabet = 'abcdefghijklmnopqrstuvwxyz' s = '';.join([choice(alphabet) for i in range(1000)])
One more example
Suppose we have a list whose elements are lists of size 2, like below:
L = [[1,2], [3,4], [5,6]]
If we want to flip the order of the entries in the lists, we can use the following list comprehension:
M = [[y,x] for x,y in L]
[[2, 1], [4, 3], [6, 5]]
Note
You can certainly get away without using list comprehensions, but once you get the hang of them, you'll find they are both quicker to write and easier to read than the longer ways of creating lists.Two-dimensional lists
There are a number of common things that can be represented by two-dimensional lists, like a Tic-tac-toe board or the pixels on a computer screen. In Python, one way to create a two-dimensional list is to create a list whose items are themselves lists. Here is an example:
L = [[1,2,3],
[4,5,6],
[7,8,9]]
Indexing
We use two indices to access individual items. To get the entry in row r, column c, use the following:
L[r][c]
Printing a two-dimensional list
To print a two-dimensional list, you can use nested for loops. The following example prints a 10 × 5 list:
for r in range(10):
for c in range(5):
print(L[r][c], end=" ")
print()
Another option is to use the pprint function of the pprint module. This function is used to “pretty-print” its argument. Here is an example to print a list L:
from pprint import pprint pprint(L)
The pprint function can be used to nicely print ordinary lists and other objects in Python.
Working with two-dimensional lists
Nested for loops, like the ones used in printing a two-dimensional list, can also be used to process the items in a two-dimensional list. Here is an example that counts how many entries in a 10 × 5 list are even.
count = 0
for r in range(10):
for c in range(5):
if L[r][c]%2==0:
count = count + 1
This can also be done with a list comprehension:
count = sum([1 for r in range(10) for c in range(5) if L[r][c]%2==0])
Creating large two-dimensional lists
To create a larger list, you can use a list comprehension like below:
L = [[0]*50 for i in range(100)]
This creates a list of zeroes with 100 rows and 50 columns.
Picking out rows and columns
To get the row r of L (starting at row r=0), use the following:
L[r]
To get column c of L (starting at column c=0), use a list comprehension:
[L[i][c] for i in range(len(L))]
Flattening a list
To flatten a two-dimensional list, that is, return a one-dimensional list of its elements, use the following:
[j for row in L for j in row]
For instance, suppose we have the following list:
L = [[1,2,3],
[4,5,6],
[7,8,9]]
The flattened list will be:
[1, 2, 3, 4, 5, 6, 7, 8, 9]
Higher dimensions
Creating and using 3-dimensional and higher lists is similar. Here we create a 5 × 5× 5 list:
L = [[[0]*5 for i in range(5)] for j in range(5)]
It is a list whose items are lists of lists. The first entry in the list is
L[0][0][0]
Exercises
- Write a program that asks the user to enter some text and then counts how many articles are in the text. Articles are the words
'a','an', and'the'. - Write a program that allows the user to enter five numbers (read as strings). Create a string that consists of the user's numbers separated by plus signs. For instance, if the user enters 2, 5, 11, 33, and 55, then the string should be
'2+5+11+33+55'. -
- Ask the user to enter a sentence and print out the third word of the sentence.
- Ask the user to enter a sentence and print out every third word of the sentence.
-
- Write a program that asks the user to enter a sentence and then randomly rearranges the words of the sentence. Don't worry about getting punctuation or capitalization correct.
- Do the above problem, but now make sure that the sentence starts with a capital, that the original first word is not capitalized if it comes in the middle of the sentence, and that the period is in the right place.
- Write a simple quote-of-the-day program. The program should contain a list of quotes, and when the user runs the program, a randomly selected quote should be printed.
- Write a simple lottery drawing program. The lottery drawing should consist of six different numbers between 1 and 48.
- Write a program that estimates the average number of drawings it takes before the user's numbers are picked in a lottery that consists of correctly picking six different numbers that are between 1 and 10. To do this, run a loop 1000 times that randomly generates a set of user numbers and simulates drawings until the user's numbers are drawn. Find the average number of drawings needed over the 1000 times the loop runs.
- Write a program that simulates drawing names out of a hat. In this drawing, the number of hat entries each person gets may vary. Allow the user to input a list of names and a list of how many entries each person has in the drawing, and print out who wins the drawing.
- Write a simple quiz game that has a list of ten questions and a list of answers to those questions. The game should give the player four randomly selected questions to answer. It should ask the questions one-by-one, and tell the player whether they got the question right or wrong. At the end it should print out how many out of four they got right.
- Write a censoring program. Allow the user to enter some text and your program should print out the text with all the curse words starred out. The number of stars should match the length of the curse word. For the purposes of this program, just use the“curse” words darn, dang, freakin, heck, and shoot. Sample output is below:
Enter some text: Oh shoot, I thought I had the dang problem figured out. Darn it. Oh well, it was a heck of a freakin try. Oh *****, I thought I had the **** problem figured out. **** it. Oh well, it was a **** of a ****** try.
- This section described how to use the
shufflemethod to create a random anagram of a string. Use thechoicemethod to create a random anagram of a string. - Write a program that gets a string from the user containing a potential telephone number. The program should print
Validif it decides the phone number is a real phone number, andInvalidotherwise. A phone number is considered valid as long as it is written in the form abc-def-hijk or 1-abc-def-hijk. The dashes must be included, the phone number should contain only numbers and dashes, and the number of digits in each group must be correct. Test your program with the output shown below.Enter a phone number: 1-301-447-5820 Valid Enter a phone number: 301-447-5820 Valid Enter a phone number: 301-4477-5820 Invalid Enter a phone number: 3X1-447-5820 Invalid Enter a phone number: 3014475820 Invalid
- Let
Lbe a list of strings. Write list comprehensions that create new lists fromLfor each of the following.- A list that consists of the strings of
swith their first characters removed - A list of the lengths of the strings of
s - A list that consists of only those strings of
sthat are at least three characters long
- A list that consists of the strings of
- Use a list comprehension to produce a list that consists of all palindromic numbers between 100 and 1000.
- Use a list comprehension to create the list below, which consists of ones separated by increasingly many zeroes. The last two ones in the list should be separated by ten zeroes.
[1,1,0,1,0,0,1,0,0,0,1,0,0,0,0,1,....]
- Let
L=[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47]. Use a list comprehension to produce a list of the gaps between consecutive entries inL. Then find the maximum gap size and the percentage of gaps that have size 2. - Write a program that finds the average of all of the entries in a 4 × 4 list of integers.
- Write a program that creates a 10 × 10 list of random integers between 1 and 100. Then do the following:
- Print the list.
- Find the largest value in the third row.
- Find the smallest value in the sixth column.
- Write a program that creates and prints an 8 × 8 list whose entries alternate between 1 and 2 in a checkerboard pattern, starting with 1 in the upper left corner.
- Write a program that checks to see if a 4 × 4 list is a magic square. In a magic square, every row, column, and the two diagonals add up to the same value.
- Write a program that asks the user to enter a length. The program should ask them what unit the length is in and what unit they would like to convert it to. The possible units are inches, yards, miles, millimeters, centimeters, meters, and kilometers. While this can be done with 25 if statements, it is shorter and easier to add on to if you use a two-dimensional list of conversions, so please use lists for this problem.
- The following is useful as part of a program to play Battleship. Suppose you have a 5 × 5 list that consists of zeroes and ones. Ask the user to enter a row and a column. If the entry in the list at that row and column is a one, the program should print
Hitand otherwise it should printMiss. - This exercise is useful in creating a Memory game. Randomly generate a 6 × 6 list of assorted characters such that there are exactly two of each character. An example is shown below.
@ 5 # A A ! 5 0 b @ $ z $ N x ! N z 0 - + # b : - : + c c x
- The following is useful in implementing computer players in a number of different games. Write a program that creates a 5 × 5 list consisting of zeroes and ones. Your program should then pick a random location in the list that contains a zero and change it to a one. If all the entries are one, the program should say so. [Hint: one way to do this is to create a new list whose items are the coordinates of all the ones in the list and use the
choicemethod to randomly select one. Use a two-element list to represent a set of coordinates.] - Here is an old puzzle question you can solve with a computer program. There is only one five-digit number n that is such that every one of the following ten numbers shares exactly one digit in common in the same position as n. Find n.
01265, 12171, 23257, 34548, 45970, 56236, 67324, 78084, 89872, 99414
- We usually refer to the entries of a two-dimensional list by their row and column, like below on the left. Another way is shown below on the right.
(0,0) (0,1) (0,2) 0 1 2 (1,0) (1,1) (1,2) 3 4 5 (2,0) (2,1) (2,2) 6 7 8
- Write some code that translates from the left representation to the right one. The
//and%operators will be useful. Be sure your code works for arrays of any size. - Write some code that translates from the right representation to the left one.
- Write some code that translates from the left representation to the right one. The
While loops
We have already learned about for loops, which allow us to repeat things a specified number of times. Sometimes, though, we need to repeat something, but we don't know ahead of time exactly how many times it has to be repeated. For instance, a game of Tic-tac-toe keeps going until someone wins or there are no more moves to be made, so the number of turns will vary from game to game. This is a situation that would call for a while loop.
Examples
Example 1
Let's go back to the first program we wrote back in this section, the temperature converter. One annoying thing about it is that the user has to restart the program for every new temperature. A while loop will allow the user to repeatedly enter temperatures. A simple way for the user to indicate that they are done is to have them enter a nonsense temperature like -1000 (which is below absolute 0). This is done below:
temp = 0
while temp!=-1000:
temp = eval(input('Enter a temperature (-1000 to quit): '))
print('In Fahrenheit that is', 9/5*temp+32)
Look at the while statement first. It says that we will keep looping, that is, keep getting and converting temperatures, as long as the temperature entered is not -1000. As soon as -1000 is entered, the while loop stops. Tracing through, the program first compares temp to -1000. If temp is not -1000, then the program asks for a temperature and converts it. The program then loops back up and again compares temp to -1000. If temp is not -1000, the program will ask for another temperature, convert it, and then loop back up again and do another comparison. It continues this process until the user enters -1000.
We need the line temp=0 at the start, as without it, we would get a name error. The program would get to the while statement, try to see if temp is not equal to -1000 and run into a problem because temp doesn't yet exist. To take care of this, we just declare temp equal to 0. There is nothing special about the value 0 here. We could set it to anything except -1000. (Setting it to -1000 would cause the condition on the while loop to be false right from the start and the loop would never run.)
Note that is natural to think of the while loop as continuing looping until the user enters -1000. However, when we construct the condition, instead of thinking about when to stop looping, we instead need to think in terms of what has to be true in order to keep going.
A while loop is a lot like an if statement. The difference is that the indented statements in an if block will only be executed once, whereas the indented statements in a while loop are repeatedly executed.
Example 2
One problem with the previous program is that when the user enters in -1000 to quit, the program still converts the value -1000 and doesn't give any message to indicate that the program has ended. A nicer way to do the program is shown below.
temp = 0
while temp!=-1000:
temp = eval(input('Enter a temperature (-1000 to quit): '))
if temp!=-1000:
print('In Fahrenheit that is', 9/5*temp+32)
else:
print('Bye!')
Example 3
When first met if statements in this section, we wrote a program that played a simple random number guessing game. The problem with that program is that the player only gets one guess. We can, in a sense, replace the if statement in that program with a while loop to create a program that allows the user to keep guessing until they get it right.
from random import randint
secret_num = randint(1,10)
guess = 0
while guess != secret_num:
guess = eval(input('Guess the secret number: '))
print('You finally got it!')
The condition guess != secret_num says that as long as the current guess is not correct, we will keep looping. In this case, the loop consists of one statement, the input statement, and so the program will keep asking the user for a guess until their guess is correct. We require the line guess = 0 prior to the while loop so that the first time the program reaches the loop, there is something in guess for the program to use in the comparison. The exact value of guess doesn't really matter at this point. We just want something that is guaranteed to be different than secret_num. When the user finally guesses the right answer, the loop ends and program control moves to the print statement after the loop, which prints a congratulatory message to the player.
Example 4
We can use a while loop to mimic a for loop, as shown below. Both loops have the exact same effect.
for i in range(10): i=0
print(i) while i<10:
print(i)
i=i+1
Remember that the for loop starts with the loop variable i equal to 0 and ends with it equal to 9. To use a while loop to mimic the for loop, we have to manually create our own loop variable i. We start by setting it to 0. In the while loop we have the same print statement as in the for loop, but we have another statement, i=i+1, to manually increase the loop variable, something that the for loop does automatically.
Example 5
Below is our old friend that converts from Fahrenheit to Celsius.
temp = eval(input('Enter a temperature in Celsius: '))
print('In Fahrenheit, that is', 9/5*temp+32)
A program that gets input from a user may want to check to see that the user has entered valid data. The smallest possible temperature is absolute zero, -273.15°C. The program below takes absolute zero into account:
temp = eval(input('Enter a temperature in Celsius: '))
if temp<-273.15:
print('That temperature is not possible.'))
else:
print('In Fahrenheit, that is', 9/5*temp+32)
One way to improve this is to allow the user to keep reentering the temperature until they enter a valid one. You may have experienced something similar using an online form to enter a phone number or a credit card number. If you enter an invalid number, you are told to reenter it. In the code below, the while loop acts very similarly to the if statement in the previous example.
temp = eval(input('Enter a temperature in Celsius: '))
while temp<-273.15:
temp = eval(input('Impossible. Enter a valid temperature: '))
print('In Fahrenheit, that is', 9/5*temp+32)
Note that we do not need an else statement here, like we had with the if statement.. The condition on the while loop guarantees that we will only get to the print statement once the user enters a valid temperature. Until that point, the program will be stuck in the loop, continually asking the user for a new temperature.
Example 6
As mentioned before, it is a valuable skill is to be able to read code. One way to do so is to pretend to be the Python interpreter and go through the code line by line. Let's try it with the code below.
i = 0
while i<50:
print(i)
i=i+2
print('Bye!')
The variable i gets set to 0 to start. Next, the program tests the condition on the while loop. Because i is 0, which is less than 50, the code indented under the while statement will get executed. This code prints the current value of i and then executes the statement i=i+2 which adds 2 to i.
The variable i is now 2 and the program loops back to the while statement. It checks to see if i is less than 50, and since i is 2, which is less than 50, the indented code should be executed again. So we print i again, add 2 to it, and then loop back to check the while loop condition again. We keep doing this until finally i gets to 50.
At this point, the while condition will finally not be true anymore and the program jumps down to the first statement after the while, which prints Bye!. The end result of the program is the numbers 0, 2, 4, …, 48 followed by the message, Bye!.
Infinite loops
When working with while loops, sooner or later you will accidentally send Python into a never-ending loop. Here is an example:
i=0
while i<10:
print(i)
In this program, the value of i never changes and so the condition i<10 is always true. Python will continuously print zeroes. To stop a program caught in a never-ending loop, use Restart Shell under the Shell menu. You can use this to stop a Python program before it is finished executing.
Sometimes a never-ending loop is what you want. A simple way to create one is shown below:
while True:
# statements to be repeated go here
The value True is called a boolean value and is discussed further in this section.
The break statement
The break statement can be used to break out of a for or while loop before the loop is finished.
Example 1
Here is a program that allows the user to enter up to 10 numbers. The user can stop early by entering a negative number.
for i in range(10):
num = eval(input('Enter number: '))
if num<0:
break
This could also be accomplished with a while loop.
i=0
num=1
while i<10 and num>0:
num = eval(input('Enter a number: '))
Either method is ok. In many cases the break statement can help make your code easier to understand and less clumsy.
Example 2
Earlier in the chapter, we used a while loop to allow the user to repeatedly enter temperatures to be converted. Here is, more or less, the original version on the left compared with a different approach using the break statement.
temp = 0 while True:
while temp!=-1000: temp = eval(input(': '))
temp = eval(input(': ')) if temp==-1000:
if temp!=-1000: print('Bye')
print(9/5*temp+32) break
else: print(9/5*temp+32)
print('Bye!')
The else statement
There is an optional else that you can use with break statements. The code indented under the else gets executed only if the loop completes without a break happening.
Example 1
This is a simple example based off of Example 1 of the previous section.
for i in range(10):
num = eval(input('Enter number: '))
if num<0:
print('Stopped early')
break
else:
print('User entered all ten values')
The program allows the user to enter up to 10 numbers. If they enter a negative, then the program prints Stopped early and asks for no more numbers. If the user enters no negatives, then the program prints User entered all ten values.
Example 2
Here are two ways to check if an integer num is prime. A prime number is a number whose only divisors are 1 and itself. The approach on the left uses a while loop, while the approach on the right uses a for/break loop:
i=2 for i in range(2, num):
while i<num and num%i!=0: if num%i==0:
i=i+1 print('Not prime')
if i==num: break
print('Prime') else:
else: print('Prime')
print('Not prime')
The idea behind both approaches is to scan through all the integers between 2 and num-1, and if any of them is a divisor, then we know num is not prime. To see if a value i is a divisor of num, we just have to check to see if num%i is 0.
The idea of the while loop version is we continue looping as long as we haven't found a divisor. If we get all the way through the loop without finding a divisor, then i will equal num, and in that case the number must be prime.
The idea of the for/break version is we loop through all the potential divisors, and as soon as we find one, we know the number is not prime and we print Not prime and stop looping. If we get all the way through the loop without breaking, then we have not found a divisor. In that case the else block will execute and print that the number is prime.
The guessing game, more nicely done
It is worth going through step-by-step how to develop a program. We will modify the guessing game program from this section to do the following:
- The player only gets five turns.
- The program tells the player after each guess if the number is higher or lower.
- The program prints appropriate messages for when the player wins and loses.
Below is what we want the program to look like:
Enter your guess (1-100): 50 LOWER. 4 guesses left. Enter your guess (1-100): 25 LOWER. 3 guesses left. Enter your guess (1-100): 12 LOWER. 2 guesses left. Enter your guess (1-100): 6 HIGHER. 1 guesses left. Enter your guess (1-100): 9 LOWER. 0 guesses left. You lose. The correct number is 8
First, think about what we will need in the program:
- We need random numbers, so there will be an import statement at the beginning of the program and a
randintfunction somewhere else. - To allow the user to guess until they either guess right or run out of turns, one solution is to use while loop with a condition that takes care of both of these possibilities.
- There will be an input statement to get the user's guess. As this is something that is repeatedly done, it will go inside the loop.
- There will be an if statement to take care of the higher/lower thing. As this comparison will be done repeatedly and will depend on the user's guesses, it will go in the loop after the input statement.
- There will be a counting variable to keep track of how many turns the player has taken. Each time the user makes a guess, the count will go up by one, so this statement will also go inside the loop.
Next start coding those things that are easy to do:
from random import randint
secret_num = randint(1,100)
num_guesses = 0
while #some condition goes here#
guess = eval(input('Enter your guess (1-100): '))
num_guesses = num_guesses + 1
# higher/lower if statement goes here
For the while loop, we want to continue looping as long as the user has not guessed the secret number and as long as the player has not used up all of their guesses:
while guess != secret_num and num_guesses <= 4:
The higher/lower if statement can be done like this:
if guess < secret_num:
print('HIGHER.', 5-num_guesses, 'guesses left.\n')
elif guess > secret_num:
print('LOWER.', 5-num_guesses, 'guesses left.\n')
else:
print('You got it!')
Finally, it would be nice to have a message for the player if they run out of turns. When they run out of turns, the while loop will stop looping and program control will shift to whatever comes outside of the loop. At this point we can print the message, but we only want to do so if the reason that the loop stopped is because of the player running out of turns and not because they guessed correctly. We can accomplish this with an if statement after the loop. This is shown below along with the rest of the completed program.
from random import randint
secret_num = randint(1,100)
num_guesses = 0
guess = 0
while guess != secret_num and num_guesses <= 4:
guess = eval(input('Enter your guess (1-100): '))
num_guesses = num_guesses + 1
if guess < secret_num:
print('HIGHER.', 5-num_guesses, 'guesses left.\n')
elif guess > secret_num:
print('LOWER.', 5-num_guesses, 'guesses left.\n')
else:
print('You got it!')
if num_guesses==5 and guess != secret_num:
print('You lose. The correct number is', secret_num)
Here is an alternative solution using a for/break loop:
from random import randint
secret_num = randint(1,100)
for num_guesses in range(5):
guess = eval(input('Enter your guess (1-100): '))
if guess < secret_num:
print('HIGHER.', 5-num_guesses, 'guesses left.\n')
elif guess > secret_num:
print('LOWER.', 5-num_guesses, 'guesses left.\n')
else:
print('You got it!')
break
else:
print('You lose. The correct number is', secret_num)
Exercises
-
The code below prints the numbers from 1 to 50. Rewrite the code using a while loop to accomplish the same thing.
for i in range(1,51): print(i) -
- Write a program that uses a while loop (not a for loop) to read through a string and print the characters of the string one-by-one on separate lines.
- Modify the program above to print out every second character of the string.
- A good program will make sure that the data its users enter is valid. Write a program that asks the user for a weight and converts it from kilograms to pounds. Whenever the user enters a weight below 0, the program should tell them that their entry is invalid and then ask them again to enter a weight. [Hint: Use a while loop, not an if statement].
- Write a program that asks the user to enter a password. If the user enters the right password, the program should tell them they are logged in to the system. Otherwise, the program should ask them to reenter the password. The user should only get five tries to enter the password, after which point the program should tell them that they are kicked off of the system.
- Write a program that allows the user to enter any number of test scores. The user indicates they are done by entering in a negative number. Print how many of the scores are A's (90 or above). Also print out the average.
- Modify the higher/lower program so that when there is only one guess left, it says
1 guess, not1 guesses. - Recall that, given a string
s,s.index('x')returns the index of the first x insand an error if there is no x.- Write a program that asks the user for a string and a letter. Using a while loop, the program should print the index of the first occurrence of that letter and a message if the string does not contain the letter.
- Write the above program using a for/break loop instead of a while loop.
- The GCD (greatest common divisor) of two numbers is the largest number that both are divisible by. For instance, gcd(18,42) is 6 because the largest number that both 18 and 42 are divisible by is 6. Write a program that asks the user for two numbers and computes their gcd. Shown below is a way to compute the GCD, called Euclid's Algorithm.
- First compute the remainder of dividing the larger number by the smaller number
- Next, replace the larger number with the smaller number and the smaller number with the remainder.
- Repeat this process until the smaller number is 0. The GCD is the last value of the larger number.
- A 4000-year old method to compute the square root of 5 is as follows:
Start with an initial guess, say 1. Then compute
(1+5/1)/2=3.
Next, take that 3 and replace the 1's in the previous formula with 3's . This gives
(3+5/3)/2=7/3 ≈ 2.33.
Next replace the 3 in the previous formula with 7/3. This gives
(7/3+5/(7/3))/2=47/21 ≈ 2.24.
If you keep doing this process of computing the formula, getting a result, and plugging it back in, the values will eventually get closer and closer to √5. This method works for numbers other than 5. Write a program that asks the user for a number and uses this method to estimate the square root of the number correct to within 10-10. The estimate will be correct to within 10-10 when the absolute value of the difference between consecutive values is less than 10-10.
- Write a program that has a list of ten words, some of which have repeated letters and some which don't. Write a program that picks a random word from the list that does not have any repeated letters.
- Write a program that starts with an 5 × 5 list of zeroes and randomly changes exactly ten of those zeroes to ones.
- Write a program in which you have a list that contains seven integers that can be 0 or 1. Find the first nonzero entry in the list and change it to a 1. If there are no nonzero entries, print a message saying so.
- This exercise asked you to write a program that lets the user play Rock-Paper-Scissors against the computer. In that program there were exactly five rounds. Rewrite the program so that it is a best 3 out of 5. That is, the first player to win three times is the winner.
- Write a program to play the following simple game. The player starts with $100. On each turn a coin is flipped and the player has to guess heads or tails. The player wins $9 for each correct guess and loses $10 for each incorrect guess. The game ends either when the player runs out of money or gets to $200.
- Write a program to play the following game. There is a list of several country names and the program randomly picks one. The player then has to guess letters in the word one at a time. Before each guess the country name is displayed with correctly guessed letters filled in and the rest of the letters represented with dashes. For instance, if the country is Canada and the player has correctly guessed a, d, and n, the program would display
-ana-da. The program should continue until the player either guesses all of the letters of the word or gets five letters wrong. - Write a text-based version of the game Memory. The game should generate a 5 × 5 board (see this exercise). Initially the program should display the board as a 5 × 5 grid of asterisks. The user then enters the coordinates of a cell. The program should display the grid with the character at those coordinates now displayed. The user then enters coordinates of another cell. The program should now display the grid with the previous character and the new character displayed. If the two characters match, then they should permanently replace the asterisks in those locations. Otherwise, when the user enters the next set of coordinates, those characters should be replaced by asterisks. The game continues this way until the player matches everything or runs out of turns. You can decide how many turns they player gets.
- Ask the user to enter the numerator and denominator of a fraction, and the digit they want to know. For instance, if the user enters a numerator of 1 and a denominator of 7 and wants to know the 4th digit, your program should print out 8, because 1/7=.142856… and 8 is the 4th digit. One way to do this is to mimic the long division process you may have learned in grade school. It can be done in about five lines using the
//operator at one point in the program. - Randomly generate a 6 × 6 list that has exactly 12 ones placed in random locations in the list. The rest of the entries should be zeroes.
- Randomly generate a 9 × 9 list where the entries are integers between 1 and 9 with no repeat entries in any row or in any column.
Miscellaneous Topics II
In this chapter we will look at variety of useful things to know.
str, int, float, and list
The str, int, float, and list functions are used to convert one data type into another.
str
Quite often we will want to convert a number to a string to take advantage of string methods to break the number apart. The built-in function str is used to convert things into strings. Here are some examples:
| Statement | Result |
|---|---|
str(37) | '37' |
str(3.14) | '3.14' |
str([1,2,3]) | '[1,2,3]' |
int and float
The int function converts something into an integer. The float function converts something into a floating point number. Here are some examples.
| Statement | Result |
|---|---|
int('37') | 37 |
float('3.14') | 3.14 |
int(3.14) | 3 |
To convert a float to an integer, the int function drops everything after the decimal point.
list
The list function takes something that can be converted into a list and makes into a list. Here are two uses of it.
list(range(5)) | [0,1,2,3,4] |
list('abc') | ['a', 'b', 'c'] |
Examples
Example 1
Here is an example that finds all the palindromic numbers between 1 and 10000. A palindromic number is one that is the same backwards as forwards, like 1221 or 64546.
for i in range(1,10001):
s = str(i)
if s==s[::-1]:
print(s)
We use the str function here to turn the integer i into a string so we can use slices to reverse it.
Example 2
Here is an example that tells a person born on January 1, 1991 how old they are in 2010.
birthday = 'January 1, 1991'
year = int(birthday[-4:])
print('You are', 2010-year, 'years old.')
The year is in the last four characters of birthday. We use int to convert those characters into an integer so we can do math with the year.
Example 3
Write a program that takes a number num and adds its digits. For instance, given the number 47, the program should return 11 (which is 4+7). Let us start with a 2-digit example.
digit = str(num) answer = int(digit[0]) + int(digit[1])
The idea here is that we convert num to a string so that we can use indexing to get the two digits separately. We then convert each back to an integer using the int function. Here is a version that handles numbers with arbitrarily many digits:
digit = str(num)
answer = 0
for i in range(len(digit)):
answer = answer + int(digit[i])
We can do the above program in a single line using a list comprehension.
answer = sum([int(c) for c in str(num)])
Example 4
To break a decimal number, num, up into its integer and fractional parts, we can do the following:
ipart = int(num) dpart = num - int(num)
For example, if num is 12.345, then ipart is 12 and dpart is 12.345-12=.345.
Example 5
If we want to check to see if a number is prime, we can do so by checking to see if it has any divisors other than itself and 1. In this section we saw code for this, and we had the following for loop:
for i in range(2,num):
This checks for divisibility by the integers 2, 3, …, num-1. However, it turns out that you really only have to check the integers from 2 to the square root of the number. For instance, to check if 111 is prime, you only need to check if it is divisible by the integers 2 through 10, as √111 ≈ 10.5. We could then try the following for loop:
for i in range(2,num**.5):
However, this gives an error, because num**.5 might not be an integer, and the range function needs integers. We can use int to correct this:
for i in range(2,int(num**.5)+1):
The +1 at the end is needed due to the range function not including the last value.
Booleans
Boolean variables in Python are variables that can take on two values, True and False. Here are two examples of setting Boolean variables:
game_over = True highlight_text = False
Booleans can help make your programs more readable. They are often used as flag variables or to indicate options. Booleans are often used as conditions in if statements and while loops:
if game_over:
print('Bye!')
Note the following equivalences:
if game_over: | ↔ | if game_over==True: |
while not game_over: | ↔ | while game_over==False: |
note
Conditional expressions evaluate to booleans and you can even assign them to variables. For instance, the following assignsTrue to x because 6==6 evaluates to True.
x = (6==6)
We have seen booleans before. The isalpha string method returns True if every character of the string is a letter and False otherwise.
Shortcuts
- Shortcut operators
Operations like
count=count+1occur so often that there is a shorthand for them. Here are a couple of examples:
There are also shortcut operatorsStatement Shorthand count=count+1count+=1total=total-5total-=5prod=prod*2prod*=2/=,%=,//=, and**=. - An assignment shortcut
Look at the code below.
a = 0 b = 0 c = 0
A nice shortcut is:
a = b = c = 0
- Another assignment shortcut
Say we have a list
Lwith three elements in it, and we want to assign those elements to variable names. We could do the following:x = L[0] y = L[1] z = L[2]
Instead, we can do this:
x,y,z = L
Similarly, we can assign three variables at a time like below:
x,y,z = 1,2,3
And, as we have seen once before, we can swap variables using this kind of assignment.
x,y,z = y,z,x
- Shortcuts with conditions
Here are some handy shortcuts:
Statement Shortcut ifa==0andb==0andc==0:ifa==b==c==0:if1<aanda<bandb<5:if1<a<b<5:
Short-circuiting
Say we are writing a program that searches a list of words for those whose fifth character is 'z'. We might try the following:
for w in words:
if w[4]=='z':
print(w)
But with this, we will occasionally get a string index out of range error. The problem is that some words in the list might be less than five characters long. The following if statement, however, will work:
if len(w)>=5 and w[4]=='z':
It might seem like we would still get an error because we are still checking w[4], but there is no error. The key to why this works is short-circuiting. Python starts by checking the first part of the condition, len(w)>=5. If that condition turns out to be false, then the whole and condition is guaranteed to be false, and so there is no point in even looking at the second condition. So Python doesn't bother with the second condition. You can rely on this behavior.
Short-circuiting also happens with or conditions. In this case, Python checks the first part of the or and if it is true, then the whole or is guaranteed to be true, and so Python will not bother checking the second part of the or.
Continuation
Sometimes you'll write a long line of code that would be more readable if it were split across two lines. To do this, use a backslash \ character at the end of the line to indicate that the statement continues onto the next line. Here is an example:
if 'a' in string or 'b' in string or 'c' in string \ or 'd' in string or 'e' in string:
Make sure there are no extra spaces after the backslash or you will get an error message.
If you are entering a list, dictionary, or the arguments of a function, the backslash can be left out:
L = ['Joe', 'Bob', 'Sue', 'Jimmy', 'Todd', 'Frank',
'Mike', 'John', 'Amy', 'Edgar', 'Sam']
pass
The pass statement does nothing. Believe it or not, such a thing does have a few uses that we will see later.
String formatting
Suppose we are writing a program that calculates a 25% tip on a bill of $23.60. When we multiply, we get 5.9, but we would like to display the result as $5.90, not $5.9. Here is how to do it:
a = 23.60 * .25
print('The tip is {:.2f}'.format(a))
This uses the format method of strings. Here is another example:
bill = 23.60
tip = 23.60*.25
print('Tip: ${:.2f}, Total: ${:.2f}'.format(tip, bill+tip))
The way the format method works is we put a pair of curly braces {} anywhere that we want a formatted value. The arguments to the format function are the values we want formatted, with the first argument matching up with the first set of braces, the second argument with the second set of braces, etc. Inside each set of curly braces you can specify a formatting code to determine how the corresponding argument will be formatted.
Formatting integers
To format integers, the formatting code is {:d}. Putting a number in front of the d allows us to right-justify integers. Here is an example:
print('{:3d}'.format(2))
print('{:3d}'.format(25))
print('{:3d}'.format(138))
2 25 138
The number 3 in these examples says that the value is allotted three spots. The value is placed as far right in those three spots as possible and the rest of the slots will be filled by spaces. This sort of thing is useful for nicely formatting tables.
To center integers instead of right-justifying, use the ^ character, and to left-justify, use the < character.
print('{:^5d}'.format(2))
print('{:^5d}'.format(222))
print('{:^5d}'.format(13834))
2 122 13834
Each of these allots five spaces for the integer and centers it within those five spaces.
Putting a comma into the formatting code will format the integer with commas. The example below prints 1,000,000:
print('{:,d}'.format(1000000))
Formatting floats
To format a floating point number, the formatting code is {:f}. To only display the number to two decimal places, use {:.2f}. The 2 can be changed to change the number of decimal places.
You can right-justify floats. For example, {:8.2f} will allot eight spots for its value—one of those is for the decimal point and two are for the part of the value after the decimal point. If the value is 6.42, then only four spots are needed and the remaining spots are filled by spaces, causing the value to be right-justified.
The ^ and < characters center and left-justify floats.
Formatting strings
To format strings, the formatting code is {:s}. Here is an example that centers some text:
print('{:^10s}'.format('Hi'))
print('{:^10s}'.format('there!'))
Hi
there!
To right-justify a string, use the > character:
print('{:>6s}'.format('Hi'))
print('{:>6s}'.format('There'))
Hi
there!
There is a whole lot more that can be done with formatting. See the Python documentation.
Nested loops
You can put loops inside of other loops. A loop inside of another loop is said to be nested, and you can, more or less, nest loops as deeply as you want.
Example 1
Print a 10 × 10 multiplication table.
for i in range(1,11):
for j in range(1,11):
print('{:3d}'.format(i*j), end=' ')
print()
A multiplication table is a two-dimensional object. To work with it, we use two for loops, one for the horizontal direction and one for the vertical direction. The print statement right justifies the products to make them look nice. The end=' ' allows us to print several things on each row. When we are done printing a row, we use print() to advance things to the next line.
Example 2
A common math problem is to find the solutions to a system of equations. Sometimes you want to find only the integer solutions, and this can be a little tricky mathematically. However, we can write a program that does a brute force search for solutions. Here we find all the integer solutions (x,y) to the system 2x+3y=4, x-y=7, where x and y are both between -50 and 50.
for x in range(-50,51):
for y in range(-50,51):
if 2*x+3*y==4 and x-y==7:
print(x,y)
Example 3
A Pythagorean triple is a triple of numbers (x,y,z) such that x2+y2=z2. For instance (3,4,5) is a Pythagorean triple because 32+42=52. Pythagorean triples correspond to triangles whose sides are all whole numbers (like a 3-4-5-triangle). Here is a program that finds all the Pythagorean triples (x,y,z) where x, y, and z are positive and less than 100.
for x in range(1,100):
for y in range(1,100):
for z in range(1,100):
if x**2+y**2==z**2:
print(x,y,z)
If you run the program, you'll notice that there are redundant solutions. For instance, (3,4,5) and (4,3,5) are both listed. To get rid of these redundancies, change the second loop so that it runs from x to 100. This way, when x is 4, for instance, the first value for y that will be searched is 4, rather than 1, and so we won't get the redundant (4,3,5). Also change the third loop so that it runs from y to 100.
As you look through the solutions, you might also notice that there are many solutions that are multiples of others, like (6,8,10), and (9,12,15) are multiples of (3,4,5). The following program finds only primitive Pythagorean triples, those that aren't multiples of another triple. The way it does this is every time a new triple is found, it checks to make sure that x, y, and z are not all divisible by the same number.
for x in range(1,100):
for y in range(x,100):
for z in range(y,100):
if x**2+y**2==z**2:
for i in range(2,x):
if x%i==0 and y%i==0 and z%i==0:
break
else:
print((x,y,z), end=' ')
Example 4
In this section, we will write a game to play tic-tac-toe. The board is a 3 × 3 grid, and we will use nested for loops to create it.
Example 5
Your computer screen is grid of pixels. To draw images to the screen, we often use nested for loops—one loop for the horizontal direction, and one for the vertical direction. See this section and this one for examples.
Example 6
List comprehensions can contain nested for loops. The example below returns a list of all the vowels in a list of words.
[char for item in L for char in item if char in 'aeiou']
Exercises
- Write a program that uses
listandrangeto create the list[3, 6, 9,…, 99]. - Write a program that asks the user for a weight in kilograms. The program should convert the weight to kilograms, formatting the result to one decimal place.
- Write a program that asks the user to enter a word. Rearrange all the letters of the word in alphabetical order and print out the resulting word. For example,
abracadabrashould becomeaaaaabbcdrr. - Write a program that takes a list of ten prices and ten products, applies an 11% discount to each of the prices displays the output like below, right-justified and nicely formatted.
Apples $ 2.45 Oranges $ 18.02 ... Pears $120.03
- Use the following two lists and the
formatmethod to create a list of card names in the format card value of suit name (for example,'Two of Clubs').suits = ['Hearts', 'Diamonds', 'Clubs', 'Spades'] values = ['One', 'Two', 'Three', 'Four', 'Five', 'Six', 'Seven', 'Eight', 'Nine', 'Ten', 'Jack', 'Queen', 'King', 'Ace'] - Write a program that uses a boolean flag variable in determining whether two lists have any items in common.
- Write a program that creates the list
[1, 11, 111, 1111, ..., 111...1], where the entries have an ever increasing number of ones, with the last entry having 100 ones. - Write a program to find all numbers between 1 and 1000 that are divisible by 7 and end in a 6.
- Write a program to determine how many of the numbers between 1 and 10000 contain the digit 3.
- Adding certain numbers to their reversals sometimes produces a palindromic number. For instance, 241 + 142 = 383. Sometimes, we have to repeat the process. For instance, 84 + 48 = 132 and 132 + 231 = 363. Write a program that finds both two-digit numbers for which this process must be repeated more than 20 times to obtain a palindromic number.
- Write a program that finds all pairs of six-digit palindromic numbers that are less than 20 apart. One such pair is 199991 and 200002.
- The number 1961 reads the same upside-down as right-side up. Print out all the numbers between 1 and 100000 that read the same upside-down as right-side up.
- The number 99 has the property that if we multiply its digits together and then add the sum of its digits to that, we get back to 99. That is, (9 · 9) + (9 + 9) = 99. Write a program to find all of the numbers less than 10000 with this property. (There are only nine of them.)
- Write a program to find the smallest positive integer that satisfies the following property: If you take the leftmost digit and move it all the way to the right, the number thus obtained is exactly 3.5 times larger than the original number. For instance, if we start with 2958 and move the 2 all the way to the right, we get 9582, which is roughly 3.2 times the original number.
- Write a program to determine how many zeroes 1000! ends with.
- Write a program that converts a decimal height in feet into feet and inches. For instance, an input of
4.75feet should become4 feet,9 inches. - Write a program that repeatedly asks the user to enter a height in the format feet'inches" (like
5'11"or6'3". The user indicates they are done entering heights by enteringdone. The program should return a count of how many 4-footers, 5-footers, 6-footers, and 7-footers were entered. - Write a program that repeatedly asks the user to enter a football score in the format winning score-losing score (like
27-13or21-3). The user indicates they are done entering scores by enteringdone. The program should then output the highest score and the lowest score out of all the scores entered. - Write a program that repeatedly asks the user to enter a birthday in the format month/day (like
12/25or2/14). The user indicates they are done entering birthdays by enteringdone. The program should return a count of how many of those birthdays are in February and how many are on the 25th of some month (any month). - Write a program that asks the user to enter a date in the format
mm/dd/yyand converts it to a more verbose format. For example,02/04/77should get converted intoFebruary4,1977. - Write a program that asks the user to enter a fraction in the form of a string like
'1/2'or'8/24'. The program should reduce the fraction to lowest terms and print out the result. - Write a program to find all four solutions to the following problem: If a starfruit is worth $5, a mango is worth $3, and three oranges together cost $1, how many starfruits, mangoes, and oranges, totaling 100, can be bought for $100?
- The currency of a strange country has coins worth 7 cents and 11 cents. Write a program to determine the largest purchase price that cannot be paid using these two coins.
- Here is an old puzzle you can solve using brute force by using a computer program to check all the possibilities: In the calculation 43 + 57 = 207, every digit is precisely one away from its true value. What is the correct calculation?
- Write a program that finds all integer solutions to Pell's equation x2-2y2=1, where x and y are between 1 and 100.
- Write a program that asks the user for a number and prints out all the ways to write the number as difference of two perfect squares, x2-y2, where x and y are both between 1 and 1000. Writing a number as a difference of two squares leads to clever techniques for factoring large numbers.
- Write a program that simulates all possible rolls of four dice and for each simulated roll, finds the sums of pairs of dice. For instance, if the roll is 5 1 2 4, the sums are 6, 8, 9, 3 ,5, and 6. For each of the possible sums from 2 to 12, find the total number of simulated rolls in which the sum appears and what percentage of the simulated rolls had those sums appear. Output the totals and percentages, nicely formatted, with the percentages formatted to one decimal place. To check your work, you should find that the sum 2 comes up in 171 rolls, which is 13.2% of the rolls.
-
In a magic square, each row, each column, and both diagonals add up to the same number. A partially filled magic square is shown below. Write a program to check through all the possibilities to fill in the magic square.
5 _ _ _ 6 2 3 8 _
- The following is useful as part of a program to play Minesweeper. Suppose you have a 5 × 5 list that consists of zeros and M's. Write a program that creates a new 5 × 5 list that has M's in the same place, but the zeroes are replaced by counts of how many M's are in adjacent cells (adjacent either horizontally, vertically, or diagonally). An example is shown below. [Hint: short-circuiting may be helpful for avoiding index-out-of-range errors.]
0 M 0 M 0 1 M 3 M 1 0 0 M 0 0 1 2 M 2 1 0 0 0 0 0 2 3 2 1 0 M M 0 0 0 M M 2 1 1 0 0 0 M 0 2 2 2 M 1
- Pascal's triangle is shown below. On the outside are 1's and each other number is the sum of the two numbers directly above it.
Write a program to generate Pascal's triangle. Allow the user to specify the number of rows. Be sure that it is nicely formatted, like below.
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 - Given two dates entered as strings in the form mm/dd/yyyy where the years are between 1901 and 2099, determine how many days apart they are. Here is a bit of information that may be useful: Leap years between 1901 and 2099 occur exactly every four years, starting at 1904. February has 28 days, 29 during a leap year. November, April, June, and September each have 30 days. The other months have 31 days.
- Monte Carlo simulations can be used to estimate all sorts of things, including probabilities of coin flip and dice events. As an example, to estimate the probability of rolling a pair of sixes with two dice, we could use random integers to simulate the dice and run the simulation thousands of times, counting what percentage of the time a pair of sixes comes up.
- Estimate the probability of rolling a Yahtzee in a single roll of five dice. That is estimate the probability that when rolling five dice they all come out to be the same number.
- Estimate the probability of rolling a large straight in a single roll of five dice. A large straight is a roll where the dice come out 1-2-3-4-5 or 2-3-4-5-6 in any order.
- Estimate the average longest run of heads or tails when flipping a coin 200 times.
- Estimate the average number of coin flips it takes before five heads in a row come up.
- Estimate the average number of coin flips it takes before the string
scomes up, wheresis a string of heads and tails, likeHHTTH.
Dictionaries
A dictionary is a more general version of a list. Here is a list that contains the number of days in the months of the year:
days = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]
If we want the number of days in January, use days[0]. December is days[11] or days[-1].
Here is a dictionary of the days in the months of the year:
days = {'January':31, 'February':28, 'March':31, 'April':30,
'May':31, 'June':30, 'July':31, 'August':31,
'September':30, 'October':31, 'November':30, 'December':31}
To get the number of days in January, we use days['January']. One benefit of using dictionaries here is the code is more readable, and we don't have to figure out which index in the list a given month is at. Dictionaries have a number of other uses, as well.
Basics
Creating dictionaries
Here is a simple dictionary:
d = {'A':100, 'B':200}
To declare a dictionary we enclose it in curly braces, {}. Each entry consists of a pair separated by a colon. The first part of the pair is called the key and the second is the value. The key acts like an index. So in the first pair, 'A':100, the key is 'A', the value is 100, and d['A'] gives 100. Keys are often strings, but they can be integers, floats, and many other things as well. You can mix different types of keys in the same dictionary and different types of values, too.
Changing dictionaries
Let's start with this dictionary:
d = {'A':100, 'B':200}
- To change
d['A']to 400, dod['A']=400
-
To add a new entry to the dictionary, we can just assign it, like below:
d['C']=500
Note that this sort of thing does not work with lists. Doing
L[2]=500on a list with two elements would produce an index out of range error. But it does work with dictionaries. - To delete an entry from a dictionary, use the
deloperator:del d['A']
Empty dictionary
The empty dictionary is {}, which is the dictionary equivalent of [] for lists or ''; for strings.
Important note
The order of items in a dictionary will not necessarily be the order in which put them into the dictionary. Internally, Python rearranges things in a dictionary in order to optimize performance.
Dictionary examples
Example 1
You can use a dictionary as an actual dictionary of definitions:
d = {'dog' : 'has a tail and goes woof!',
'cat' : 'says meow',
'mouse' : 'chased by cats'}
Here is an example of the dictionary in use:
word = input('Enter a word: ')
print('The definition is:', d[word])
Enter a word: mouse The definition is: chased by cats
Example 2
The following dictionary is useful in a program that works with Roman numerals.
numerals = {'I':1, 'V':5, 'X':10, 'L':50, 'C':100, 'D':500, 'M':1000}
Example 3
In the game Scrabble, each letter has a point value associated with it. We can use the following dictionary for the letter values:
points = {'A':1, 'B':3, 'C':3, 'D':2, 'E':1, 'F':4, 'G':2,
'H':4, 'I':1, 'J':8, 'K':5, 'L':1, 'M':3, 'N':1,
'O':1, 'P':3, 'Q':10, 'R':1, 'S':1, 'T':1, 'U':1,
'V':4, 'W':4, 'X':8, 'Y':4, 'Z':10}
To score a word, we can do the following:
score = sum([points[c] for c in word])
Or, if you prefer the long way:
total = 0
for c in word:
total += points[c]
Example 4
A dictionary provides a nice way to represent a deck of cards:
deck = [{'value':i, 'suit':c}
for c in ['spades', 'clubs', 'hearts', 'diamonds']
for i in range(2,15)]
The deck is actually a list of 52 dictionaries. The shuffle method can be used to shuffle the deck:
shuffle(deck)
The first card in the deck is deck[0]. To get the value and the suit of the card, we would use the following:
deck[0]['value'] deck[0]['suit']
Working with dictionaries
Copying dictionaries
Just like for lists, making copies of dictionaries is a little tricky for reasons we will cover later. To copy a dictionary, use its copy method. Here is an example:
d2 = d.copy()
in
The in operator is used to tell if something is a key in the dictionary. For instance, say we have the following dictionary:
d = {'A':100, 'B':200}
Referring to a key that is not in the dictionary will produce an error. For instance, print(d['C']) will fail. To prevent this error, we can use the in operator to check first if a key is in the dictionary before trying to use the key. Here is an example:
letter = input('Enter a letter: ')
if letter in d:
print('The value is', d[letter])
else:
print('Not in dictionary')
You can also use not in to see if a key is not in the dictionary.
Looping
Looping through dictionaries is similar to looping through lists. Here is an example that prints the keys in a dictionary:
for key in d:
print(key)
Here is an example that prints the values:
for key in d:
print(d[key])
Lists of keys and values
The following table illustrates the ways to get lists of keys and values from a dictionary. It uses the dictionary d={'A':1, 'B':3}.
| Statement | Result | Description |
|---|---|---|
list(d) | ['A','B'] | keys of d |
list(d.values()) | [1,3] | values of d |
list(d.items()) | [('A',1),('B',3)] | (key,value) pairs of d |
d.items are called tuples. Tuples are a lot like lists. They are covered in this section.
Here is a use of d.items to find all the keys in a dictionary d that correspond to a value of 100:
d = {'A':100, 'B':200, 'C':100}
L = [x[0] for x in d.items() if x[1]==100]
['A', 'C']
dict
The dict function is another way to create a dictionary. One use for it is kind of like the opposite of the items method:
d = dict([('A',100),('B',300)])
This creates the dictionary {'A':100, 'B':300}. This way of building a dictionary is useful if your program needs to construct a dictionary while it is running.
Dictionary comprehensions
Dictionary comprehensions work similarly to list comprehensions. The following simple example creates a dictionary from a list of words, where the values are the lengths of the words:
d = {s : len(s) for s in words}
Counting words
We can use dictionaries to count how frequently certain words appear in a text.
In this section, we will learn how to read from a text file. For now, here's a line of code that reads the entire contents of a file containing the text of Shakespeare's Romeo and Juliet and stores the contents in a string called text:
text = open('romeoandjuliet.txt').read()
To get at the individual words, we will use the split method to turn the string into a list of its individual words. Also, because some words may be capitalized, we will convert the whole string to lowercase. We also have to remove punctuation.
from string import punctuation
text = text.lower()
for p in punctuation:
text = text.replace(p, '';)
words = text.split()
Next comes the dictionary code that does the counting. The dictionary keys will be the words from the text and the values will be counts of how many time each word appears. We start with an empty dictionary. Then for every word in the list of words, if we have seen the word before, we add one to its count, and otherwise we set the count for that word equal to 1. Here is the code:
d = {}
for w in words:
if w in d:
d[w] = d[w] + 1
else:
d[w] = 1
Once we have created the dictionary, we can use the following code to print the items in alphabetical order:
items = list(d.items())
items.sort()
for i in items:
print(i)
The way this works is a little tricky. Remember that d.items() returns a list of pairs (called tuples), which are a lot like lists. When we sort a list of tuples, the sorting is done by the first entry, which in this case is the word. So the sorting is done alphabetically.
If we instead want to order things by frequency, we can flip the order of the tuples and then sort:
items = list(d.items())
items = [(i[1], i[0]) for i in items]
items.sort()
for i in items:
print(i)
Here is the code all together:
from string import punctuation
# read from file, remove caps and punctuation, and split into words
text = open('romeoandjuliet.txt').read()
text = text.lower()
for p in punctuation:
text = text.replace(p, '';)
words = text.split()
# build the dictionary of frequencies
d = {}
for w in words:
if w in d:
d[w] = d[w] + 1
else:
d[w] = 1
# print in alphabetical order
items = list(d.items())
items.sort()
for i in items:
print(i)
# print in order from least to most common
items = list(d.items())
items = [(i[1], i[0]) for i in items]
items.sort()
for i in items:
print(i)
See this section for another approach to word frequencies.
Exercises
- Write a program that repeatedly asks the user to enter product names and prices. Store all of these in a dictionary whose keys are the product names and whose values are the prices. When the user is done entering products and prices, allow them to repeatedly enter a product name and print the corresponding price or a message if the product is not in the dictionary.
- Using the dictionary created in the previous problem, allow the user to enter a dollar amount and print out all the products whose price is less than that amount.
- For this problem, use the dictionary from the beginning of this chapter whose keys are month names and whose values are the number of days in the corresponding months.
- Ask the user to enter a month name and use the dictionary to tell them how many days are in the month.
- Print out all of the keys in alphabetical order.
- Print out all of the months with 31 days.
- Print out the (key-value) pairs sorted by the number of days in each month
- Modify the program from part (a) and the dictionary so that the user does not have to know how to spell the month name exactly. That is, all they have to do is spell the first three letters of the month name correctly.
- Write a program that uses a dictionary that contains ten user names and passwords. The program should ask the user to enter their username and password. If the username is not in the dictionary, the program should indicate that the person is not a valid user of the system. If the username is in the dictionary, but the user does not enter the right password, the program should say that the password is invalid. If the password is correct, then the program should tell the user that they are now logged in to the system.
- Repeatedly ask the user to enter a team name and the how many games the team won and how many they lost. Store this information in a dictionary where the keys are the team names and the values are lists of the form
[wins,losses].- Using the dictionary created above, allow the user to enter a team name and print out the team's winning percentage.
- Using the dictionary, create a list whose entries are the number of wins of each team.
- Using the dictionary, create a list of all those teams that have winning records.
- Repeatedly ask the user to enter game scores in a format like team1 score1 - team2 score2. Store this information in a dictionary where the keys are the team names and the values are lists of the form
[wins,losses]. - Create a 5 × 5 list of numbers. Then write a program that creates a dictionary whose keys are the numbers and whose values are the how many times the number occurs. Then print the three most common numbers.
- Using the card dictionary from earlier in this chapter, create a simple card game that deals two players three cards each. The player with the highest card wins. If there is a tie, then compare the second highest card and, if necessary, the third highest. If all three cards have the same value, then the game is a draw.
- Using the card dictionary from earlier in the chapter, deal out three cards. Determine the following:
- If the three cards form a flush (all of the same suit)
- If there is a three-of-a-kind (all of the same value)
- If there is a pair, but not three-of-a-kind
- If the three cards form a straight (all in a row, like (2, 3, 4) or (10, Jack, Queen))
- Using the card dictionary from earlier in the chapter run a Monte Carlo simulation to estimate the probability of being dealt a flush in a five card hand. See this exercise for more about Monte Carlo simulations.
- In this section we met the substitution cipher. This cipher replaces every letter with a different letter. For instance every a might be replaced with an e, every b might be replaced with an a, etc. Write a program that asks the user to enter two strings. Then determine if the second string could be an encoded version of the first one with a substitution cipher. For instance, CXYZ is not an encoded version of BOOK because O got mapped to two separate letters. Also, CXXK is not an encoded version of BOOK, because K got mapped to itself. On the other hand, CXXZ would be an encoding of BOOK. This problem can be done with or without a dictionary.
- Below are the notes used in music:
C C# D D# E F F# G G# A A# B
The notes for the C major chord are C, E, G. A mathematical way to get this is that E is 4 steps past C and G is 7 steps past C. This works for any base. For example, the notes for D major are D, F#, A. We can represent the major chord steps as a list with two elements:
[4, 7]. The corresponding lists for some other chord types are shown below:Minor [3,7]Dominant seventh [4,7,10]Augmented fifth [4,8]Minor seventh [3,7,10]Minor fifth [4,6]Major seventh [4,7,11]Major sixth [4,7,9]Diminished seventh [3,6,10]Minor sixth [3,7,9]Write a program that asks the user for the key and the chord type and prints out the notes of the chord. Use a dictionary whose keys are the (musical) keys and whose values are the lists of steps.
- Suppose you are given the following list of strings:
L = ['aabaabac', 'cabaabca', 'aaabbcba', 'aabacbab', 'acababba']
Patterns like this show up in many places, including DNA sequencing. The user has a string of their own with only some letters filled in and the rest as asterisks. An example is
a**a****. The user would like to know which of the strings in the list fit with their pattern. In the example just given, the matching strings are the first and fourth. One way to solve this problem is to create a dictionary whose keys are the indices in the user's string of the non-asterisk characters and whose values are those characters. Write a program implementing this approach (or some other approach) to find the strings that match a user-entered string. - Dictionaries provide a convenient way to store structured data. Here is an example dictionary:
d=[{'name':'Todd', 'phone':'555-1414', 'email':'todd@mail.net'}, {'name':'Helga', 'phone':'555-1618', 'email':'helga@mail.net'}, {'name':'Princess', 'phone':'555-3141', 'email':'';}, {'name':'LJ', 'phone':'555-2718', 'email':'lj@mail.net'}]Write a program that reads through any dictionary like this and prints the following:
- All the users whose phone number ends in an 8
- All the users that don't have an email address listed
- The following problem is from the string chapter. Try it again, this time using a dictionary whose keys are the names of the time zones and whose values are offsets from the Eastern time zone.
Write a program that converts a time from one time zone to another. The user enters the time in the usual American way, such as
3:48pmor11:26am. The first time zone the user enters is that of the original time and the second is the desired time zone. The possible time zones areEastern,Central,Mountain, orPacific.Time: 11:48pm Starting zone: Pacific Ending zone: Eastern 2:48am
-
- Write a program that converts Roman numerals into ordinary numbers. Here are the conversions: M=1000, D=500, C=100, L=50, X=10, V=5 I=1. Don't forget about things like IV being 4 and XL being 40.
- Write a program that converts ordinary numbers into Roman numerals
Text Files
There is a ton of interesting data to be found on the internet stored in text files. In this chapter we will learn how to work with data stored in text files.
Reading from files
Suppose we have a text file called example.txt whose contents are shown below, and we want to read its contents into Python. There are several ways to do so. We will look at two of them.
Hello. This is a text file. Bye!
- The first way to read a text file uses a list comprehension to load the file line-by-line into a list:
lines = [line.strip() for line in open('example.txt')]The list
linesis now['Hello.', 'This is a text file.', 'Bye!']
The string method
stripremoves any whitespace characters from the beginning and end of a string. If we had not used it, each line would contain a newline character at the end of the line. This is usually not what we want.Note:
stripremoves whitespace from both the beginning and end of the line. Userstripif you need to preserve whitespace at the beginning of the line. - The second way of reading a text file loads the entire file into a string:
s = open('example.txt').read()The string
sis now'Hello.\nThis is a text file.\nBye!'
Directories
Say your program opens a file, like below:
s = open('file.txt').read()
The file is assumed to be in the same directory as your program itself. If it is in a different directory, then you need to specify that, like below:
s = open('c:/users/heinold/desktop/file.txt').read()
Writing to files
There are also several ways to write to files. We will look at one way here. We will be writing to a file called writefile.txt.
f = open('writefile.txt', 'w')
print('This is line 1.', file=f)
print('This is line 2.', file=f)
f.close()
We first have to open the file. That is what the first line does, with the 'w' indicating that we want to be able to write to the file. Python creates what is called a file object to represent the file, and we give that object the name f. This is what we use to refer to the file. To write to the file, we use the print statement with the optional file argument that specifies the file to write to. When we are done writing, we should close the file to make sure all of our changes take. Be careful here because if writefile.txt already exists, its contents will be overwritten.
Examples
Example 1
Write a program that reads a list of temperatures from a file called temps.txt, converts those temperatures to Fahrenheit, and writes the results to a file called ftemps.txt.
file1 = open('ftemps.txt', 'w')
temperatures = [line.strip() for line in open('temps.txt')]
for t in temperatures:
print(int(t)*9/5+32, file=file1)
file1.close()
Example 2
In this section we wrote a simple quiz game. The questions and answers were both contained in lists hard-coded into the program. Instead of that, we can store the questions and answers in files. That way, if you decide to change the questions or answers, you just have to change their files. Moreover, if you decide to give the program to someone else who doesn't know Python, they can easily create their own lists of questions and answers. To do this, we just replace the lines that create the lists with the following:
questions = [line.strip() for line in open('questions.txt')]
answers = [line.strip() for line in open('answers.txt')]
Example 3
Say you have a text file that contains the results of every 2009-10 NCAA basketball game. (You can find such a file here.) A typical line of the file looks like this:
02/27/2010, Robert Morris, 61, Mount St. Mary's, 63
Below is a program that scans through the file to find the most lopsided game, the one where the winning team had the largest margin of victory.
lines = [line.strip() for line in open('scores.txt')]
games = [line.split(',') for line in lines]
print(max([abs(int(g[2])-int(g[4])) for g in games]))
We use the split method to break each line into a lists of its component parts. The scores are at indices 2 and 4. To find the maximum difference, we can use a list comprehension to create a list of all the margins of victories and use max to find the maximum.
The maximum turns out to be 84. Unfortunately, the method above does not tell us anything else about the game. In order to do that, we resort to the longer way to find maximums, described in this section. This allows us to store information about the game as we search for the largest margin of victory.
lines = [line.strip() for line in open('scores.txt')]
games = [line.split(',') for line in lines]
biggest_diff = 0
for g in games:
diff = abs(int(g[2])-int(g[4]))
if diff>biggest_diff:
biggest_diff = diff
game_info = g
print(game_info)
['12/03/2009', ' SalemInternational', '35', ' Marshall', '119']
Wordplay
If you like words, you can have a lot of fun with a wordlist, which is a text file where each line contains a different word. A quick web search will turn up a variety of different wordlists, ranging from lists of common English words to lists containing practically every English word.
Assuming the wordlist file is wordlist.txt, we can load the words into a list using the line below.
wordlist = [line.strip() for line in open('wordlist.txt')]
Example 1
Print all three letter words.
for word in wordlist:
if len(word)==3:
print(word)
Note that this and most of the upcoming examples can be done with list comprehensions:
print([word for word in wordlist if len(word)==3])
Example 2
Print all the words that start with gn or kn.
for word in wordlist:
if word[:2]=='gn' or word[:2]=='kn':
print(word)
Example 3
Determine what percentage of words start with a vowel.
count = 0
for word in wordlist:
if word[0] in 'aeiou':
count=count+1
print(100*count/len(wordlist))
Example 4
Print all 7-letter words that start with th and end in ly. Things like this are good for cheating at crosswords.
for word in wordlist:
if len(word)==7 and word[:2]=='th' and word[-2:]=='ly':
print(word)
Example 5
Print the first ten words that start with q.
i=0
while wordlist[i][0]!='q':
i=i+1
print(wordlist[i:i+10]
Note this is not a very efficient way of doing things since we have to scan through most of the list. A binary search would be more efficient, but the above approach still runs almost instantly even for large files.
Example 6
Find the longest word that can be made using only the letters a, b, c, d, and e.
largest = 0
for word in wordlist:
for c in word:
if c not in 'abcde':
break
else:
if len(word)>largest:
largest=len(word)
largest_word=word
print(largest_word)
The way this program works is for every word in the wordlist, we use a for/else loop to scan through the word looking checking each character to see if it is an a, b, c, d, or e. If any letter isn't one of these, then we break out of the loop and move on to the next word. On the other hand, if we get all the way through the loop, then we go to else block. In that block, we use a modification of the technique from this section for finding a maximum.
Exercises
- You are given a file called
class_scores.txt, where each line of the file contains a one-word username and a test score separated by spaces, like below:.GWashington 83 JAdams 86
Write code that scans through the file, adds 5 points to each test score, and outputs the usernames and new test scores to a new file,
scores2.txt. - You are given a file called
grades.txt, where each line of the file contains a one-word student username and three test scores separated by spaces, like below:.GWashington 83 77 54 JAdams 86 69 90
Write code that scans through the file and determines how many students passed all three tests.
- You are given a file called
logfile.txtthat lists log-on and log-off times for users of a system. A typical line of the file looks like this:Van Rossum, 14:22, 14:37
Each line has three entries separated by commas: a username, a log-on time, and a log-off time. Times are given in 24-hour format. You may assume that all log-ons and log-offs occur within a single workday.
Write a program that scans through the file and prints out all users who were online for at least an hour.
- You are given a file called
students.txt. A typical line in the file looks like:walter melon melon@email.msmary.edu 555-3141
There is a name, an email address, and a phone number, each separated by tabs. Write a program that reads through the file line-by-line, and for each line, capitalizes the first letter of the first and last name and adds the area code 301 to the phone number. Your program should write this to a new file called
students2.txt. Here is what the first line of the new file should look like:Walter Melon melon@email.msmary.edu 301-555-3141
- You are given a file
namelist.txtthat contains a bunch of names. Some of the names are a first name and a last name separated by spaces, like George Washington, while others have a middle name, like John Quincy Adams. There are no names consisting of just one word or more than three words. Write a program that asks the user to enter initials, like GW or JQA, and prints all the names that match those initials. Note that initials like JA should match both John Adams and John Quincy Adams. - You are given a file
namelist.txtthat contains a bunch of names. Print out all the names in the list in which the vowels a, e, i, o, and u appear in order (with repeats possible). The first vowel in the name must be a and after the first u, it is okay for there to be other vowels. An example is Ace Elvin Coulson. - You are given a file called
baseball.txt. A typical line of the file starts like below.Ichiro Suzuki SEA 162 680 74 ...[more stats]
Each entry is separated by a tab,
\t. The first entry is the player's name and the second is their team. Following that are 16 statistics. Home runs are the seventh stat and stolen bases are the eleventh. Print out all the players who have at least 20 home runs and at least 20 stolen bases. - For this problem, use the file of NCAA basketball scores as described in Section this section.
- Find the average of the points scored over all the games in the file.
- Pick your favorite team and scan through the file to determine how many games they won and how many games they lost.
- Find the team(s) that lost by 30 or more points the most times
- Find all the teams that averaged at least 70 points a game.
- Find all the teams that had winning records but were collectively outscored by their opponents. A team is collectively outscored by their opponents if the total number of points the team scored over all their games is less than the total number of points their opponents scored in their games against the team.
- Benford's law states that in real data where the values are spread across several orders of magnitude, about 30% of the values will start with the number 1, whereas only about 4.6% of the values will start with the number 9. This is contrary to what we might expect, namely that values starting with 1 and 9 would be equally likely. Using the file
expenses.txtwhich consists of a number of costs from an expense account, determine what percentage start with each of the digits 1 through 9. This technique is used by accountants to detect fraud. - Wordplay -- Use the file
wordlist.txtfor this problem. Find the following:- All words ending in ime
- All words whose second, third, and fourth letters are ave
- How many words contain at least one of the letters r, s, t, l, n, e
- The percentage of words that contain at least one of the letters r, s, t, l, n, e
- All words with no vowels
- All words that contain every vowel
- Whether there are more ten-letter words or seven-letter words
- The longest word in the list
- All palindromes
- All words that are words in reverse, like rat and tar.
- Same as above, but only print one word out of each pair.
- All words that contain double letters next each other like aardvark or book, excluding words that end in lly
- All words that contain a q that isn't followed by a u
- All words that contain zu anywhere in the word
- All words that contain ab in multiple places, like habitable
- All words with four or more vowels in a row
- All words that contain both a z and a w
- All words whose first letter is a, third letter is e and fifth letter is i
- All two-letter words
- All four-letter words that start and end with the same letter
- All words that contain at least nine vowels.
- All words that contain each of the letters a, b, c, d, e, and f in any order. There may be other letters in the word. Two examples are backfield and feedback.
- All words whose first four and last four letters are the same
- All words of the form abcd*dcba, where * is arbitrarily long sequence of letters.
- All groups of 5 words, like pat pet pit pot put, where each word is 3 letters, all words share the same first and last letters, and the middle letter runs through all 5 vowels.
- The word that has the most i's.
- Write a program to help with word games. The user enters a word and the program uses the wordlist to determine if the user's word is a real word or not.
- Suppose we write all the words in the wordlist backwards and then arrange these backwards words alphabetically. Write a program that prints the last word in this modified wordlist.
-
Print out all combinations of the string
'Python'plus a three letter English word. Capitalize the first letter of the three letter word. Example combinations are'PythonCat','PythonDog', and'PythonTag'. These are valid combinations because cat, dog, and tag are English words. On the other hand,'PythonQqz'would not be a valid combination because qqz is not an English word. Use a wordlist to determine which three letter combinations are words. - Write a simple spell-checking program. The user should enter a string and the program should print out a list of all the words it thinks are misspelled. These would be all the words it cannot find in a wordlist.
-
Crossword cheater: When working on a crossword puzzle, often you will have a word where you know several of the letters, but not all of them. You can write a computer program to help you. For the program, the user should be able to input a word with the letters they know filled in and asterisks for those they don't know. The program should print out a list of all words that fit that description. For example, the input
th***lyshould return all the words that could work, namely thickly and thirdly. - Ask the user to enter several letters. Then find all the words that can be made with those letters, repeats allowed.
- Using the wordlist, produce a dictionary whose keys are the letters a through z and whose values are the percentage of words that use that letter.
- Using the wordlist, produce a dictionary whose keys are the letters a through z and whose values are the percentage of total letters in the wordlist that are that letter.
- Write a program that asks the user for a word and finds all the smaller words that can be made from the letters of that word. The number of occurrences of a letter in a smaller word can't exceed the number of occurrences of the letter in the user's word.
-
-
Write a program that reads a file consisting of email addresses, each on its own line. Your program should print out a string consisting of those email addresses separated by semicolons.
-
Write the same program as above, but the new string should contain only those email addresses that do not end in
@prof.college.edu.
-
- The file
high_temperatures.txtcontains the average high temperatures for each day of the year in a certain city. Each line of the file consists of the date, written in the month/day format, followed by a space and the average high temperature for that date. Find the 30-day period over which there is the biggest increase in the average high temperature. - In the string chapter there was an exercise about the game Mad Libs. It asked you to make up a story and leave out some words of the story. Your program should ask the user to enter some words and tell them what types of words to enter. Then print the full story along with the inserted words. Rewrite your program from that exercise to read the story from a file. Reading the story from a file allows people who do not know how to program to use their own stories with the program without having to change the code.
-
An acronym is an abbreviation that uses the first letter of each word in a phrase. We see them everywhere. For instance, NCAA for National Collegiate Athletic Association or NBC for National Broadcasting Company. Write a program where the user enters an acronym and the program randomly selects words from a wordlist such that the words would fit the acronym. Below is some typical output generated when I ran the program:
Enter acronym: ABC ['addressed', 'better', 'common'] Enter acronym: BRIAN ['bank', 'regarding', 'intending', 'army', 'naive']
- This problem is about a version of the game Jotto. The computer chooses a random five-letter word with no repeat letters. The player gets several turns to try to guess the computer's word. On each turn, the player guesses a five-letter word and is told the number of letters that their guess has in common with the computer's word.
- The word part has the interesting property that if you remove its letters one by one, each resulting step is a real word. For instance, part → pat → pa → a. You may remove the letters in any order, and the last (single-letter) word needs to be a real word as well. Find all eight-letter words with this property.
- Write a program to cheat at the game Scrabble. The user enters a string. Your program should return a list of all the words that can be created from those seven letters.
Functions
Functions are useful for breaking up a large program to make it easier to read and maintain. They are also useful if you find yourself writing the same code at several different points in your program. You can put that code in a function and call the function whenever you want to execute that code. You can also use functions to create your own utilities, math functions, etc.
Basics
Functions are defined with the def statement. The statement ends with a colon, and the code that is part of the function is indented below the def statement. Here we create a simple function that just prints something.
def print_hello():
print('Hello!')
print_hello()
print('1234567')
print_hello()
Hello! 1234567 Hello!
The first two lines define the function. In the last three lines we call the function twice.
One use for functions is if you are using the same code over and over again in various parts of your program, you can make your program shorter and easier to understand by putting the code in a function. For instance, suppose for some reason you need to print a box of stars like the one below at several points in your program.
************** * * * * **************
Put the code into a function, and then whenever you need a box, just call the function rather than typing several lines of redundant code. Here is the function.
def draw_square():
print('*' * 15)
print('*', ' '*11, '*')
print('*', ' '*11, '*')
print('*' * 15)
One benefit of this is that if you decide to change the size of the box, you just have to modify the code in the function, whereas if you had copied and pasted the box-drawing code everywhere you needed it, you would have to change all of them.
Arguments
We can pass values to functions. Here is an example:
def print_hello(n):
print('Hello ' * n)
print()
print_hello(3)
print_hello(5)
times = 2
print_hello(times)
Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello
When we call the print_hello function with the value 3, that value gets stored in the variable n. We can then refer to that variable n in our function's code.
You can pass more than one value to a function:
def multiple_print(string, n):
print(string * n)
print()
multiple_print('Hello', 5)
multiple_print('A', 10)
HelloHelloHelloHelloHello AAAAAAAAAA
Returning values
We can write functions that perform calculations and return a result.
Example 1
Here is a simple function that converts temperatures from Celsius to Fahrenheit.
def convert(t):
return t*9/5+32
print(convert(20))
68
The return statement is used to send the result of a function's calculations back to the caller.
Notice that the function itself does not do any printing. The printing is done outside of the function. That way, we can do math with the result, like below.
print(convert(20)+5)
If we had just printed the result in the function instead of returning it, the result would have been printed to the screen and forgotten about, and we would never be able to do anything with it.
Example 2
As another example, the Python math module contains trig functions, but they only work in radians. Let us write our own sine function that works in degrees.
from math import pi, sin
def deg_sin(x):
return sin(pi*x/180)
Example 3
A function can return multiple values as a list.
Say we want to write a function that solves the system of equations ax+by=e and cx+dy=f. It turns out that if there is a unique solution, then it is given by x=(de-bf)/(ad-bc) and y=(af-ce)/(ad-bc). We need our function to return both the x and y solutions.
def solve(a,b,c,d,e,f):
x = (d*e-b*f)/(a*d-b*c)
y = (a*f-c*e)/(a*d-b*c)
return [x,y]
xsol, ysol = solve(2,3,4,1,2,5)
print('The solution is x = ', xsol, 'and y = ', ysol)
The solution is x = 1.3 and y = -0.2
This method uses the shortcut for assigning to lists that was mentioned in this section.
Example 4
A return statement by itself can be used to end a function early.
def multiple_print(string, n, bad_words):
if string in bad_words:
return
print(string * n)
print()
The same effect can be achieved with an if/else statement, but in some cases, using return can make your code simpler and more readable.
Default arguments and keyword arguments
You can specify a default value for an argument. This makes it optional, and if the caller decides not to use it, then it takes the default value. Here is an example:
def multiple_print(string, n=1)
print(string * n)
print()
multiple_print('Hello', 5)
multiple_print('Hello')
HelloHelloHelloHelloHello Hello
Default arguments need to come at the end of the function definition, after all of the non-default arguments.
Keyword arguments
A related concept to default arguments is keyword arguments. Say we have the following function definition:
def fancy_print(text, color, background, style, justify):
Every time you call this function, you have to remember the correct order of the arguments. Fortunately, Python allows you to name the arguments when calling the function, as shown below:
fancy_print(text='Hi', color='yellow', background='black',
style='bold', justify='left')
fancy_print(text='Hi', style='bold', justify='left',
background='black', color='yellow')
As we can see, the order of the arguments does not matter when you use keyword arguments.
When defining the function, it would be a good idea to give defaults. For instance, most of the time, the caller would want left justification, a white background, etc. Using these values as defaults means the caller does not have to specify every single argument every time they call the function. Here is a example:
def fancy_print(text, color='black', background='white',
style='normal', justify='left'):
# function code goes here
fancy_print('Hi', style='bold')
fancy_print('Hi', color='yellow', background='black')
fancy_print('Hi')
Note
We have actually seen default and keyword arguments before—the sep, end and file arguments of the print function.
Local variables
Let's say we have two functions like the ones below that each use a variable i:
def func1():
for i in range(10):
print(i)
def func2():
i=100
func1()
print(i)
A problem that could arise here is that when we call func1, we might mess up the value of i in func2. In a large program it would be a nightmare trying to make sure that we don't repeat variable names in different functions, and, fortunately, we don't have to worry about this. When a variable is defined inside a function, it is local to that function, which means it essentially does not exist outside that function. This way each function can define its own variables and not have to worry about if those variable names are used in other functions.
Global variables
On the other hand, sometimes you actually do want the same variable to be available to multiple functions. Such a variable is called a global variable. You have to be careful using global variables, especially in larger programs, but a few global variables used judiciously are fine in smaller programs. Here is a short example:
def reset():
global time_left
time_left = 0
def print_time():
print(time_left)
time_left=30
In this program we have a variable time_left that we would like multiple functions to have access to. If a function wants to change the value of that variable, we need to tell the function that time_left is a global variable. We use a global statement in the function to do this. On the other hand, if we just want to use the value of the global variable, we do not need a global statement.
Arguments
We finish the chapter with a bit of a technical detail. You can skip this section for the time being if you don't want to worry about details right now. Here are two simple functions:
def func1(x):
x = x + 1
def func2(L):
L = L + [1]
a=3
M=[1,2,3]
func1(a)
func2(M)
When we call func1 with a and func2 with L, a question arises: do the functions change the values of a and L? The answer may surprise you. The value of a is unchanged, but the value of L is changed. The reason has to do with a difference in the way that Python handles numbers and lists. Lists are said to be mutable objects, meaning they can be changed, whereas numbers and strings are immutable, meaning they cannot be changed. There is more on this in this section.
If we want to reverse the behavior of the above example so that a is modified and L is not, do the following:
def func1(x):
x = x + 1
return x
def func2(L):
copy = L[:]
copy = copy + [1]
a=3
M=[1,2,3]
a=func1(a) # note change on this line
func2(M)
Exercises
- Write a function called
rectanglethat takes two integersmandnas arguments and prints out an m × n box consisting of asterisks. Shown below is the output ofrectangle(2,4)**** ****
-
- Write a function called
add_excitementthat takes a list of strings and adds an exclamation point (!) to the end of each string in the list. The program should modify the original list and not return anything. - Write the same function except that it should not modify the original list and should instead return a new list.
- Write a function called
- Write a function called
sum_digitsthat is given an integernumand returns the sum of the digits ofnum. - The digital root of a number n is obtained as follows: Add up the digits n to get a new number. Add up the digits of that to get another new number. Keep doing this until you get a number that has only one digit. That number is the digital root. For example, if n=45893, we add up the digits to get 4+5+8+9+3 = 29. We then add up the digits of 29 to get 2+9=11. We then add up the digits of 11 to get 1+1=2. Since 2 has only one digit, 2 is our digital root. Write a function that returns the digital root of an integer n. [Note: there is a shortcut, where the digital root is equal to n mod 9, but do not use that here.]
- Write a function called
first_diffthat is given two strings and returns the first location in which the strings differ. If the strings are identical, it should return -1. - Write a function called
binomthat takes two integers n and k and returns the binomial coefficient n C k. The definition is n C k = n!/(k!(n-k)!). - Write a function that takes an integer n and returns a random integer with exactly n digits. For instance, if n is 3, then 125 and 593 would be valid return values, but 093 would not because that is really 93, which is a two-digit number.
- Write a function called
number_of_factorsthat takes an integer and returns how many factors the number has. - Write a function called
factorsthat takes an integer and returns a list of its factors. - Write a function called
closestthat takes a list of numbersLand a numbernand returns the largest element inLthat is not larger thann. For instance, ifL=[1,6,3,9,11]andn=8, then the function should return 6, because 6 is the closest thing inLto 8 that is not larger than 8. Don't worry about if all of the things inLare smaller thann. - Write a function called
matchesthat takes two strings as arguments and returns how many matches there are between the strings. A match is where the two strings have the same character at the same index. For instance,'python'and'path'match in the first, third, and fourth characters, so the function should return 3. - Recall that if
sis a string, thens.find('a')will find the location of the first a ins. The problem is that it does not find the location of every a. Write a function calledfindallthat given a string and a single character, returns a list containing all of the locations of that character in the string. It should return an empty list if there are no occurrences of the character in the string. - Write a function called
change_casethat given a string, returns a string with each upper case letter replaced by a lower case letter and vice-versa. - Write a function called
is_sortedthat is given a list and returnsTrueif the list is sorted andFalseotherwise. - Write a function called
rootthat is given a number x and an integer n and returns x1/n. In the function definition, set the default value of n to 2. - Write a function called
one_awaythat takes two strings and returnsTrueif the strings are of the same length and differ in exactly one letter, likebike/hikeorwater/wafer. -
- Write a function called
primesthat is given a number n and returns a list of the first n primes. Let the default value of n be 100. - Modify the function above so that there is an optional argument called
startthat allows the list to start at a value other than 2. The function should return the first n primes that are greater than or equal tostart. The default value ofstartshould be 2.
- Write a function called
- Our number system is called base 10 because we have ten digits: 0, 1, …, 9. Some cultures, including the Mayans and Celts, used a base 20 system. In one version of this system, the 20 digits are represented by the letters A through T. Here is a table showing a few conversions:
10 20 10 20 10 20 10 20 0 A 8 I 16 Q 39 BT 1 B 9 J 17 R 40 CA 2 C 10 K 18 S 41 CB 3 D 11 L 19 T 60 DA 4 E 12 M 20 BA 399 TT 5 F 13 N 21 BB 400 BAA 6 G 14 O 22 BC 401 BAB 7 H 15 P 23 BD 402 BAC Write a function called
base20that converts a base 10 number to base 20. It should return the result as a string of base 20 digits. One way to convert is to find the remainder when the number is divided by 20, then divide the number by 20, and repeat the process until the number is 0. The remainders are the base 20 digits in reverse order, though you have to convert them into their letter equivalents. - Write a function called
verbosethat, given an integer less than 1015, returns the name of the integer in English. As an example,verbose(123456)should returnonehundredtwenty-threethousand,fourhundredfifty-six. - Write a function called
mergethat takes two already sorted lists of possibly different lengths, and merges them into a single sorted list.- Do this using the
sortmethod. - Do this without using the
sortmethod.
- Do this using the
- In the chapter on text files, the way we checked to see if a word
wwas a real word was:if w in words:
where
wordswas the list of words generated from a wordlist. This is unfortunately slow, but there is a faster way, called a binary search. To implement a binary search in a function, start by comparingwwith the middle entry inwords. If they are equal, then you are done and the function should returnTrue. On the other hand, ifwcomes before the middle entry, then search the first half of the list. If it comes after the middle entry, then search the second half of the list. Then repeat the process on the appropriate half of the list and continue until the word is found or there is nothing left to search, in which case the function short returnFalse. The<and>operators can be used to alphabetically compare two strings. - A Tic-tac-toe board can be represented be a 3 × 3 two-dimensional list, where zeroes stand for empty cells, ones stand for X's and twos stand for O's.
- Write a function that is given such a list and randomly chooses a spot in which to place a 2. The spot chosen must currently be a 0 and a spot must be chosen.
- Write a function that is given such a list and checks to see if someone has won. Return
Trueif there is a winner andFalseotherwise.
- Write a function that is given a 9 × 9 potentially solved Sudoku and returns
Trueif it is solved correctly andFalseif there is a mistake. The Sudoku is correctly solved if there are no repeated numbers in any row or any column or in any of the nine “blocks.”
Object-Oriented Programming
About a year or so after I started programming, I decided to make a game to play Wheel of Fortune. I wrote the program in the BASIC programming language and it got to be pretty large, a couple thousand lines. It mostly worked, but whenever I tried to fix something, my fix would break something in a completely different part of the program. I would then fix that and break something else. Eventually I got the program working, but after a while I was afraid to even touch it.
The problem with the program was that each part of the program had access to the variables from the other parts. A change of a variable in one part would mess up things in the others. One solution to this type of problem is object-oriented programming. One of its chief benefits is encapsulation, where you divide your program into pieces and each piece internally operates independently of the others. The pieces interact with each other, but they don't need to know exactly how each one accomplishes its tasks. This requires some planning and set-up time before you start your program, and so it is not always appropriate for short programs, like many of the ones that we have written so far.
We will just cover the basics of object-oriented programming here. Object-oriented programming is used extensively in software design and I would recommend picking up another book on programming or software design to learn more about designing programs in an object-oriented way.
Python is objected-oriented
Python is an object-oriented programming language, and we have in fact been using many object-oriented concepts already. The key notion is that of an object. An object consists of two things: data and functions (called methods) that work with that data. As an example, strings in Python are objects. The data of the string object is the actual characters that make up that string. The methods are things like lower, replace, and split. In Python, everything is an object. That includes not only strings and lists, but also integers, floats, and even functions themselves.
Creating your own classes
A class is a template for objects. It contains the code for all the object's methods.
A simple example
Here is a simple example to demonstrate what a class looks like. It does not do anything interesting.
class Example:
def __init__(self, a, b):
self.a = a
self.b = b
def add(self):
return self.a + self.b
e = Example(8, 6)
print(e.add())
- To create a class, we use the
classstatement. Class names usually start with a capital. - Most classes will have a method called
__init__. The underscores indicate that it is a special kind of method. It is called a constructor, and it is automatically called when someone creates a new object from your class. The constructor is usually used to set up the class's variables. In the above program, the constructor takes two values,aandb, and assigns the class variablesaandbto those values. - The first argument to every method in your class is a special variable called
self. Every time your class refers to one of its variables or methods, it must precede them byself. The purpose ofselfis to distinguish your class's variables and methods from other variables and functions in the program. - To create a new object from the class, you call the class name along with any values that you want to send to the constructor. You will usually want to assign it to a variable name. This is what the line
e=Example(8, 6)does. - To use the object's methods, use the dot operator, as in
e.addmod().
A more practical example
Here is a class called Analyzer that performs some simple analysis on a string. There are methods to return how many words are in the string, how many are of a given length, and how many start with a given string.
from string import punctuation
class Analyzer:
def __init__(self, s):
for c in punctuation:
s = s.replace(c,'';)
s = s.lower()
self.words = s.split()
def number_of_words(self):
return len(self.words)
def starts_with(self, s):
return len([w for w in self.words if w[:len(s)]==s])
def number_with_length(self, n):
return len([w for w in self.words if len(w)==n])
s = 'This is a test of the class.'
analyzer = Analyzer(s)
print(analyzer.words)
print('Number of words:', analyzer.number_of_words())
print('Number of words starting with "t":', analyzer.starts_with('t'))
print('Number of 2-letter words:', analyzer.number_with_length(2))
['this', 'is', 'a', 'test', 'of', 'the', 'class'] Number of words: 7 Number of words starting with "t": 3 Number of 2-letter words: 2
A few notes about this program:
- One reason why we would wrap this code up in a class is we can then use it a variety of different programs. It is also good just for organizing things. If all our program is doing is just analyzing some strings, then there's not too much of a point of writing a class, but if this were to be a part of a larger program, then using a class provides a nice way to separate the
Analyzercode from the rest of the code. It also means that if we were to change the internals of theAnalyzerclass, the rest of the program would not be affected as long as the interface, the way the rest of the program interacts with the class, does not change. Also, theAnalyzerclass can be imported as-is in other programs. - The following line accesses a class variable:
print(analyzer.words)
You can also change class variables. This is not always a good thing. In some cases this is convenient, but you have to be careful with it. Indiscriminate use of class variables goes against the idea of encapsulation and can lead to programming errors that are hard to fix. Some other object-oriented programming languages have a notion of public and private variables, public variables being those that anyone can access and change, and private variables being only accessible to methods within the class. In Python all variables are public, and it is up to the programmer to be responsible with them. There is a convention where you name those variables that you want to be private with a starting underscore, like
_var1. This serves to let others know that this variable is internal to the class and shouldn't be touched.
Inheritance
In object-oriented programming there is a concept called inheritance where you can create a class that builds off of another class. When you do this, the new class gets all of the variables and methods of the class it is inheriting from (called the base class). It can then define additional variables and methods that are not present in the base class, and it can also override some of the methods of the base class. That is, it can rewrite them to suit its own purposes. Here is a simple example:
class Parent:
def __init__(self, a):
self.a = a
def method1(self):
return self.a*2
def method2(self):
return self.a+'!!!'
class Child(Parent):
def __init__(self, a, b):
self.a = a
self.b = b
def method1(self):
return self.a*7
def method3(self):
return self.a + self.b
p = Parent('hi')
c = Child('hi', 'bye')
print('Parent method 1: ', p.method1())
print('Parent method 2: ', p.method2())
print()
print('Child method 1: ', c.method1())
print('Child method 2: ', c.method2())
print('Child method 3: ', c.method3())
Parent method 1: hihi Parent method 2: hi!!! Child method 1: hihihihihihihi Child method 2: hi!!! Child method 3: hibye
We see in the example above that the child has overridden the parent's method1, causing it to now repeat the string seven times. The child has inherited the parent's method2, so it can use it without having to define it. The child also adds some features to the parent class, namely a new variable b and a new method, method3.
A note about syntax: when inheriting from a class, you indicate the parent class in parentheses in the class statement.
If the child class adds some new variables, it can call the parent class's constructor as demonstrated below. Another use is if the child class just wants to add on to one of the parent's methods. In the example below, the child's print_var method calls the parent's print_var method and adds an additional line.
class Parent:
def __init__(self, a):
self.a = a
def print_var(self):
print("The value of this class's variables are:")
print(self.a)
class Child(Parent):
def __init__(self, a, b):
Parent.__init__(self, a)
self.b = b
def print_var(self):
Parent.print_var(self)
print(self.b)
Note
You can also inherit from Python built-in types, like strings (str) and lists (list), as well as any classes defined in the various modules that come with Python.
Note
Your code can inherit from more than one class at a time, though this can be a little tricky.A playing-card example
In this section we will show how to design a program with classes. We will create a simple hi-lo card game where the user is given a card and they have to say if the next card will be higher or lower than it. This game could easily be done without classes, but we will create classes to represent a card and a deck of cards, and these classes can be reused in other card games.
We start with a class for a playing card. The data associated with a card consists of its value (2 through 14) and its suit. The Card class below has only one method, __str__. This is a special method that, among other things, tells the print function how to print a Card object.
class Card:
def __init__(self, value, suit):
self.value = value
self.suit = suit
def __str__(self):
names = ['Jack', 'Queen', 'King', 'Ace']
if self.value <= 10:
return '{} of {}'.format(self.value, self.suit)
else:
return '{} of {}'.format(names[self.value-11], self.suit)
Next we have a class to represent a group of cards. Its data consists of a list of Card objects. It has a number of methods: nextCard which removes the first card from the list and returns it; hasCard which returns True or False depending on if there are any cards left in the list; size, which returns how many cards are in the list; and shuffle, which shuffles the list.
import random
class Card_group:
def __init__(self, cards=[]):
self.cards = cards
def nextCard(self):
return self.cards.pop(0)
def hasCard(self):
return len(self.cards)>0
def size(self):
return len(self.cards)
def shuffle(self):
random.shuffle(self.cards)
We have one more class Standard_deck, which inherits from Card_group. The idea here is that Card_group represents an arbitrary group of cards, and Standard_deck represents a specific group of cards, namely the standard deck of 52 cards used in most card games.
class Standard_deck(Card_group):
def __init__(self):
self.cards = []
for s in ['Hearts', 'Diamonds', 'Clubs', 'Spades']:
for v in range(2,15):
self.cards.append(Card(v, s))
Suppose we had just created a single class that represented a standard deck along with all the common operations like shuffling. If we wanted to create a new class for a Pinochle game or some other game that doesn't use the standard deck, then we would have to copy and paste the standard deck code and modify lots of things. By doing things more generally, like we've done here, each time we want a new type of deck, we can build off of (inherit from) what is in Card_group. For instance, a Pinochle deck class would look like this:
class Pinochle_deck(Card_group):
def __init__(self):
self.cards = []
for s in ['Hearts', 'Diamonds', 'Clubs', 'Spades']*2:
for v in range(9,15):
self.cards.append(Card(v, s))
A Pinochle deck has only nines, tens, jacks, queens, kings, and aces. There are two copies of each card in each suit.
Here is the hi-low program that uses the classes we have developed here. One way to think of what we have done with the classes is that we have built up a miniature card programming language, where we can think about how a card game works and not have to worry about exactly how cards are shuffled or dealt or whatever, since that is wrapped up into the classes. For the hi-low game, we get a new deck of cards, shuffle it, and then deal out the cards one at a time. When we run out of cards, we get a new deck and shuffle it. A nice feature of this game is that it deals out all 52 cards of a deck, so a player can use their memory to help them play the game.
deck = Standard_deck()
deck.shuffle()
new_card = deck.nextCard()
print('\n', new_card)
choice = input("Higher (h) or lower (l): ")
streak = 0
while (choice=='h' or choice=='l'):
if not deck.hasCard():
deck = Standard_deck()
deck.shuffle()
old_card = new_card
new_card = deck.nextCard()
if (choice.lower()=='h' and new_card.value>old_card.value or\
choice.lower()=='l' and new_card.value<old_card.value):
streak = streak + 1
print("Right! That's", streak, "in a row!")
elif (choice.lower()=='h' and new_card.value<old_card.value or\
choice.lower()=='l' and new_card.value>old_card.value):
streak = 0
print('Wrong.')
else:
print('Push.')
print('\n', new_card)
choice = input("Higher (h) or lower (l): ")
King of Clubs Higher (h) or lower (l): l Right! That's 1 in a row! 2 of Spades Higher (h) or lower (l): h Right! That's 2 in a row!
A Tic-tac-toe example
In this section we create an object-oriented Tic-tac-toe game. We use a class to wrap up the logic of the game. The class contains two variables, an integer representing the current player, and a 3 × 3 list representing the board. The board variable consists of zeros, ones, and twos. Zeros represent an open spot, while ones and twos represent spots marked by players 1 and 2, respectively. There are four methods:
-
get_open_spots— returns a list of the places on the board that have not yet been marked by players -
is_valid_move— takes a row and a column representing a potential move, and returnsTrueif move is allowed andFalseotherwise -
make_move— takes a row and a column representing a potential move, callsis_valid_moveto see if the move is okay, and if it is, sets the board array accordingly and changes the player -
check_for_winner— scans through the board list and returns 1 if player 1 has won, 2 if player 2 has won, 0 if there are no moves remaining and no winner, and -1 if the game should continue
Here is the code for the class:
class tic_tac_toe:
def __init__(self):
self.B = [[0,0,0],
[0,0,0],
[0,0,0]]
self.player = 1
def get_open_spots(self):
return [[r,c] for r in range(3) for c in range(3)
if self.B[r][c]==0]
def is_valid_move(self,r,c):
if 0<=r<=2 and 0<=c<=2 and self.B[r][c]==0:
return True
return False
def make_move(self,r,c):
if self.is_valid_move(r,c):
self.B[r][c] = self.player
self.player = (self.player+2)%2 + 1
def check_for_winner(self):
for c in range(3):
if self.B[0][c]==self.B[1][c]==self.B[2][c]!=0:
return self.B[0][c]
for r in range(3):
if self.B[r][0]==self.B[r][1]==self.B[r][2]!=0:
return self.B[r][0]
if self.B[0][0]==self.B[1][1]==self.B[2][2]!=0:
return self.B[0][0]
if self.B[2][0]==self.B[1][1]==self.B[0][2]!=0:
return self.B[2][0]
if self.get_open_spots()==[]:
return 0
return -1
This class consists of the logic of the game. There is nothing in the class that is specific to the user interface. Below we have a text-based interface using print and input statements. If we decide to use a graphical interface, we can use the Tic_tac_toe class without having to change anything about it. Note that the get_open_spots method is not used by this program. It is useful, however, if you want to implement a computer player. A simple computer player would call that method and use random.choice method to choose a random element from the returned list of spots.
def print_board():
chars = ['-', 'X', 'O']
for r in range(3):
for c in range(3):
print(chars[game.B[r][c]], end=' ')
print()
game = tic_tac_toe()
while game.check_for_winner()==-1:
print_board()
r,c = eval(input('Enter spot, player ' + str(game.player) + ': '))
game.make_move(r,c)
print_board()
x = game.check_for_winner()
if x==0:
print("It's a draw.")
else:
print('Player', x, 'wins!')
Here is what the first couple of turns look like:
- - - - - - - - - Enter spot, player 1: 1,1 - - - - X - - - - Enter spot, player 2: 0,2 - - O - X - - - - Enter spot, player 1:
Further topics
-
Special methods —
We have seen two special methods already, the constructor
__init__and the method__str__which determines what your objects look like when printed. There are many others. For instance, there is__add__that allows your object to use the+operator. There are special methods for all the Python operators. There is also a method called__len__which allows your object to work with the built inlenfunction. There is even a special method,__getitem__that lets your program work with list and string brackets[]. -
Copying objects —
If you want to make a copy of an object
x, it is not enough to do the following:x_copy = x
The reason is discussed in this section. Instead, do the following:
from copy import copy x_copy = copy(x)
-
Keeping your code in multiple files — If you want to reuse a class in several programs, you do not have to copy and paste the code into each. You can save it in a file and use an import statement to import it into your programs. The file will need to be somewhere your program can find it, like in the same directory.
from analyzer import Analyzer
Exercises
- Write a class called
Investmentwith fields calledprincipalandinterest. The constructor should set the values of those fields. There should be a method calledvalue_afterthat returns the value of the investment after n years. The formula for this is p(1+i)n, where p is the principal, and i is the interest rate. It should also use the special method__str__so that printing the object will result in something like below:Principal - $1000.00, Interest rate - 5.12%
- Write a class called
Product. The class should have fields calledname,amount, andprice, holding the product's name, the number of items of that product in stock, and the regular price of the product. There should be a methodget_pricethat receives the number of items to be bought and returns a the cost of buying that many items, where the regular price is charged for orders of less than 10 items, a 10% discount is applied for orders of between 10 and 99 items, and a 20% discount is applied for orders of 100 or more items. There should also be a method calledmake_purchasethat receives the number of items to be bought and decreasesamountby that much. - Write a class called
Password_manager. The class should have a list calledold_passwordsthat holds all of the user's past passwords. The last item of the list is the user's current password. There should be a method calledget_passwordthat returns the current password and a method calledset_passwordthat sets the user's password. Theset_passwordmethod should only change the password if the attempted password is different from all the user's past passwords. Finally, create a method calledis_correctthat receives a string and returns a booleanTrueorFalsedepending on whether the string is equal to the current password or not. - Write a class called
Timewhose only field is a time in seconds. It should have a method calledconvert_to_minutesthat returns a string of minutes and seconds formatted as in the following example: if seconds is 230, the method should return'5:50'. It should also have a method calledconvert_to_hoursthat returns a string of hours, minutes, and seconds formatted analogously to the previous method. - Write a class called
Wordplay. It should have a field that holds a list of words. The user of the class should pass the list of words they want to use to the class. There should be the following methods:-
words_with_length(length)— returns a list of all the words of lengthlength -
starts_with(s)— returns a list of all the words that start withs -
ends_with(s)— returns a list of all the words that end withs -
palindromes()— returns a list of all the palindromes in the list -
only(L)— returns a list of the words that contain only those letters inL -
avoids(L)— returns a list of the words that contain none of the letters inL
-
- Write a class called
Converter. The user will pass a length and a unit when declaring an object from the class—for example,c = Converter(9, 'inches'). The possible units are inches, feet, yards, miles, kilometers, meters, centimeters, and millimeters. For each of these units there should be a method that returns the length converted into those units. For example, using theConverterobject created above, the user could callc.feet()and should get0.75as the result. - Use the
Standard_deckclass of this section to create a simplified version of the game War. In this game, there are two players. Each starts with half of a deck. The players each deal the top card from their decks and whoever has the higher card wins the other player's cards and adds them to the bottom of his deck. If there is a tie, the two cards are eliminated from play (this differs from the actual game, but is simpler to program). The game ends when one player runs out of cards. - Write a class that inherits from the
Card_groupclass of this chapter. The class should represent a deck of cards that contains only hearts and spaces, with only the cards 2 through 10 in each suit. Add a method to the class callednext2that returns the top two cards from the deck. - Write a class called
Rock_paper_scissorsthat implements the logic of the game Rock-paper-scissors. For this game the user plays against the computer for a certain number of rounds. Your class should have fields for the how many rounds there will be, the current round number, and the number of wins each player has. There should be methods for getting the computer's choice, finding the winner of a round, and checking to see if someone has one the (entire) game. You may want more methods. -
- Write a class called
Connect4that implements the logic of a Connect4 game. Use theTic_tac_toeclass from this chapter as a starting point. - Use the
Connect4class to create a simple text-based version of the game.
- Write a class called
- Write a class called
Poker_handthat has a field that is a list ofCardobjects. There should be the following self-explanatory methods:has_royal_flush, has_straight_flush, has_four_of_a_kind, has_full_house, has_flush, has_straight, has_three_of_a_kind, has_two_pair, has_pair
There should also be a method called
bestthat returns a string indicating what the best hand is that can be made from those cards.
PART II: GRAPHICS
GUI Programming with Tkinter
Up until now, the only way our programs have been able to interact with the user is through keyboard input via the input statement. But most real programs use windows, buttons, scrollbars, and various other things. These widgets are part of what is called a Graphical User Interface or GUI. This chapter is about GUI programming in Python with Tkinter.
All of the widgets we will be looking at have far more options than we could possibly cover here. An excellent reference is Fredrik Lundh's Introduction to Tkinter.
Basics
Nearly every GUI program we will write will contain the following three lines:
from tkinter import * root = Tk() mainloop()
The first line imports all of the GUI stuff from the tkinter module. The second line creates a window on the screen, which we call root. The third line puts the program into what is essentially a long-running while loop called the event loop. This loop runs, waiting for keypresses, button clicks, etc., and it exits when the user closes the window.
Here is a working GUI program that converts temperatures from Fahrenheit to Celsius.
from tkinter import *
def calculate():
temp = int(entry.get())
temp = 9/5*temp+32
output_label.configure(text = 'Converted: {:.1f}'.format(temp))
entry.delete(0,END)
root = Tk()
message_label = Label(text='Enter a temperature',
font=('Verdana', 16))
output_label = Label(font=('Verdana', 16))
entry = Entry(font=('Verdana', 16), width=4)
calc_button = Button(text='Ok', font=('Verdana', 16),
command=calculate)
message_label.grid(row=0, column=0)
entry.grid(row=0, column=1)
calc_button.grid(row=0, column=2)
output_label.grid(row=1, column=0, columnspan=3)
mainloop()
Here is what the program looks like:
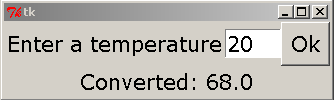
We now will examine the components of the program separately.
Labels
A label is a place for your program to place some text on the screen. The following code creates a label and places it on the screen.
hello_label = Label(text='hello') hello_label.grid(row=0, column=0)
We call Label to create a new label. The capital L is required. Our label's name is hello_label. Once created, use the grid method to place the label on the screen. We will explain grid in the next section.
Options
There are a number of options you can change including font size and color. Here are some examples:
hello_label = Label(text='hello', font=('Verdana', 24, 'bold'),
bg='blue', fg='white')
Note the use of keyword arguments. Here are a few common options:
-
font— The basic structure isfont=(font name, font size, style). You can leave out the font size or the style. The choices for style are'bold','italic','underline','overstrike','roman', and'normal'(which is the default). You can combine multiple styles like this:'bold italic'. -
fgandbg— These stand forforegroundandbackground. Many common color names can be used, like'blue','green', etc. This section describes how to get essentially any color. -
width— This is how many characters long the label should be. If you leave this out, Tkinter will base the width off of the text you put in the label. This can make for unpredictable results, so it is good to decide ahead of time how long you want your label to be and set thewidthaccordingly. -
height— This is how many rows high the label should be. You can use this for multi-line labels. Use newline characters in the text to get it to span multiple lines. For example,text='hi\nthere'.
There are dozens more options. The aforementioned Introduction to Tkinter has a nice list of the others and what they do.
Changing label properties
Later in your program, after you've created a label, you may want to change something about it. To do that, use its configure method. Here are two examples that change the properties of a label called label:
label.configure(text='Bye') label.configure(bg='white', fg='black')
Setting text to something using the configure method is kind of like the GUI equivalent of a print statement. However, in calls to configure we cannot use commas to separate multiple things to print. We instead need to use string formatting. Here is a print statement and its equivalent using the configure method.
print('a =', a, 'and b =', b)
label.configure(text='a = {}, and b = {}'.format(a,b))
The configure method works with most of the other widgets we will see.
grid
The grid method is used to place things on the screen. It lays out the screen as a rectangular grid of rows and columns. The first few rows and columns are shown below.
(row=0, column=0) | (row=0, column=1) | (row=0, column=2) |
(row=1, column=0) | (row=1, column=1) | (row=1, column=2) |
(row=2, column=0) | (row=2, column=1) | (row=2, column=2) |
Spanning multiple rows or columns
There are optional arguments, rowspan and columnspan, that allow a widget to take up more than one row or column. Here is an example of several grid statements followed by what the layout will look like:
) label1.grid(row=0, column=0) label2.grid(row=0, column=1) label3.grid(row=1, column=0, columnspan=2) label4.grid(row=1, column=2) label5.grid(row=2, column=2)
label1 | label2 | |
label 3 | label4 | |
label5 | ||
Spacing
To add extra space between widgets, there are optional arguments padx and pady.
Important note
Any time you create a widget, to place it on the screen you need to usegrid (or one of its cousins, like pack, which we will talk about later). Otherwise it will not be visible.
Entry boxes
Entry boxes are a way for your GUI to get text input. The following example creates a simple entry box and places it on the screen.
entry = Entry() entry.grid(row=0, column=0)
Most of the same options that work with labels work with entry boxes (and most of the other widgets we will talk about). The width option is particularly helpful because the entry box will often be wider than you need.
- Getting text
To get the text from an entry box, use its
getmethod. This will return a string. If you need numerical data, useeval(orintorfloat) on the string. Here is a simple example that gets text from an entry box namedentry.string_value = entry.get() num_value = eval(entry.get())
- Deleting text To clear an entry box, use the following:
entry.delete(0,END)
- Inserting textTo insert text into an entry box, use the following:
entry.insert(0, 'hello')
Buttons
The following example creates a simple button:
ok_button = Button(text='Ok')
To get the button to do something when clicked, use the command argument. It is set to the name of a function, called a callback function. When the button is clicked, the callback function is called. Here is an example:
from tkinter import *
def callback():
label.configure(text='Button clicked')
root = Tk()
label = Label(text='Not clicked')
button = Button(text='Click me', command=callback)
label.grid(row=0, column=0)
button.grid(row=1, column=0)
mainloop()
When the program starts, the label says Click me. When the button is clicked, the callback function callback is called, which changes the label to say Button clicked.
lambda trick
Sometimes we will want to pass information to the callback function, like if we have several buttons that use the same callback function and we want to give the function information about which button is being clicked. Here is an example where we create 26 buttons, one for each letter of the alphabet. Rather than use 26 separate Button() statements and 26 different functions, we use a list and one function.
from tkinter import *
alphabet = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
def callback(x):
label.configure(text='Button {} clicked'.format(alphabet[x]))
root = Tk()
label = Label()
label.grid(row=1, column=0, columnspan=26)
buttons = [0]*26 # create a list to hold 26 buttons
for i in range(26):
buttons[i] = Button(text=alphabet[i],
command = lambda x=i: callback(x))
buttons[i].grid(row=0, column=i)
mainloop()
We note a few things about this program. First, we set buttons = [0]*26. This creates a list with 26 things in it. We don't really care what thoset things are because they will be replaced with buttons. An alternate way to create the list would be to set buttons = [] and use the append method.

We only use one callback function and it has one argument, which indicates which button was clicked. As far as the lambda trick goes, without getting into the details, command=callback(i) does not work, and that is why we resort to the lambda trick. You can read more about lambda in this section. An alternate approach is to use classes.
Global variables
Let's say we want to keep track of how many times a button is clicked. An easy way to do this is to use a global variable as shown below.
from tkinter import *
def callback():
global num_clicks
num_clicks = num_clicks + 1
label.configure(text='Clicked {} times.'.format(num_clicks))
num_clicks = 0
root = Tk()
label = Label(text='Not clicked')
button = Button(text='Click me', command=callback)
label.grid(row=0, column=0)
button.grid(row=1, column=0)
mainloop()
We will be using a few global variables in our GUI programs. Using global variables unnecessarily, especially in long programs, can cause difficult to find errors that make programs hard to maintain, but in the short programs that we will be writing, we should be okay. Object-oriented programming provides an alternative to global variables.
Tic-tac-toe
Using Tkinter, in only about 20 lines we can make a working tic-tac-toe program:
from tkinter import *
def callback(r,c):
global player
if player == 'X':
b[r][c].configure(text = 'X')
player = 'O'
else:
b[r][c].configure(text = 'O')
player = 'X'
root = Tk()
b = [[0,0,0],
[0,0,0],
[0,0,0]]
for i in range(3):
for j in range(3):
b[i][j] = Button(font=('Verdana', 56), width=3, bg='yellow',
command = lambda r=i,c=j: callback(r,c))
b[i][j].grid(row = i, column = j)
player = 'X'
mainloop()
The program works, though it does have a few problems, like letting you change a cell that already has something in it. We will fix this shortly. First, let's look at how the program does what it does. Starting at the bottom, we have a variable player that keeps track of whose turn it is. Above that we create the board, which consists of nine buttons stored in a two-dimensional list. We use the lambda trick to pass the row and column of the clicked button to the callback function. In the callback function we write an X or an O into the button that was clicked and change the value of the global variable player.

Correcting the problems
To correct the problem about being able to change a cell that already has something in it, we need to have a way of knowing which cells have X's, which have O's, and which are empty. One way is to use a Button method to ask the button what its text is. Another way, which we will do here is to create a new two-dimensional list, which we will call states, that will keep track of things. Here is the code.
from tkinter import *
def callback(r,c):
global player
if player == 'X' and states[r][c] == 0:
b[r][c].configure(text='X')
states[r][c] = 'X'
player = 'O'
if player == 'O' and states[r][c] == 0:
b[r][c].configure(text='O')
states[r][c] = 'O'
player = 'X'
root = Tk()
states = [[0,0,0],
[0,0,0],
[0,0,0]]
b = [[0,0,0],
[0,0,0],
[0,0,0]]
for i in range(3):
for j in range(3):
b[i][j] = Button(font=('Verdana', 56), width=3, bg='yellow',
command = lambda r=i,c=j: callback(r,c))
b[i][j].grid(row = i, column = j)
player = 'X'
mainloop()
We have not added much to the program. Most of the new action happens in the callback function. Every time someone clicks on a cell, we first check to see if it is empty (that the corresponding index in states is 0), and if it is, we display an X or O on the screen and record the new value in states. Many games have a variable like states that keeps track of what is on the board.
Checking for a winner
We have a winner when there are three X's or three O's in a row, either vertically, horizontally, or diagonally. To check if there are three in a row across the top row, we can use the following if statement:
if states[0][0]==states[0][1]==states[0][2]!=0:
stop_game=True
b[0][0].configure(bg='grey')
b[0][1].configure(bg='grey')
b[0][2].configure(bg='grey')
This checks to see if each of the cells has the same nonzero entry. We are using the shortcut from this section here in the if statement. There are more verbose if statements that would work. If we do find a winner, we highlight the winning cells and then set a global variable stop_game equal to True. This variable will be used in the callback function. Whenever the variable is True we should not allow any moves to take place.
Next, to check if there are three in a row across the middle row, change the first coordinate from 0 to 1 in all three references, and to check if there are three in a row across the bottom, change the 0's to 2's. Since we will have three very similar if statements that only differ in one location, a for loop can be used to keep the code short:
for i in range(3):
if states[i][0]==states[i][1]==states[i][2]!=0:
b[i][0].configure(bg='grey')
b[i][1].configure(bg='grey')
b[i][2].configure(bg='grey')
stop_game = True
Next, checking for vertical winners is pretty much the same except we vary the second coordinate instead of the first. Finally, we have two further if statements to take care of the diagonals. The full program is at the end of this chapter. We have also added a few color options to the configure statements to make the game look a little nicer.
Further improvements
From here it would be easy to add a restart button. The callback function for that variable should set stop_game back to false, it should set states back to all zeroes, and it should configure all the buttons back to text=''; and bg='yellow'.
To add a computer player would also not be too difficult, if you don't mind it being a simple computer player that moves randomly. That would take about 10 lines of code. To make an intelligent computer player is not too difficult. Such a computer player should look for two O's or X's in a row in order to try to win or block, as well avoid getting put into a no-win situation.
from tkinter import *
def callback(r,c):
global player
if player == 'X' and states[r][c] == 0 and stop_game==False:
b[r][c].configure(text='X', fg='blue', bg='white')
states[r][c] = 'X'
player = 'O'
if player == 'O' and states[r][c] == 0 and stop_game==False:
b[r][c].configure(text='O', fg='orange', bg='black')
states[r][c] = 'O'
player = 'X'
check_for_winner()
def check_for_winner():
global stop_game
for i in range(3):
if states[i][0]==states[i][1]==states[i][2]!=0:
b[i][0].configure(bg='grey')
b[i][1].configure(bg='grey')
b[i][2].configure(bg='grey')
stop_game = True
for i in range(3):
if states[0][i]==states[1][i]==states[2][i]!=0:
b[0][i].configure(bg='grey')
b[1][i].configure(bg='grey')
b[2][i].configure(bg='grey')
stop_game = True
if states[0][0]==states[1][1]==states[2][2]!=0:
b[0][0].configure(bg='grey')
b[1][1].configure(bg='grey')
b[2][2].configure(bg='grey')
stop_game = True
if states[2][0]==states[1][1]==states[0][2]!=0:
b[2][0].configure(bg='grey')
b[1][1].configure(bg='grey')
b[0][2].configure(bg='grey')
stop_game = True
root = Tk()
b = [[0,0,0],
[0,0,0],
[0,0,0]]
states = [[0,0,0],
[0,0,0],
[0,0,0]]
for i in range(3):
for j in range(3):
b[i][j] = Button(font=('Verdana', 56), width=3, bg='yellow',
command = lambda r=i,c=j: callback(r,c))
b[i][j].grid(row = i, column = j)
player = 'X'
stop_game = False
mainloop()
GUI Programming II
In this chapter we cover more basic GUI concepts.
Frames
Let's say we want 26 small buttons across the top of the screen, and a big Ok button below them, like below:
We try the following code:
from tkinter import *
root = Tk()
alphabet = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
buttons = [0]*26
for i in range(26):
buttons[i] = Button(text=alphabet[i])
buttons[i].grid(row=0, column=i)
ok_button = Button(text='Ok', font=('Verdana', 24))
ok_button.grid(row=1, column=0)
mainloop()
But we instead get the following unfortunate result:
The problem is with column 0. There are two widgets there, the A button and the Ok button, and Tkinter will make that column big enough to handle the larger widget, the Ok button. One solution to this problem is shown below:
ok_button.grid(row=1, column=0, columnspan=26)
Another solution to this problem is to use what is called a frame. The frame's job is to hold other widgets and essentially combine them into one large widget. In this case, we will create a frame to group all of the letter buttons into one large widget. The code is shown below:
from tkinter import *
alphabet = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
root = Tk()
button_frame = Frame()
buttons = [0]*26
for i in range(26):
buttons[i] = Button(button_frame, text=alphabet[i])
buttons[i].grid(row=0, column=i)
ok_button = Button(text='Ok', font=('Verdana', 24))
button_frame.grid(row=0, column=0)
ok_button.grid(row=1, column=0)
mainloop()
To create a frame, we use Frame() and give it a name. Then, for any widgets we want include in the frame, we include the name of the frame as the first argument in the widget's declaration. We still have to grid the widgets, but now the rows and columns will be relative to the frame. Finally, we have to grid the frame itself.
Colors
Tkinter defines many common color names, like 'yellow' and 'red'. It also provides a way to get access to millions of more colors. We first have to understand how colors are displayed on the screen.
Each color is broken into three components—a red, a green, and a blue component. Each component can have a value from 0 to 255, with 255 being the full amount of that color. Equal parts of red and green create shades of yellow, equal parts of red and blue create shades of purple, and equal parts of blue and green create shades of turquoise. Equal parts of all three create shades of gray. Black is when all three components have values of 0 and white is when all three components have values of 255. Varying the values of the components can produce up to 2563≈ 16 million colors. There are a number of resources on the web that allow you to vary the amounts of the components and see what color is produced.
To use colors in Tkinter is easy, but with one catch—component values are given in hexadecimal. Hexadecimal is a base 16 number system, where the letters A-F are used to represent the digits 10 through 15. It was widely used in the early days of computing, and it is still used here and there. Here is a table comparing the two number bases:
| 0 | 0 | 8 | 8 | 16 | 10 | 80 | 50 |
| 1 | 1 | 9 | 9 | 17 | 11 | 100 | 64 |
| 2 | 2 | 10 | A | 18 | 12 | 128 | 80 |
| 3 | 3 | 11 | B | 31 | 1F | 160 | A0 |
| 4 | 4 | 12 | C | 32 | 20 | 200 | C8 |
| 5 | 5 | 13 | D | 33 | 21 | 254 | FE |
| 6 | 6 | 14 | E | 48 | 30 | 255 | FF |
| 7 | 7 | 15 | F | 64 | 40 | 256 | 100 |
Because the color component values run from 0 to 255, they will run from 0 to FF in hexadecimal, and thus are described by two hex digits. A typical color in Tkinter is specified like this: '#A202FF'. The color name is prefaced with a pound sign. Then the first two digits are the red component (in this case A2, which is 162 in decimal). The next two digits specify the green component (here 02, which is 2 in decimal), and the last two digits specify the blue component (here FF, which is 255 in decimal). This color turns out to be a bluish violet. Here is an example of it in use:
label = Label(text='Hi', bg='#A202FF')
If you would rather not bother with hexadecimal, you can use the following function which will convert percentages into the hex string that Tkinter uses.
def color_convert(r, g, b):
return '#{:02x}{:02x}{:02x}'.format(int(r*2.55),int(g*2.55),
int(b*2.55))
Here is an example of it to create a background color that has 100% of the red component, 85% of green and 80% of blue.
label = Label(text='Hi', bg=color_convert(100, 85, 80))
Images
Labels and buttons (and other widgets) can display images instead of text.
To use an image requires a little set-up work. We first have to create a PhotoImage object and give it a name. Here is an example:
cheetah_image = PhotoImage(file='cheetahs.gif')
Here are some examples of putting the image into widgets:
label = Label(image=cheetah_image) button = Button(image=cheetah_image, command=cheetah_callback())
You can use the configure method to set or change an image:
label.configure(image=cheetah_image)
File types
One unfortunate limitation of Tkinter is the only common image file type it can use is GIF. If you would like to use other types of files, one solution is to use the Python Imaging Library, which will be covered in this section.Canvases
A canvas is a widget on which you can draw things like lines, circles, rectangles. You can also draw text, images, and other widgets on it. It is a very versatile widget, though we will only describe the basics here.
Creating canvases
The following line creates a canvas with a white background that is 200 × 200 pixels in size:
canvas = Canvas(width=200, height=200, bg='white')
Rectangles
The following code draws a red rectangle to the canvas:
canvas.create_rectangle(20,100,30,150, fill='red')
See the image below on the left. The first four arguments specify the coordinates of where to place the rectangle on the canvas. The upper left corner of the canvas is the origin, (0,0). The upper left of the rectangle is at (20,100), and the lower right is at (30,150). If were to leave off fill='red', the result would be a rectangle with a black outline.
Ovals and lines
Drawing ovals and lines is similar. The image above on the right is created with the following code:
canvas.create_rectangle(20,100,70,180) canvas.create_oval(20,100,70,180, fill='blue') canvas.create_line(20,100,70,180, fill='green')
The rectangle is here to show that lines and ovals work similarly to rectangles. The first two coordinates are the upper left and the second two are the lower right.
To get a circle with radius r and center (x,y), we can create the following function:
def create_circle(x,y,r):
canvas.create_oval(x-r,y-r,x+r,y+r)
Images
We can add images to a canvas. Here is an example:
cheetah_image = PhotoImage(file='cheetahs.gif') canvas.create_image(50,50, image=cheetah_image)
The two coordinates are where the center of the image should be.
Naming things, changing them, moving them, and deleting them
We can give names to the things we put on the canvas. We can then use the name to refer to the object in case we want to move it or remove it from the canvas. Here is an example were we create a rectangle, change its color, move it, and then delete it:
rect = canvas.create_rectangle(0,0,20,20) canvas.itemconfigure(rect, fill='red') canvas.coords(rect,40,40,60,60) canvas.delete(rect)
The coords method is used to move or resize an object and the delete method is used to delete it. If you want to delete everything from the canvas, use the following:
canvas.delete(ALL)
Check buttons and Radio buttons
In the image below, the top line shows a check button and the bottom line shows a radio button.
Check buttons
The code for the above check button is:
show_totals = IntVar() check = Checkbutton(text='Show totals', var=show_totals)
The one thing to note here is that we have to tie the check button to a variable, and it can't be just any variable, it has to be a special kind of Tkinter variable, called an IntVar. This variable, show_totals, will be 0 when the check button is unchecked and 1 when it is checked. To access the value of the variable, you need to use its get method, like this:
show_totals.get()
You can also set the value of the variable using its set method. This will automatically check or uncheck the check button on the screen. For instance, if you want the above check button checked at the start of the program, do the following:
show_totals = IntVar() show_totals.set(1) check = Checkbutton(text='Show totals', var=show_totals)
Radio buttons
Radio buttons work similarly. The code for the radio buttons shown at the start of the section is:
color = IntVar() redbutton = Radiobutton(text='Red', var=color, value=1) greenbutton = Radiobutton(text='Green', var=color, value=2) bluebutton = Radiobutton(text='Blue', var=color, value=3)
The value of the IntVar object color will be 1, 2, or 3, depending on whether the left, middle, or right button is selected. These values are controlled by the value option, specified when we create the radio buttons.
Commands
Both check buttons and radio buttons have a command option, where you can set a callback function to run whenever the button is selected or unselected.
Text widget
The Text widget is a bigger, more powerful version of the Entry widget. Here is an example of creating one:
textbox = Text(font=('Verdana', 16), height=6, width=40)
The widget will be 40 characters wide and 6 rows tall. You can still type past the sixth row; the widget will just display only six rows at a time, and you can use the arrow keys to scroll.
If you want a scrollbar associated with the text box you can use the ScrolledText widget. Other than the scrollbar, ScrolledText works more or less the same as Text. An example is of what it looks like is shown below. To use the ScrolledText widget, you will need the following import:
from tkinter.scrolledtext import ScrolledText
Here are a few common commands:
| Statement | Description |
|---|---|
textbox.get(1.0,END) | returns the contents of the text box |
textbox.delete(1.0,END) | deletes everything in the text box |
textbox.insert(END, 'Hello') | inserts text at the end of the text box |
One nice option when declaring the Text widget is undo=True, which allows Ctrl+Z and Ctrl+Y to undo and redo edits. There are a ton of other things you can do with the Text widget. It is almost like a miniature word processor.
Scale widget
A Scale is a widget that you can slide back and forth to select different values. An example is shown below, followed by the code that creates it.
scale = Scale(from_=1, to_=100, length=300, orient='horizontal')
Here are some of the useful options of the Scale widget:
| Option | Description |
|---|---|
from_ | minimum value possible by dragging the scale |
to_ | maximum value possible by dragging the scale |
length | how many pixels long the scale is |
label | specify a label for the scale |
showvalue='NO' | gets rid of the number that displays above the scale |
tickinterval=1 | displays tickmarks at every unit (1 can be changed) |
There are several ways for your program to interact with the scale. One way is to link it with an IntVar just like with check buttons and radio buttons, using the variable option. Another option is to use the scale's get and set methods. A third way is to use the command option, which works just like with buttons.
GUI Events
Often we will want our programs to do something if the user presses a certain key, drags something on a canvas, uses the mouse wheel, etc. These things are called events.
A simple example
The first GUI program we looked at back in this section was a simple temperature converter. Anytime we wanted to convert a temperature we would type in the temperature in the entry box and click the Calculate button. It would be nice if the user could just press the enter key after they type the temperature instead of having to click to Calculate button. We can accomplish this by adding one line to the program:
entry.bind('<Return>', lambda dummy=0:calculate())
This line should go right after you declare the entry box. What it does is it takes the event that the enter (return) key is pressed and binds it to the calculate function.
Well, sort of. The function you bind the event to is supposed to be able to receive a copy of an Event object, but the calculate function that we had previously written takes no arguments. Rather than rewrite the function, the line above uses lambda trick to essentially throw away the Event object.
Common events
Here is a list of some common events:
| Event | Description |
|---|---|
<Button-1> | The left mouse button is clicked. |
<Double-Button-1> | The left mouse button is double-clicked. |
<Button-Release-1> | The left mouse button is released. |
<B1-Motion> | A click-and-drag with the left mouse button. |
<MouseWheel> | The mouse wheel is moved. |
<Motion> | The mouse is moved. |
<Enter> | The mouse is now over the widget. |
<Leave> | The mouse has now left the widget. |
<Key> | A key is pressed. |
| The key name key is pressed. |
For all of the mouse button examples, the number 1 can be replaced with other numbers. Button 2 is the middle button and button 3 is the right button.
The most useful attributes in the Event object are:
| Attribute | Description |
|---|---|
keysym | The name of the key that was pressed |
x, y | The coordinates of the mouse pointer |
delta | The value of the mouse wheel |
Key events
For key events, you can either have specific callbacks for different keys or catch all keypresses and deal with them in the same callback. Here is an example of the latter:
from tkinter import *
def callback(event):
print(event.keysym)
root = Tk()
root.bind('<Key>', callback)
mainloop()
The above program prints out the names of the keys that were pressed. You can use those names in if statements to handle several different keypresses in the callback function, like below:
if event.keysym == 'percent':
# percent (shift+5) was pressed, do something about it...
elif event.keysym == 'a':
# lowercase a was pressed, do something about it...
Use the single callback method if you are catching a lot of keypresses and are doing something similar with all of them. On the other hand, if you just want to catch a couple of specific keypresses or if certain keys have very long and specific callbacks, you can catch keypresses separately like below:
from tkinter import *
def callback1(event):
print('You pressed the enter key.')
def callback2(event):
print('You pressed the up arrow.')
root = Tk()
root.bind('<Return>', callback1)
root.bind('<Up>', callback2)
mainloop()
The key names are the same as the names stored in the keysym attribute. You can use the program from earlier in this section to find the names of all the keys. Here are the names for a few common keys:
| Tkinter name | Common name |
|---|---|
<Return> | Enter key |
<Tab> | Tab key |
<Space> | Spacebar |
<F1>, …, <F12> | F1, …, F12 |
<Next>, <Prior> | Page up, Page down |
<Up>, <Down>, <Left>, <Right> | Arrow keys |
<Home>, <End> | Home, End |
<Insert>, <Delete> | Insert, Delete |
<Caps_Lock>, <Num_Lock> | Caps lock, Number lock |
<Control_L>, <Control_R> | Left and right Control keys |
<Alt_L>, <Alt_R> | Left and right Alt keys |
<Shift_L>, <Shift_R> | Left and right Shift keys |
Most printable keys can be captured with their names, like below:
root.bind('a', callback)
root.bind('A', callback)
root.bind('-', callback)
The exceptions are the spacebar (<Space>) and the less than sign (<Less>). You can also catch key combinations, such as <Shift-F5>, <Control-Next>, <Alt-2>, or <Control-Shift-F1>.
Note
These examples all bind keypresses toroot, which is our name for the main window. You can also bind keypresses to specific widgets. For instance, if you only want the left arrow key to work on a Canvas called canvas, you could use the following:
canvas.bind(<Left>, callback)
One trick here, though, is that the canvas won't recognize the keypress unless it has the GUI's focus. This can be done as below:
canvas.focus_set()
Event examples
Example 1
Here is an example where the user can move a rectangle with the left or right arrow keys.
from tkinter import *
def callback(event):
global move
if event.keysym=='Right':
move += 1
elif event.keysym=='Left':
move -=1
canvas.coords(rect,50+move,50,100+move,100)
root = Tk()
root.bind('<Key>', callback)
canvas = Canvas(width=200,height=200)
canvas.grid(row=0,column=0)
rect = canvas.create_rectangle(50,50,100,100,fill='blue')
move = 0
mainloop()
Example 2
Here is an example program demonstrating mouse events. The program starts by drawing a rectangle to the screen. The user can do the following:
- Drag the rectangle with the mouse (
<B1_Motion>). - Resize the rectangle with the mouse wheel (
<MouseWheel>). - Whenever the user left-clicks, the rectangle will change colors (
<Button-1>). - Anytime the mouse is moved, the current coordinates of the mouse are displayed in a label (
<Motion>).
Here is the code for the program:
from tkinter import *
def mouse_motion_event(event):
label.configure(text='({}, {})'.format(event.x, event.y))
def wheel_event(event):
global x1, x2, y1, y2
if event.delta>0:
diff = 1
elif event.delta<0:
diff = -1
x1+=diff
x2-=diff
y1+=diff
y2-=diff
canvas.coords(rect,x1,y1,x2,y2)
def b1_event(event):
global color
if not b1_drag:
color = 'Red' if color=='Blue' else 'Blue'
canvas.itemconfigure(rect, fill=color)
def b1_motion_event(event):
global b1_drag, x1, x2, y1, y2, mouse_x, mouse_y
x = event.x
y = event.y
if not b1_drag:
mouse_x = x
mouse_y = y
b1_drag = True
return
x1+=(x-mouse_x)
x2+=(x-mouse_x)
y1+=(y-mouse_y)
y2+=(y-mouse_y)
canvas.coords(rect,x1,y1,x2,y2)
mouse_x = x
mouse_y = y
def b1_release_event(event):
global b1_drag
b1_drag = False
root=Tk()
label = Label()
canvas = Canvas(width=200, height=200)
canvas.bind('<Motion>', mouse_motion_event)
canvas.bind('<ButtonPress-1>', b1_event)
canvas.bind('<B1-Motion>', b1_motion_event)
canvas.bind('<ButtonRelease-1>', b1_release_event)
canvas.bind('<MouseWheel>', wheel_event)
canvas.focus_set()
canvas.grid(row=0, column=0)
label.grid(row=1, column=0)
mouse_x = 0
mouse_y = 0
b1_drag = False
x1 = y1 = 50
x2 = y2 = 100
color = 'blue'
rect = canvas.create_rectangle(x1,y1,x2,y2,fill=color)
mainloop()

Here are a few notes about how the program works:
- First, every time the mouse is moved over the canvas, the
mouse_motion_eventfunction is called. This function prints the mouse's current coordinates which are contained in theEventattributesxandy. - The
wheel_eventfunction is called whenever the user uses the mouse (scrolling) wheel. TheEventattributedeltacontains information about how quickly and in what direction the wheel was moved. We just stretch or shrink the rectangle based on whether the wheel was moved forward or backward. - The
b1_eventfunction is called whenever the user presses the left mouse button. The function changes the color of the rectangle whenever the rectangle is clicked. There is a global variable here calledb1_dragthat is important. It is set toTruewhenever the user is dragging the rectangle. When dragging is going on, the left mouse button is down and theb1_eventfunction is continuously being called. We don't want to keep changing the color of the rectangle in that case, hence the if statement. - The dragging is accomplished mostly in the
b1_motion_eventfunction, which is called whenever the left mouse button is down and the mouse is being moved. It uses global variables that keep track of what the mouse's position was the last time the function was called, and then moves the rectangle according to the difference between the new and old position. When the dragging is down, the left mouse button will be released. When that happens, theb1_release_eventfunction is called, and we set the globalb1_dragvariable accordingly. - The
focus_setmethod is needed because the canvas will not recognize the mouse wheel events unless the focus is on the canvas. - One problem with this program is that the user can modify the rectangle by clicking anywhere on the canvas, not just on rectangle itself. If we only want the changes to happen when the mouse is over the rectangle, we could specifically bind the rectangle instead of the whole canvas, like below:
canvas.tag_bind(rect, '<B1-Motion>', b1_motion_event)
- Finally, the use of global variables here is a little messy. If this were part of a larger project, it might make sense to wrap all of this up into a class.
GUI Programming III
This chapter contains a few more GUI odds and ends.
Title bar
The GUI window that Tkinter creates says Tk by default. Here is how to change it:
root.title('Your title')
Disabling things
Sometimes you want to disable a button so it can't be clicked. Buttons have an attribute state that allows you to disable the widget. Use state=DISABLED to disable the button and state=NORMAL to enable it. Here is an example that creates a button that starts out disabled and then enables it:
button = Button(text='Hi', state=DISABLED, command=function) button.configure(state=NORMAL)
You can use the state attribute to disable many other types of widgets, too.
Getting the state of a widget
Sometimes, you need to know things about a widget, like exactly what text is in it or what its background color is. The cget method is used for this. For example, the following gets the text of a label called label:
label.cget('text')
This can be used with buttons, canvases, etc., and it can be used with any of their properties, like bg, fg, state, etc. As a shortcut, Tkinter overrides the [] operators, so that label['text'] accomplishes the same thing as the example above.
Message boxes
Message boxes are windows that pop up to ask you a question or say something and then go away. To use them, we need an import statement:
from tkinter.messagebox import *
There are a variety of different types of message boxes. For each of them you can specify the message the user will see as well as the title of the message box. Here are three types of message boxes, followed by the code that generates them:
showinfo(title='Message for you', message='Hi There!') askquestion(title='Quit?', message='Do you really want to quit?') showwarning(title='Warning', message='Unsupported format')
Below is a list of all the types of message boxes. Each displays a message in its own way.
| Message Box | Special properties |
|---|---|
showinfo | OK button |
askokcancel | OK and Cancel buttons |
askquestion | Yes and No buttons |
askretrycancel | Retry and a Cancel buttons |
askyesnocancel | Yes, No, and Cancel buttons |
showerror | An error icon and an OK button |
showwarning | A warning icon and an OK button |
Each of these functions returns a value indicating what the user clicked. See the next section for a simple example of using the return value. Here is a table of the return values:
| Function | Return value (based on what user clicks) |
|---|---|
showinfo | Always returns 'ok' |
askokcancel | OK—True Cancel or window closed—False |
askquestion | Yes—'yes' No—'no' |
askretrycancel | Retry—True Cancel or window closed—False |
askyesnocancel | Yes—True No—False anything else—None |
showerror | Always returns 'ok' |
showwarning | Always returns 'ok' |
Destroying things
To get rid of a widget, use its destroy method. For instance, to get rid of a button called button, do the following:
button.destroy()
To get rid of the entire GUI window, use the following:
root.destroy()
Stopping a window from being closed
When your user tries to close the main window, you may want to do something, like ask them if they really want to quit. Here is a way to do that:
from tkinter import *
from tkinter.messagebox import askquestion
def quitter_function():
answer = askquestion(title='Quit?', message='Really quit?')
if answer=='yes':
root.destroy()
root = Tk()
root.protocol('WM_DELETE_WINDOW', quitter_function)
mainloop()
The key is the following line, which cause quitter_function to be called whenever the user tries to close the window.
root.protocol('WM_DELETE_WINDOW', quitter_function)
Updating
Tkinter updates the screen every so often, but sometimes that is not often enough. For instance, in a function triggered by a button press, Tkinter will not update the screen until the function is done. If, in that function, you want to change something on the screen, pause for a short while, and then change something else, you will need to tell Tkinter to update the screen before the pause. To do that, just use this:
root.update()
If you only want to update a certain widget, and nothing else, you can use the update method of that widget. For example,
canvas.update()
A related thing that is occasionally useful is to have something happen after a scheduled time interval. For instance, you might have a timer in your program. For this, you can use the after method. Its first argument is the time in milliseconds to wait before updating and the second argument is the function to call when the time is right. Here is an example that implements a timer:
from time import time
from tkinter import *
def update_timer():
time_left = int(90 - (time()-start))
minutes = time_left // 60
seconds = time_left % 60
time_label.configure(text='{}:{:02d}'.format(minutes, seconds))
root.after(100, update_timer)
root = Tk()
time_label = Label()
time_label.grid(row=0, column=0)
start = time()
update_timer()
mainloop()
This example uses the time module, which is covered in this section.
Dialogs
Many programs have dialog boxes that allow the user to pick a file to open or to save a file. To use them in Tkinter, we need the following import statement:
from tkinter.filedialog import *
Tkinter dialogs usually look like the ones that are native to the operating system.
Here are the most useful dialogs:
| Dialog | Description |
|---|---|
askopenfilename | Opens a typical file chooser dialog |
askopenfilenames | Like previous, but user can pick more than one file |
asksaveasfilename | Opens a typical file save dialog |
askdirectory | Opens a directory chooser dialog |
The return value of askopenfilename and asksaveasfilename is the name of the file selected. There is no return value if the user does not pick a value. The return value of askopenfilenames is a list of files, which is empty if no files are selected. The askdirectory function returns the name of the directory chosen.
There are some options you can pass to these functions. You can set initialdir to the directory you want the dialog to start in. You can also specify the file types. Here is an example:
filename=askopenfilename(initialdir='c:\\python31\\',
filetypes=[('Image files', '.jpg .png .gif'),
('All files', '*')])
A short example
Here is an example that opens a file dialog that allows you to select a text file. The program then displays the contents of the file in a textbox.
from tkinter import *
from tkinter.filedialog import *
from tkinter.scrolledtext import ScrolledText
root = Tk()
textbox = ScrolledText()
textbox.grid()
filename=askopenfilename(initialdir='c:\\python31\\',
filetypes=[('Text files', '.txt'),
('All files', '*')])
s = open(filename).read()
textbox.insert(1.0, s)
mainloop()
Menu bars
We can create a menu bar, like the one below, across the top of a window.
Here is an example that uses some of the dialogs from the previous section:
from tkinter import *
from tkinter.filedialog import *
def open_callback():
filename = askopenfilename()
# add code here to do something with filename
def saveas_callback():
filename = asksaveasfilename()
# add code here to do something with filename
root = Tk()
menu = Menu()
root.config(menu=menu)
file_menu = Menu(menu, tearoff=0)
file_menu.add_command(label='Open', command=open_callback)
file_menu.add_command(label='Save as', command=saveas_callback)
file_menu.add_separator()
file_menu.add_command(label='Exit', command=root.destroy)
menu.add_cascade(label='File', menu=file_menu)
mainloop()
New windows
Creating a new window is easy. Use the Toplevel function:
window = Toplevel()
You can add widgets to the new window. The first argument when you create the widget needs to be the name of the window, like below
new_window = Toplevel() label = Label(new_window, text='Hi') label.grid(row=0, column=0)
pack
There is an alternative to grid called pack. It is not as versatile as grid, but there are some places where it is useful. It uses an argument called side, which allows you to specify four locations for your widgets: TOP, BOTTOM, LEFT, and RIGHT. There are two useful optional arguments, fill and expand. Here is an example.
button1=Button(text='Hi') button1.pack(side=TOP, fill=X) button2=Button(text='Hi') button2.pack(side=BOTTOM)
The fill option causes the widget to fill up the available space given to it. It can be either X, Y or BOTH. The expand option is used to allow the widget to expand when its window is resized. To enable it, use expand=YES.
Note
You can use pack for some frames, and grid for others; just don't mix pack and grid within the same frame, or Tkinter won't know quite what to do.
StringVar
In this section we saw how to tie a Tkinter variable, called an IntVar, to a check button or a radio button. Tkinter has another type of variable called a StringVar that holds strings. This type of variable can be used to change the text in a label or a button or in some other widgets. We already know how to change text using the configure method, and a StringVar provides another way to do it.
To tie a widget to a StringVar, use the textvariable option of the widget. A StringVar has get and set methods, just like an IntVar, and whenever you set the variable, any widgets that are tied to it are automatically updated.
Here is a simple example that ties two labels to the same StringVar. There is also a button that when clicked will alternate the value of the StringVar (and hence the text in the labels).
from tkinter import *
def callback():
global count
s.set('Goodbye' if count%2==0 else 'Hello')
count +=1
root = Tk()
count = 0
s = StringVar()
s.set('Hello')
label1 = Label(textvariable = s, width=10)
label2 = Label(textvariable = s, width=10)
button = Button(text = 'Click me', command = callback)
label1.grid(row=0, column=0)
label2.grid(row=0, column=1)
button.grid(row=1, column=0)
mainloop()
More with GUIs
We have left out quite a lot about Tkinter. See Lundh's Introduction to Tkinter for more. Tkinter is versatile and simple to work with, but if you need something more powerful, there are other third-party GUIs for Python.
Further Graphical Programming
Python 2 vs Python 3
As of this writing, the most recent version of Python is 3.2, and all the code in this book is designed to run in Python 3.2. The tricky thing is that as of version 3.0, Python broke compatibility with older versions of Python. Code written in those older versions will not always work in Python 3. The problem with this is there were a number of useful libraries written for Python 2 that, as of this writing, have not yet been ported to Python 3. We want to use these libraries, so we will have to learn a little about Python 2. Fortunately, there are only a few big differences that we have to worry about.
Division
The division operator, /, in Python 2, when used with integers, behaves like //. For instance, 5/4 in Python 2 evaluates to 1, whereas 5/4 in Python 3 evaluates to 1.2. This is the way the division operator behaves in a number of other programming languages. In Python 3, the decision was made to make the division operator behave the way we are used from math.
In Python 2, if you want to get 1.25 by dividing 5 and 4, you need to do 5/4.0. At least one of the arguments has to be a float in order for the result to be a float. If you are dividing two variables, then instead of x/y, you may need to do x/float(y).
print
The print function in Python 3 was actually the print statement in Python 2. So in Python 2, you would write
print 'Hello'
without any parentheses. This code will no longer work in Python 3 because the print statement is now the print function, and functions need parentheses. Also, the current print function has those useful optional arguments, sep and end, that are not available in Python 2.
input
The Python 2 equivalent of the input function is raw_input.
range
The range function can be inefficient with very large ranges in Python 2. The reason is that in Python 2, if you use range(10000000), Python will create a list of 10 million numbers. The range statement in Python 3 is more efficient and instead of generating all 10 million things at once, it only generates the numbers as it needs them. The Python 2 function that acts like the Python 3 range is xrange.
String formatting
String formatting in Python 2 is a little different than in Python 3. When using the formatting codes inside curly braces, in Python 2, you need to specify an argument number. Compare the examples below:
Python 2: 'x={0:3d}, y={1:3d}, z={2:3d}'.format(x,y,z)
Python 3: 'x={:3d}, y={:3d}, z={:3d}'.format(x,y,z)
As of Python 3.1, specifying the argument numbers was made optional.
There is also an older style of formatting that you may see from time to time that uses the % operator. An example is shown below along with the corresponding new style.
Python 2: 'x=%3d, y=%6.2f, z=%3s' % (x,y,z)
Python 3: 'x={:3d}, y={:6.2f}, z={:3s}'.format(x,y,z)
Module names
Some modules were renamed and reorganized. Here are a few Tkinter name changes:
| Python 2 | Python 3 |
|---|---|
| Tkinter | tkinter |
| ScrolledText | tkinter.scrolledtext |
| tkMessageBox | tkinter.messagebox |
| tkFileDialog | tkinter.filedialog |
There are a number of other modules we'll see later that were renamed, mostly just changed to lowercase. For instance, Queue in Python 2 is now queue in Python 3.
Dictionary comprehensions
Dictionary comprehensions are not present in Python 2.
Other changes
There are quite a few other changes in the language, but most of them are with features more advanced than we consider here.
Importing future behavior
The following import allows us to use Python 3's division behavior in Python 2.
from __future__ import division
There are many other things you can import from the future.
The Python Imaging Library
The Python Imaging Library (PIL) contains useful tools for working with images. As of this writing, the PIL is only available for Python 2.7 or earlier. The PIL is not part of the standard Python distribution, so you'll have to download and install it separately. It's easy to install, though.
PIL hasn't been maintained since 2009, but there is a project called Pillow that it nearly compatible with PIL and works in Python 3.0 and later.
We will cover just a few features of the PIL here. A good reference is The Python Imaging Library Handbook.
Using images other than GIFs with Tkinter
Tkinter, as we've seen, can't use JPEGs and PNGs. But it can if we use it in conjunction with the PIL. Here is a simple example:
from Tkinter import *
from PIL import Image, ImageTk
root = Tk()
cheetah_image = ImageTk.PhotoImage(Image.open('cheetah.jpg'))
button = Button(image=cheetah_image)
button.grid(row=0, column=0)
mainloop()
The first line imports Tkinter. Remember that in Python 2 it's an uppercase Tkinter. The next line imports a few things from the PIL. Next, where we would have used Tkinter's PhotoImage to load an image, we instead use a combination of two PIL functions. We can then use the image like normal in our widgets.
Images
PIL is the Python Imaging Library, and so it contains a lot of facilities for working with images. We will just show a simple example here. The program below displays a photo on a canvas and when the user clicks a button, the image is converted to grayscale.
from Tkinter import *
from PIL import Image, ImageTk
def change():
global image, photo
pix = image.load()
for i in range(photo.width()):
for j in range(photo.height()):
red,green,blue = pix[i,j]
avg = (red+green+blue)//3
pix[i,j] = (avg, avg, avg)
photo=ImageTk.PhotoImage(image)
canvas.create_image(0,0,image=photo,anchor=NW)
def load_file(filename):
global image, photo
image=Image.open(filename).convert('RGB')
photo=ImageTk.PhotoImage(image)
canvas.configure(width=photo.width(), height=photo.height())
canvas.create_image(0,0,image=photo,anchor=NW)
root.title(filename)
root = Tk()
button = Button(text='Change', font=('Verdana', 18), command=change)
canvas = Canvas()
canvas.grid(row=0)
button.grid(row=1)
load_file('pic.jpg')
mainloop()
Let's first look at the load_file function. Many of the image utilities are in the Image module. We give a name, image, to the object created by the Image.open statement. We also use the convert method to convert the image into RGB (Red-Green-Blue) format. We will see why in a minute. The next line creates an ImageTk object called photo that gets drawn to the Tkinter canvas. The photo object has methods that allow us to get its width and height so we can size the canvas appropriately.
Now look at the change function. The image object has a method called load that gives access to the individual pixels that make up the image. This returns a two-dimensional array of RGB values. For instance, if the pixel in the upper left corner of the image is pure white, then pix[0,0] will be (255,255,255). If the next pixel to the right is pure black, pix[1,0] will be (0,0,0). To convert the image to grayscale, for each pixel we take the average of its red, green, and blue components, and reset the red, green, and blue components to all equal that average. Remember that if the red, green, and blue are all the same, then the color is a shade of gray. After modifying all the pixels, we create a new ImageTk object from the modified pixel data and display it on the canvas.
You can have a lot of fun with this. Try modifying the change function. For instance, if we use the following line in the change function, we get an effect that looks like a photo negative:
pix[i,j] = (255-red, 255-green, 255-blue)
Try seeing what interesting effects you can come up with.
Note, though, that this way of manipulating images is the slow, manual way. PIL has a number of much faster functions for modifying images. You can very easily change the brightness, hue, and contrast of images, resize them, rotate them, and much more. See the PIL reference materials for more on this.
putdata
If you are interested drawing mathematical objects like fractals, plotting points pixel-by-pixel can be very slow in Python. One way to speed things up is to use the putdata method. The way it works is you supply it with a list of RGB pixel values, and it will copy it into your image. Here is a program that plots a 300 ×300 grid of random colors.
from random import randint
from Tkinter import *
from PIL import Image, ImageTk
root = Tk()
canvas = Canvas(width=300, height=300)
canvas.grid()
image=Image.new(mode='RGB',size=(300,300))
L = [(randint(0,255), randint(0,255), randint(0,255))
for x in range(300) for y in range(300)]
image.putdata(L)
photo=ImageTk.PhotoImage(image)
canvas.create_image(0,0,image=photo,anchor=NW)
mainloop()
(Left) putdata example (Right) ImageDraw example
ImageDraw
The ImageDraw module gives another way to draw onto images. It can be used to draw rectangles, circles, points, and more, just like Tkinter canvases, but it is faster. Here is a short example that fills the image with a dark blue color and then 100 randomly distributed yellow points.
from random import randint from Tkinter import * from PIL import Image, ImageTk, ImageDraw root = Tk() canvas = Canvas(width=300, height=300) canvas.grid() image=Image.new(mode='RGB',size=(300,300)) draw = ImageDraw.Draw(image) draw.rectangle([(0,0),(300, 300)],fill='#000030') L = [(randint(0,299), randint(0, 299)) for i in range(100)] draw.point(L, fill='yellow') photo=ImageTk.PhotoImage(image) canvas.create_image(0,0,image=photo,anchor=NW) mainloop()
To use ImageDraw, we have to first create an ImageDraw object and tie it to the Image object. The draw.rectangle method works similarly to the create_rectangle method of canvases, except for a few differences with parentheses. The draw.point method is used to plot individual pixels. A nice feature of it is we can pass a list of points instead of having to plot each thing in the list separately. Passing a list is also much faster.
Pygame
Pygame is a library for creating two-dimensional games in Python. It can be used to can make games at the level of old arcade or Nintendo games. It can be downloaded and easily installed from here. There are a number of tutorials there to help you get started. I don't know a whole lot about Pygame, so I won't cover it here, though perhaps in a later edition I will.
PART III: INTERMEDIATE TOPICS
Miscellaneous topics III
In this chapter we examine a variety of useful topics.
Mutability and References
If L is a list and s is a string, then L[0] gives the first element of the list and s[0] the first element of the string. If we want to change the first element of the list to 3, L[0]=3 will do it. But we cannot change a string this way. The reason has to do with how Python treats lists and strings. Lists (and dictionaries) are said to be mutable, which means their contents can change. Strings, on the other hand, are immutable, which means they cannot be changed. The reason strings are immutable is partly for performance (immutable objects are faster) and partly because strings are thought of fundamental in the same way that numbers are. It makes some other aspects of the language easier as well.
Making copies
Another place that lists and strings differ is when we try to make copies. Consider the following code:
s = 'Hello'
copy = s
s = s + '!!!'
print('s is now:', s, ' Copy:', copy)
s is now: Hello!!! Copy: Hello
In the code above we make a copy of s and then change s. Everything works as we would intuitively expect. Now look at similar code with lists:
L = [1,2,3]
copy = L
L[0]=9
print('L is now:', L, ' Copy:', copy)
L is now: [9, 2, 3] Copy: [9, 2, 3]
We can see that the list code did not work as we might have expected. When we changed L, the copy got changed as well. As mentioned in this section, the proper way to make a copy of L is copy=L[:]. The key to understanding these examples is references.
References
Everything in Python is an object. This includes numbers, strings, and lists. When we do a simple variable assignment, like x=487, what actually happens is Python creates an integer object with the value 487, and the variable x acts as a reference to that object. It's not that the value 4 is stored in a memory location named x, but rather that 487 is stored somewhere in memory, and x points to that location. If we come along and declare y=487, then y also points to that same memory location.
On the other hand, if we then come along and say x=721, what happens is we create a new integer object with value 721 somewhere in memory and x now points at that. The 487 still exists in memory where it was and it will stay there at least until there is nothing left pointing at it, at which point its memory location will be free to use for something else.
All objects are treated the same way. When we set s='Hello', the string object Hello is somewhere in memory and s is a reference to it. When we then say copy=x, we are actually saying that copy is another reference to 'Hello'. If we then do s=s+'!!!', what happens is a new object 'Hello!!!' is created and because we assigned s to it, s is now a reference to that new object, 'Hello!!!'. Remember that strings are immutable, so there is no changing 'Hello' into something. Rather, Python creates a new object and points the variable s to it.
When we set L=[1,2,3], we create a list object [1,2,3] and a reference, L, to it. When we say copy=L, we are making another reference to the object [1,2,3]. When we do L[0]=9, because lists are mutable, the list [1,2,3] is changed, in place, to [9,2,3]. No new object is created. The list [1,2,3] is now gone, and since copy is still pointing to the same location, it's value is [9,2,3].
On the other hand, if we instead use copy=L[:], we are actually creating a new list object somewhere else in memory so that there are two copies of [1,2,3] in memory. Then when we do L[0]=9, we are only changing the thing that L points to, and copy still points to [1,2,3].
Just one further note to drive the point home. If we set x=487 and then set x=721, we are first creating an integer object 487 and pointing x to it. When we then set x=721, we are creating a new integer object 721 and pointing x to it. The net effect is that it seems like the “value” of x is changing, but what is in fact changing is what x is pointing to.
Garbage collection
Internally Python maintains a count of how many references there are to each object. When the reference count of an object drops to 0, then the object is no longer needed, and the memory it had been using becomes available again.
Tuples
A tuple is essentially an immutable list. Below is a list with three elements and a tuple with three elements:
L = [1,2,3] t = (1,2,3)
Tuples are enclosed in parentheses, though the parentheses are actually optional. Indexing and slicing work the same as with lists. As with lists, you can get the length of the tuple by using the len function, and, like lists, tuples have count and index methods. However, since a tuple is immutable, it does not have any of the other methods that lists have, like sort or reverse, as those change the list.
We have seen tuples in a few places already. For instance, fonts in Tkinter are specified as pairs, like ('Verdana', 14), and sometimes as triples. The dictionary method items returns a list of tuples. Also, when we use the following shortcut for exchanging the value of two or more variables, we are actually using tuples:
a,b = b,a
One reason why there are both lists and tuples is that in some situations, you might want an immutable type of list. For instance, lists cannot serve as keys in dictionaries because the values of lists can change and it would be a nightmare for Python dictionaries to have to keep track of. Tuples, however, can serve as keys in dictionaries. Here is an example assigning grades to teams of students:
grades = {('John', 'Ann'): 95, ('Mike', 'Tazz'): 87}
Also, in situations where speed really matters, tuples are generally faster than lists. The flexibility of lists comes with a corresponding cost in speed.
tuple
To convert an object into a tuple, use tuple. The following example converts a list and a string into tuples:
t1 = tuple([1,2,3])
t2 = tuple('abcde')
Note
The empty tuple is (). The way to get a tuple with one element is like this: (1,). Something like (1) will not work because that just evaluates to 1 as in an ordinary calculation. For instance, in the expression 2+(3*4), we don't want the (3*4) to be a tuple, we want it to evaluate to a number.
Sets
Python has a data type called a set. Sets work like mathematical sets. They are a lot like lists with no repeats. Sets are denoted by curly braces, like below:
S = {1,2,3,4,5}
Recall that curly braces are also used to denote dictionaries, and {} is the empty dictionary. To get the empty set, use the set function with no arguments, like this:
S = set()
This set function can also be used to convert things to sets. Here are two examples:
set([1,4,4,4,5,1,2,1,3])
set('this is a test')
{1, 2, 3, 4, 5}
{'a', ' ', 'e', 'i', 'h', 's', 't'}
Notice that Python will store the data in a set in whatever order it wants to, not necessarily the order you specify. It's the data in the set that matters, not the order of the data. This means that indexing has no meaning for sets. You can't do s[0], for instance.
Working with sets
There are a few operators that work with sets.
| Operator | Description | Example |
|---|---|---|
+ | union | {1,2,3} + {3,4} → {1,2,3,4} |
& | intersection | {1,2,3} & {3,4} → {3} |
- | difference | {1,2,3} - {3,4} → {1,2} |
^ | symmetric difference | {1,2,3} ^ {3,4} → {1,2,4} |
in | is an element of | 3 in {1,2,3} → True |
| Method | Description |
|---|---|
S.add(x) | Add x to the set |
S.remove(x) | Remove x from the set |
S.issubset(A) | Returns True if S ⊂ A and False otherwise. |
S.issuperset(A) | Returns True if A ⊂ S and False otherwise. |
Finally, we can do set comprehensions just like list comprehensions:
s = {i**2 for i in range(12)}
{0, 1, 4, 100, 81, 64, 9, 16, 49, 121, 25, 36}
Set comprehensions are not present in Python 2.
Example: removing repeated elements from lists
We can use the fact that a set can have no repeats to remove all repeats from a list. Here is an example:
L = [1,4,4,4,5,1,2,1,3] L = list(set(L))
After this, L will equal [1,2,3,4,5].
Example: wordplay
Here is an example of an if statement that uses a set to see if every letter in a word is either an a, b, c, d, or e:
if set(word).containedin('abcde'):
Unicode
It used to be computers could only display 255 different characters, called ASCII characters. In this system, characters are allotted one byte of memory each, which gives 255 possible characters, each with a corresponding numerical value. Characters 0 through 31 include various control characters, including '\n' and '\t'. After that came some special symbols, then numbers, capital letters, lowercase letters, and a few more symbols. Beyond that are a variety of other symbols, including some international characters.
However, 255 characters is not nearly enough to represent all of the symbols used throughout the alphabets of the world. The new standard is Unicode, which uses more than one byte to store character data. Unicode currently supports over 65,000 characters. “Standard” isn't quite the right word here, as there are actually several standards in use, and this can cause some trouble. If you need to work with unicode data, do some research into it first to learn about all the craziness.
In Unicode, characters still have numerical equivalents. If you would like to go back and forth between a character and its numerical equivalent, use the chr and ord built-in functions. For example, use ord('A') to get the numerical value of 'A', and use chr(65) to get the character with numerical value 65. Here is a short example that prints out the first 1000 Unicode characters.
print('';.join([chr(i) for i in range(1000)]))

Python supports Unicode, both in strings and in the names of variables, functions, etc. There are some differences between Python 2 and Python 3 in support for Unicode.
sorted
First a definition: an iterable is an object that allows you to loop through its contents. Iterables include lists, tuples, strings, and dictionaries. There are a number of Python methods that work on any iterable.
The sorted function is a built-in function that can be used to sort an iterable. As a first example, we can use it to sort a list. Say L=[3,1,2]. The following sets M to [1,2,3].
M = sorted(L)
The difference between sorted and L.sort is that L.sort() changes the original list L, but sorted(L) does not.
The sorted function can be used on other iterables. The result is a sorted list. For instance, sorted('xyzab') returns the list ['a','b','x','y','z']. If we really want the result to be a string, we can use the join method:
s = '';.join(sorted('xyzab'))
This sets s to 'abxyz'.
Using sorted on a dictionary sorts the keys.
if-else operator
This is a convenient operator that can be used to combine an if/else statement into a single line. Here is an example:
x = 'a' if y==4 else 'b'
This is equivalent to
if y==4:
x='a'
else:
x='b'
Here is another example along with two sample outputs:
print('He scored ', score, ' point', 's.' if score>1 else '.', sep='';)
He scored 5 points. He scored 1 point.
continue
The continue statement is a cousin of the break statement for loops. When a continue statement is encountered in a for loop, the program ignores all the code in the loop beyond the continue statement and jumps back up to the start of the loop, advancing the loop counter as necessary. Here is an example. The code on the right accomplishes the same thing as the code on the left.
for s in L: for s in L:
if s not in found: if s in found: continue
count+=1 count+=1
if s[0]=='a': if s[0]=='a':
count2+=1 count2+=1
The continue statement is something you can certainly do without, but you may see it from time to time and it occasionally can make for simpler code.
eval and exec
The eval and exec functions allow a program to execute Python code while the program is running. The eval function is used for simple expressions, while exec can execute arbitrarily long blocks of code.
eval
We have seen eval many times before with input statements. One nice thing about using eval with an input statement is that the user need not just enter a number. They can enter an expression and Python will compute it. For instance, say we have the following:
num = eval(input('Enter a number: '))
The user can enter 3*(4+5) and Python will compute that expression. You can even use variables in the expression.
Here is an example of eval in action.
def countif(L, condition):
return len([i for i in L if eval(condition)])
This behaves like a spreadsheet COUNTIF function. It counts how many items in a list satisfy a certain condition. What eval does for us here is allows the condition to be specified by the user as a string. For instance, countif(L,'i>5') will return how many items in L are greater than 5.
Here is another common spreadsheet function:
def sumif(L, condition):
return sum([i for i in L if eval(condition)])
exec
The exec function takes a string consisting of Python code and executes it. Here is an example:
s = """x=3
for i in range(4):
print(i*x)"""
exec(s)
One nice use of the exec function is to let a program's user define math functions to use while the program is running. Here is the code to do that:
s = input('Enter function: ')
exec('def f(x): return ' + s)
I have used this code in a graph plotting program that allows users to enter equations to be graphed, and I have used it in a program where the user can enter a function and the program will numerically approximate its roots.
You can use exec to have your program generate all sorts of Python code while it is running. This allows your program to essentially modify itself while it is running.
Note
In Python 2 exec is a statement, not a function, so you may see it used without parentheses in older code.
Security issue
The eval and exec functions can be dangerous. There is always the chance that your users might input some code that could do something dangerous to the machine. They could also use it to inspect the values of your variables (which could be bad if, for some reason, you were storing passwords in a variable). So, you will want to be careful about using these functions in code where security is important. One option for getting input without eval is to do something like this:
num = int(input('Enter a number: '))
This assumes num is an integer. Use float or list or whatever is appropriate to the data you are expecting.
enumerate and zip
The built-in enumerate function takes an iterable and returns a new iterable consisting of pairs (i,x) where i is an index and x is the corresponding element from the iterable. For example:
s = 'abcde'
for (i,x) in enumerate(s):
print(i+1, x)
1 a 2 b 3 c 4 d 5 e
The object returned is something that is like a list of pairs, but not exactly. The following will give a list of pairs:
list(enumerate(s))
The for loop above is equivalent to the following:
for i in range(len(s)):
print(i+1, s[i])
The enumerate code can be shorter or clearer in some situations. Here is an example that returns a list of the indices of all the ones in a string:
[j for (j,c) in enumerate(s) if c=='1']
zip
The zip function takes two iterables and “zips” them up into a single iterable that contains pairs (x,y), where x is from the first iterable, and y is from the second. Here is an example:
s = 'abc' L = [10, 20, 30] z = zip(s,L) print(list(z))
[('a',10]), ('b',20), ('c',30)]
Just like with enumerate, the result of zip is not quite a list, but if we do list(zip(s,L)), we can get a list from it.
Here is an example that uses zip to create a dictionary from two lists.
L = ['one', 'two', 'three'] M = [4, 9, 15] d = dict(zip(L,M))
{'three': 15, 'two': 9, 'one': 4}
This technique can be used to create a dictionary while your program is running.
copy
The copy module has a couple of useful methods, copy and deepcopy. The copy method can be used, for instance, to make a copy of an object from a user-defined class. As an example, suppose we have a class called Users and we want to make a copy of a specific user u. We could do the following:
from copy import copy u_copy = copy(u)
But the copy method has certain limitations, as do other copying techniques, like M=L[:] for lists. For example, suppose L = [1,2,3], [4,5,6]]. If we make a copy of this by doing M=L[:], and then set L[0][0]=100, this will affect M[0][0] as well. This is because the copy is only a shallow copy—the references to the sublists that make up L were copied, instead of copies of those sublists. This sort of thing can be a problem anytime we are copying an object that itself consists of other objects.
The deepcopy method is used in this type of situation to only copy the values and not the references. Here is how it would work:
from copy import deepcopy M = deepcopy(L)
More with strings
There are a few more facts about strings that we haven't yet talked about.
translate
The translate method is used to translate strings, character-by-character. The translation is done in two steps. First, use maketrans to create a special kind of dictionary that defines how things will be translated. You specify an ordinary dictionary and it creates a new one that is used in the translation. Then pass that dictionary to the translate method to do the translating. Here is a simple example:
d = str.maketrans({'a':'1', 'b':'2'})
print('abaab'.translate(d))
The result is '12112'.
Here is an example where we use translate to implement a simple substitution cipher. A substitution cipher is a simple way to encrypt a message, where each letter is replaced by a different letter. For instance, maybe every a is replaced by a g, and every b by an x, etc. Here is the code:
from random import shuffle # create the key alphabet = 'abcdefghijklmnopqrstuvwxyz' L = list(alphabet) shuffle(L) # create the encoding and decoding dictionaries encode_dict = str.maketrans(dict(zip(alphabet, L))) decode_dict = str.maketrans(dict(zip(L, alphabet))) # encode and decode 'this is a secret' s = 'this is a secret'.translate(encode_dict) t = s.translate(decode_dict) print(alphabet, '';.join(L), t, s, sep='\n')
abcdefghijklmnopqrstuvwxyz qjdpaztxghuflicornkesyvmwb exgk gk q kadnae this is a secret
The way it works is we first create the encryption key, which says which letter a gets replaced with, b gets replaced with, etc. This is done by shuffling the alphabet. We then create a translation table for both encoding and decoding, using the zip trick of this section for creating dictionaries. Finally, we use the translate method to do the actual substituting.
partition
The partition method is similar to the list split method. The difference is illustrated below:
'3.14159'.partition('.')
'3.14159'.split('.')
('3', '.', '14159')
['3', '14159]
The difference is that the argument to the function is returned as part of the output. The partition method also returns a tuple instead of a list. Here is an example that calculates the derivative a simple monomial entered as a string. The rule for derivatives is that the derivative of axn is naxn-1.
s = input('Enter a monomial: ')
coeff, power = s.partition('x^')
print('{}x^{}'.format(int(coeff)*int(power), int(power)-1)
Enter a monomial: 2x12 24x11
Note
These methods, and many others, could be done directly just using the basic tools of the language like for loops, if statements, etc. The idea, though, is that those things that are commonly done are made into methods or classes that are part of the standard Python distribution. This can help you from having to reinvent the wheel and they can also make your programs more reliable and easier to read.
Comparing strings
Comparison of strings is done alphabetically. For example, the following will print Yes.
if 'that' < 'this':
print('Yes')
Beyond that, if the string contains characters other than letters, the comparison is based off the ord value of the characters.
Miscellaneous tips and tricks
Here are a few useful tips:
Statements on the same line
You can write an if statement and the statement that goes with it on the same line.
if x==3: print('Hello')
You can also combine several statements on a line if you separate them by semicolons. For example:
a=3; b=4; c=5
Don't overuse either of these, as they can make your code harder to read. Sometimes, though, they can make it easier to read.
Calling multiple methods
You can call several methods in a row, like below:
s = open('file.txt').read().upper()
This example reads the contents of a file, then converts everything to uppercase, and stores the result in s. Again, be careful not to overdo it with too many methods in a row or your code may be difficult to read.
None
In addition to int, float, str, list, etc., Python has a data type called None. It basically is the Python version of nothing. It indicates that there is nothing when you might have expected there to be something, such as the return value of a function. You may see it show up here and there.
Documentation strings
When defining a function, you can specify a string that contains information about how the function works. Then anyone who uses the function can use Python's help function to get information about your function. Here an example:
def square(x):
""" Returns x squared. """
return x**2
>>> help(square)
Help on function square in module __main__:
square(x)
Returns x squared.
You can also use documentation strings right after a class statement to provide information about your class.
Running your Python programs on other computers
Your Python programs can be run on other computers that have Python installed. Macs and Linux machines usually have Python installed, though the version may not be up to date with the one you are using, and those machines may not have additional libraries you are using.
An option on Windows is py2exe. This is a third-party module that converts Python programs to executables. As of now, it is only available for Python 2. It can be a little tricky to use. Here is a script that you can use once you have py2exe installed.
import os
program_name = raw_input('Enter name of program: ')
if program_name[-3:]!= '.py':
program_name+='.py'
with open('temp_py2exe.py', 'w') as fp:
s = 'from distutils.core import setup\n'
s += "import py2exe\nsetup(console=['"
s += program_name + "'])"
fp.write(s)
os.system('c:\Python26\python temp_py2exe.py py2exe')
If everything works, a window should pop up and you'll see a bunch of stuff happening quickly. The resulting executable file will show up in a new subdirectory of the directory your Python file is in, called dist. There will be a few other files in that subdirectory that you will need to include with your executable.
Useful modules
Python comes with hundreds of modules that do all sorts of things. There are also many third-party modules available for download from the internet. This chapter discusses a few modules that I have found useful.
Importing modules
There are a couple of different ways to import modules. Here are several ways to import some functions from the Random module.
from random import randint, choice from random import * import random
- The first way imports just two functions from the module.
- The second way imports every function from the module. You should usually avoid doing this, as the module may contain some names that will interfere with your own variable names. For instance if your program uses a variable called
totaland you import a module that contains a function calledtotal, there can be problems. Some modules, however, liketkinter, are fairly safe to import this way. - The third way imports an entire module in a way that will not interfere with your variable names. To use a function from the module, preface it with
randomfollowed by a dot. For instance:random.randint(1,10).
Changing module names
The as keyword can be used to change the name that your program uses to refer to a module or things from a module. Here are three examples:
import numpy as np from itertools import combinations_with_replacement as cwr from math import log as ln
Location
Usually, import statements go at the beginning of the program, but there is no restriction. They can go anywhere as long as they come before the code that uses the module.
Getting help
To get help on a module (say the random module) at the Python shell, import it using the third way above. Then dir(random) gives a list of the functions and variables in the module, and help(random) will give you a rather long description of what everything does. To get help on a specific function, like randint, type help(random.randint).
Dates and times
The time module has some useful functions for dealing with time.
sleep
The sleep function pauses your program for a specified amount of time (in seconds). For instance, to pause your program for 2 seconds or for 50 milliseconds, use the following:
sleep(2) sleep(.05)
Timing things
The time function can be used to time things. Here is an example:
from time import time
start = time()
# do some stuff
print('It took', round(time()-start, 3), 'seconds.')
For another example, see this section, which shows how to put a countdown timer into a GUI.
The resolution of the time() function is milliseconds on Windows and microseconds on Linux. The above example uses whole seconds. If you want millisecond resolution, use the following print statement:
print('{:.3f} seconds'.format(time()-start))
You can use a little math on this to get minutes and hours. Here is an example:
t = time()-start secs = t%60 mins = t//60 hours = mins//60
By the way, when you call time(), you get a rather strange value like 1306372108.045. It is the number of seconds elapsed since January 1, 1970.
Dates
The module datetime allows us to work with dates and times together. The following line creates a datetime object that contains the current date and time:
from datetime import datetime d = datetime(1,1,1).now()
The datetime object has attributes year, month, day, hour, minute, second, and microsecond. Here is a short example:
d = datetime(1,1,1).now()
print('{}:{:02d} {}/{}/{}'.format(d.hour,d.minute,d.month,d.day,d.year))
7:33 2/1/2011
The hour is in 24-hour format. To get 12-hour format, you can do the following:
am_pm = 'am' if d.hour<12 else 'pm'
print('{}:{}{}'.format(d.hour%12, d.minute, am_pm))
An alternative way to display the date and time is to use the strftime method. It uses a variety of formatting codes that allow you to display the date and time, including information about the day of the week, am/pm, etc.
Here are some of the formatting codes:
| Code | Description |
|---|---|
%c | date and time formatted according to local conventions |
%x, %X | %x is the date, and %X is the time, both formatted as with %c |
%d | day of the month |
%j | day of the year |
%a, %A | weekday name (%a is the abbreviated weekday name) |
%m | month (01-12) |
%b, %B | month name (%b is the abbreviated month name) |
%y, %Y | year (%y is 2-digit, %Y is 4-digit) |
%H, %I | hour (%H is 24-hour, %I is 12-hour) |
%p | am or pm |
%M | minute |
%S | second |
Here is an example:
print(d.strftime('%A %x'))
Tuesday 02/01/11
Here is another example:
print(d.strftime('%c'))
print(d.strftime('%I%p on %B %d'))
02/01/11 07:33:14 07AM on February 01
The leading zeros are a little annoying. You could combine strftime with the first way we learned to get nicer output:
print(d.strftime('{}%p on %B {}').format(d.hour%12, d.day))
7AM on February 1
You can also create a datetime object. When doing so, you must specify the year, month, and day. The other attributes are optional. Here is an example:
d = datetime(2011, 2, 1, 7, 33) e = datetime(2011, 2, 1)
You can compare datetime objects using the <, >, ==, and != operators. You can also do arithmetic on datetime objects, though we won't cover it here. In fact, there is a lot more you can do with dates and times.
Another nice module is calendar which you can use to print out calendars and do more sophisticated calculations with dates.
Working with files and directories
The os module and the submodule os.path contain functions for working with files and directories.
Changing the directory
When your program opens a file, the file is assumed to be in the same directory as your program itself. If not, you have to specify the directory, like below:
s = open('c:/users/heinold/desktop/file.txt').read()
If you have a lot of files that you need to read, all in the same directory, you can use os.chdir to change the directory. Here is an example:
os.chdir('c:/users/heinold/desktop/')
s = open('file.txt').read()
Getting the current directory
The function getcwd returns the path of current directory. It will be the directory your program is in or the directory you changed it to with chdir.
Getting the files in a directory
The function listdir returns a list of the entries in a directory, including all files and subdirectories. If you just want the files and not the subdirectories or vice-versa, the os.path module contains the functions isfile and isdir to tell if an entry is a file or a directory. Here is an example that searches through all the files in a directory and prints the names of those files that contain the word 'hello'.
import os
directory = 'c:/users/heinold/desktop/'
files = os.listdir(directory)
for f in files:
if os.path.isfile(directory+f):
s = open(directory+f).read()
if 'hello' in s:
print(f)
Changing and deleting files
Here are a few useful functions. Just be careful here.
| Function | Description |
|---|---|
mkdir | create a directory |
rmdir | remove a directory |
remove | delete a file |
rename | rename a file |
remove function takes a single file name. The first argument
of rename is the old name and the second argument is the new name.
Copying files
There is no function in the os module to copy files. Instead, use the copy function in the shutil module. Here is an example that takes all the files in a directory and makes a copy of each, with each copied file's name starting with Copy of :
import os
import shutil
directory = 'c:/users/heinold/desktop/'
files = os.listdir(directory)
for f in files:
if os.path.isfile(directory+f):
shutil.copy(directory+f, directory+'Copy of '+f)
More with os.path
The os.path module contains several more functions that are helpful for working with files and directories. Different operating systems have different conventions for how they handle paths, and the functions in os.path allow your program to work with different operating systems without having to worry about the specifics of each one. Here are some examples (on my Windows system):
print(os.path.split('c:/users/heinold/desktop/file.txt'))
print(os.path.basename('c:/users/heinold/desktop/file.txt'))
print(os.path.dirname('c:/users/heinold/desktop/file.txt'))
print(os.path.join('directory', 'file.txt'))
('c:/users/heinold/desktop', 'file.txt')
file.txt
c:/users/heinold/desktop
directory\\file.txt
Note that the standard separator in Windows is the backslash. The forward slash also works.
Finally, two other functions you might find helpful are the exists function, which tests if a file or directory exists, and getsize, which gets the size of a file. There are many other functions in os.path. See the Python documentation for more information.
os.walk
The os.walk function allows you to scan through a directory and all of its subdirectories. Here is a simple example that finds all the Python files on my desktop or in subdirectories of my desktop:
for (path, dirs, files) in os.walk('c:/users/heinold/desktop/'):
for filename in files:
if filename[-3:]=='.py':
print(filename)
Running and quitting programs
Running programs
There are a few different ways for your program to run another program. One of them uses the system function in the os module. Here is an example:
import os
os.chdir('c:/users/heinold/desktop')
os.system('file.exe')
The system function can be used to run commands that you can run at a command prompt. Another way to run your programs is to use the execv function.
Quitting your program
The sys module has a function called exit that can be used to quit your program. Here is a simple example:
import sys
ans = input('Quit the program?')
if ans.lower() == 'yes'
sys.exit()
Zip files
A zip file is a compressed file or directory of files. The following code extracts all the files from a zip file, filename.zip, to my desktop:
import zipfile
z = zipfile.ZipFile('filename.zip')
z.extractall('c:/users/heinold/desktop/)
Getting files from the internet
For getting files from the internet there is the urllib module. Here is a simple example:
from urllib.request import urlopen
page = urlopen('http://www.google.com')
s = page.read().decode()
The urlopen function returns an object that is a lot like a file object. In the example above, we use the read() and decode() methods to read the entire contents of the page into a string s.
The string s in the example above is filled with the text of an HTML file, which is not pretty to read. There are modules in Python for parsing HTML, but we will not cover them here. The code above is useful for downloading ordinary text files of data from the internet.
For anything more sophisticated than this, consider using the third party Requests library.
Sound
An easy way to get some simple sounds in your program is to use the winsound module. It only works with Windows, however. One function in winsound is Beep which can be used to play a tone at a given frequency for a given amount of time. Here is an example that plays a sound of 500 Hz for 1 second.
from winsound import Beep Beep(500,1000)
The first argument to Beep is the frequency in Hertz and the second is the duration in milliseconds.
Another function in winsound is PlaySound, which can be used to play WAV files. Here is an example:
from winsound import PlaySound
Playsound('soundfile.wav', 'SND_ALIAS')
On the other hand, If you have Pygame installed, it is pretty easy to play any type of common sound file. This is shown below, and it works on systems other than Windows:
import pygame
pygame.mixer.init(18000,-16,2,1024)
sound = pygame.mixer.Sound('soundfile.wav')
sound.play()
Your own modules
Creating your own modules is easy. Just write your Python code and save it in a file. You can then import your module using the import statement.
Regular expressions
The replace method of strings is used to replace all occurrences of one string with another, and the index method is used to find the first occurrence of a substring in a string. But sometimes you need to do a more a sophisticated search or replace. For example, you may need to find all of the occurrences of a string instead of just the first one. Or maybe you want to find all occurrences of two letters followed by a number. Or perhaps you need to replace every 'qu' that is at the start of a word with 'Qu'. This is what regular expressions are for. Utilities for working with regular expressions are found in the re module.
There is some syntax to learn in order to understand regular expressions. Here is one example to give you an idea of how they work:
import re print(re.sub(r'([LRUD])(\d+)', '***', 'Locations L3 and D22 full.'))
Locations *** and *** full.)
This example replaces any occurrence of an L, R, U, or D followed by one or more digits with '***'.
Introduction
sub
The sub function works as follows:
sub(pattern, replacement, string)
This searches through string for pattern and replaces anything matching that pattern with the string replacement. All of the upcoming examples will be shown with sub, but there are other things we can do with regular expressions besides substituting. We will get to those after discussing the syntax of regular expressions.
Raw strings
A lot of the patterns use backslashes. However, backslashes in strings are used for escape characters, like the newline, \n. To get a backslash in a string, we need to do \\. This can quickly clutter up a regular expression. To avoid this, our patterns will be raw strings, where backslashes can appear as is and don't do anything special. To mark a string as a raw string, preface it with an r like below:
s = r'This is a raw string. Backslashes do not do anything special.'
Syntax
Basic example
We start with a regular expression that mimics the replace method of strings. Here is a example of using replace to replace all occurrences of abc with *:
'abcdef abcxyz'.replace('abc', '*')
*def *xyz
Here is the regular expression code that does the same thing:
re.sub(r'abc', '*', 'abcdef abcxyz')
Square brackets
We can use square brackets to indicate that we only want to match certain letters. Here is an example where we replace every a and d with asterisks:
re.sub(r'[ad]', '*', 'abcdef')
*bc*ef
Here is another example, where an asterisk replaces all occurrences of an a, b, or c that is followed by a 1, 2, or 3:
re.sub(r'[abc][123]', '*', 'a1 + b2 + c5 + x2')
* + * + c5 + x2
We can give ranges of values—for example, [a-j] for the letters a through j. Here are some further examples of ranges:
| Range | Description |
|---|---|
[A-Z] | any capital letter |
[0-9] | any digit |
[A-Za-z0-9] | any letter or digit |
A slightly shorter way to match any digit is \d, instead of [0-9].
Matching any character
Use a dot to match (almost) any character. Here is an example:
re.sub(r'A.B', '*', 'A2B AxB AxxB A$B')
* * AxxB *
The pattern matches an A followed by almost any single character followed by a B.
Exception: The one character not matched by the dot is the newline character. If you need that to be matched, too, put ?s anywhere into your pattern.
Matching multiple copies of something
Here is an example where we match an A followed by one or more B's:
re.sub(r'AB+', '*', 'ABC ABBBBBBC AC)
*C *C AC
We use the + character to indicate that we want to match one or more B's here. There are similar things we can use to specify different numbers of B's here. For instance, using * in place of + will match zero or more B's. (This means that AC in the example above would be replaced by *C because A counts as an A followed by zero B's.) Here is a table of what you can do:
| Code | Description |
|---|---|
+ | match 1 or more occurrences |
* | match 0 or more occurrences |
? | match 0 or 1 occurrence |
{m} | match exactly m occurrences |
{m,n} | match between m and n occurrences, inclusive |
Here is an example that matches an A followed by three to six B's:
re.sub(r'AB{3,6}', '*', 'ABB ABBB ABBBB ABBBBBBBBB')
'ABB * * *BBB'
Here, we do not match ABB because the A is only followed by two B's. The next two pieces get matched, as the A is followed by three B's in the second term, and four B's in the third. In the last piece, there is an A followed by nine B's. What gets matched isthe A along with the first six B's.
Note that the matching in the last piece above is greedy; that is, it takes as many B's as it is allowed. It is allowed to take between three and six B's, and it takes all six. To get the opposite behavior, to get it take as few B's as allowed, add a ?, like below:
re.sub(r'AB{3,6}?', '*', 'ABB ABBB ABBBB ABBBBBBBBB')
'ABB * * *BBBBBB'
The ? can go after any of the numeric specifiers, like +?, -?, ??, etc.
The | character
The | character acts as an “or.” Here is an example:
re.sub(r'abc|xyz', '*', 'abcdefxyz123abc')
'*def*123*'
In the above example, every time we encounter an abc or an xyz, we replace it with an asterisk.
Matching only at the start or end
Sometimes you don't want to match every occurrence of something, maybe just the first or the last occurrence. To match just the first occurrence of something, start the pattern off with the ^ character. To match just the last occurrence, end the pattern with the $ character. Here are some examples:
re.sub('^abc', '*', 'abcdefgabc')
re.sub('abc$', '*', 'abcdefgabc')
*defgabc abcdefg*
Escaping special characters
We have seen that + and * have special meanings. What if we need to match a plus sign? To do so, use the backslash to escape it, like \+. Here is an example:
re.sub(r'AB\+', '*', 'AB+C')
*C
Also, in a pattern, \n represents a newline.
Just a note again about raw strings—if we didn't use them for the patterns, every backslash would have to be doubled. For instance, r'AB\+' would have to be 'AB\\+.
Backslash sequences
-
\dmatches any digit, and\Dmatches any non-digit. Here is an example:re.sub(r'\d', '*', '3 + 14 = 17') re.sub(r'\D', '*', '3 + 14 = 17')
* + ** = ** 3***14***17
-
\wmatches any letter or number, and\Wmatches anything else. Here is an example:re.sub(r'\w', '*', 'This is a test. Or is it?') re.sub(r'\W', '*', 'This is a test. Or is it?')
'**** ** * ****. ** ** **?' 'This*is*a*test***Or*is*it*'
This is a good way to work with words.
-
\smatches whitespace, and\Smatches non-whitespace. Here is an example:re.sub(r'\s', '*', 'This is a test. Or is it?') re.sub(r'\S', '*', 'This is a test. Or is it?')
'This*is*a*test.**Or*is*it?' '**** ** * ***** ** ** ***'
Preceding and following matches
Sometimes you want to match things if they are preceded or followed by something.
| Code | Description |
|---|---|
(?=) | matches only if followed by |
(?!) | matches only if not followed by |
(?<=) | matches only if preceded by |
(?<!) | matches only if not preceded by |
Here is an example that matched the word the only if it is followed by cat:
re.sub(r'the(?= cat)', '*', 'the dog and the cat')
'the dog and * cat'
Here is an example that matches the word the only if it is preceded by a space:
re.sub(r'(?<= )the', '*', 'Athens is the capital.')
Athens is * capital.
The following example will match the word the only if it neither preceded by and nor followed by letters, so you can use it to replace occurrences of the word the, but not occurrences of the within other words.
re.sub(r'(?<!\w)[Tt]he(?!\w)', '*', 'The cat is on the lathe there.')
* cat is on * lathe there.
Flags
There are a few flags that you can use to affect the behavior of a regular expression. We look at a few of them here.
-
(?i)— This is to ignore case. Here is an example:re.sub('(?i)ab', '*', 'ab AB')* *
-
(?s)— Recall the.character matches any character except a newline. This flag makes it match newline characters, too. -
(?x)— Regular expressions can be long and complicated. This flag allows you to use a more verbose, multi-line format, where whitespace is ignored. You can also put comments in. Here is an example:pattern = r"""(?x)[AB]\d+ # Match A or B followed by some digits [CD]\d+ # Match C or D followed by some digits """ print(re.sub(pattern, '*', 'A3C9 and C1B17'))* and *
Summary
There is a lot to remember. Here is a summary:
| Expression | Description |
|---|---|
[] | any of the characters inside the brackets |
. | any character except the newline |
+ | 1 or more of the preceding |
* | 0 or more of the preceding |
? | 0 or 1 of the preceding |
{m} | exactly m of the preceding |
{m,n} | between m and n (inclusive) of the preceding |
? | following +, *, ?, {m}, and {m,n} — take as few as possible |
\ | escape special characters |
| | “or” |
^ | (at start of pattern) match just the first occurrence |
$ | (at end of pattern) match just the last occurrence |
\d\, \D | any digit (non-digit) |
\w\, \W | any letter or number (non-letter or -number) |
\s\, \S | any whitespace (non-whitespace) |
(?=) | only if followed by |
(?!) | only if not followed by |
(?<=) | only if preceded by |
(?<!) | only if not preceded by |
(?i) | flag to ignore case |
(?s) | flag to make the . match newlines, too |
(?x) | flag to enable verbose style |
Here are some short examples:
| Expression | Description |
|---|---|
'abc' | the exact string abc |
'[ABC]' | an A, B, or C |
'[a-zA-Z][0-9]' | match a letter followed by a digit |
'[a..]' | a followed by any two characters (except newlines) |
'a+' | one or more a's |
'a*' | any number of a's, even none |
'a?' | zero or one a |
'a{2}' | exactly two a's |
'a{2,4}' | two, three, or four a's |
'a+?' | one or more a's taking as few as possible |
'a\.' | a followed by a period |
'ab|zy' | an ab or a zy |
'a' | first a |
'a$' | last a |
'\d' | every digit |
'\w' | every letter or number |
'\s' | every whitespace |
'\D' | everything except digits |
'\W' | everything except letters and numbers |
'\S' | everything except whitespace |
'a(?=b)' | every a followed by a b |
'a(?!b)' | every a not followed by a b |
'(?<=b)a' | every a preceded by a b |
'(?<!b)a' | every a not preceded by a b |
Note
Note that in all of the examples in this chapter, we are dealing with non-overlapping patterns. For instance, if we look for the pattern 'aba' in the string 'abababa', we see there are several overlapping matches. All of our matching is done from the left and does not consider overlaps. For instance, we have the following:
re.sub('aba', '*', 'abababa')
'*b*'
Groups
Using parentheses around part of an expression creates a group that contains the text that matches a pattern. You can use this to do more sophisticated substitutions. Here is an example that converts to lowercase every capital letter that is followed by a lowercase letter:
def modify(match):
letters = match.group()
return letters.lower()
re.sub(r'([A-Z])[a-z]', modify, 'PEACH Apple ApriCot')
PEACH apple apricot
The modify function ends up getting called three times, one for each time a match occurs. The re.sub function automatically sends to the modify function a Match object, which we name match. This object contains information about the matching text. The object's group method returns the matching text itself.
If instead of match.group, we use match.groups, then we can further break down the match according the groups defined by the parentheses. Here is an example that matches a capital letter followed by a digit and converts each letter to lowercase and adds 10 to each number:
def modify(match):
letter, number = match.groups()
return letter.lower() + str(int(number)+10)
re.sub(r'([A-Z])(\d)', modify, 'A1 + B2 + C7')
a11 + b12 + c17
The groups method returns the matching text as tuples. For instance, in the above program the tuples returned are shown below:
First match: ('A', '1')
Second match: ('B', '2')
Third match: ('C', '7')
Note also that we can get at this information by passing arguments to match.group. For the first match, match.group(1) is 'A' and match.group(2) is 1.
Other functions
-
sub— We have seen many examples ofsub. One thing we haven't mentioned is that there is an optional argumentcount, which specifies how many matches (from the left) to make. Here is an example:re.sub(r'a', '*', 'ababababa', count=2)
'*b*bababa'
-
findall— Thefindallfunction returns a list of all the matches found. Here is an example:re.findall(r'[AB]\d', 'A3 + B2 + A9')
['A3', 'B2', 'A9']
As another example, to find all the words in a string, you can do the following:
re.findall(r'\w+', s)
This is better than using
s.split()becausesplitdoes not handle punctuation, while the regular expression does. -
split— Thesplitfunction is analogous to the string methodsplit. The regular expression version allows us to split on something more general than the string method does. Here is an example that splits an algebraic expression at+or-.re.split(r'\+|\-', '3x+4y-12x^2+7')
['3x', '4y', '12x2', '7']
-
matchandsearch— These are useful if you just want to know if a match occurs. The difference between these two functions ismatchonly checks to see if the beginning of the string matches the pattern, whilesearchsearches through the string until it finds a match. Both returnNoneif they fail to find a match and a Match object if they do find a match. Here are examples:if (re.match(r'ZZZ', 'abc ZZZ xyz')): print('Match found at beginning.') else: print('No match at beginning') if (re.search(r'ZZZ', 'abc ZZZ xyz')): print('Match found in string.') else: print('No match found.')No match at beginning. Match found in string.
The Match object returned by these functions has group information in it. Say we have the following:
a=re.search(r'([ABC])(\d)', '= A3+B2+C8') a.group() a.group(1) a.group(2)
'A3' 'A' '3'
Remember that
re.searchwill only report on the first match it finds in the string. -
finditer— This returns an iterator of Match objects that we can loop through, like below:for s in re.finditer(r'([AB])(\d)', 'A3+B4'): print(s.group(1))A B
Note that this is a little more general than the
findallfunction in thatfindallreturns the matching strings, whereasfinditerreturns something like a list of Match objects, which give us access to group information. -
compile— If you are going to be reusing the same pattern, you can save a little time by first compiling the pattern, as shown below:pattern = re.compile(r'[AB]\d') pattern.sub('*', 'A3 + B4') pattern.sub('x', 'A8 + B9')* + * x + x
When you compile an expression, for many of the methods you can specify optional starting and ending indices in the string. Here is an example:
pattern = re.compile(r'[AB]\d') pattern.findall('A3+B4+C9+D8',2,6)['B4']
Examples
Roman Numerals
Here we use regular expressions to convert Roman numerals into ordinary numbers.
import re
d = {'M':1000, 'CM':900, 'D':500, 'CD':400, 'C':100, 'XC':90,
'L':50, 'XL':40, 'X':10, 'IX':9, 'V':5, 'IV':4,'I':1}
pattern = re.compile(r"""(?x)
(M{0,3})(CM)?
(CD)?(D)?(C{0,3})
(XC)?(XL)?(L)?(X{0,3})
(IX)?(IV)?(V)?(I{0,3})""")
num = input('Enter Roman numeral: ').upper()
m = pattern.match(num)
sum = 0
for x in m.groups():
if x!=None and x!='';:
if x in ['CM', 'CD', 'XC', 'XL', 'IX', 'IV']:
sum+=d[x]
elif x[0] in 'MDCLXVI':
sum+=d[x[0]]*len(x)
print(sum)
Enter Roman numeral: MCMXVII 1917
The regular expression itself is fairly straightforward. It looks for up to three M's, followed by zero or one CM's, followed by zero or one CD's, etc., and stores each of those in a group. The for loop then reads through those groups and uses a dictionary to add the appropriate values to a running sum.
Dates
Here we use a regular expression to take a date in a verbose format, like February 6, 2011, and convert it an abbreviated format, mm/dd/yy (with no leading zeroes). Rather than depend on the user to enter the date in exactly the right way, we can use a regular expression to allow for variation and mistakes. For instance, this program will work whether the user spells out the whole month name or abbreviates it (with or with a period). Capitalization does not matter, and it also does not matter if they can even spell the month name correctly. They just have to get the first three letters correct. It also does not matter how much space they use and whether or not they use a comma after the day.
import re
d = {'jan':'1', 'feb':'2', 'mar':'3', 'apr':'4',
'may':'5', 'jun':'6', 'jul':'7', 'aug':'8',
'sep':'9', 'oct':'10', 'nov':'11', 'dec':'12'}
date = input('Enter date: ')
m = re.match('([A-Za-z]+)\.?\s*(\d{1,2}),?\s*(\d{4})', date)
print('{}/{}/{}'.format(d[m.group(1).lower()[:3]],
m.group(2), m.group(3)[-2:]))
Enter date: feb. 6, 2011 2/6/11
The first part of the regular expression, ([A-Za-z]+)\.? takes care of the month name. It matches however many letters the user gives for the month name. The \.? matches either 0 or 1 periods after the month name, so the user can either enter a period or not. The parentheses around the letters save the result in group 1.
Next we find the day: \s*(\d{1,2}). The first part \s* matches zero or more whitespace characters, so it doesn't matter how much space the user puts between the month and day. The rest matches one or two digits and saves it in group 2.
The rest of the expression, ,?\s*(\d{4}), finds the year. Then we use the results to create the abbreviated date. The only tricky part here is the first part, which takes the month name, changes it to all lowercase, and takes only the first three characters and uses those as keys to a dictionary. This way, as long as the user correctly spells the first three letters of the month name, the program will understand it.
Math
This chapter is a collection of topics that are at somewhat mathematical in nature, though many of them are of general interest.
The math module
As mentioned in this section, the math module contains some common math functions. Here are most of them:
| Function | Description |
|---|---|
sin, cos, tan | trig functions |
asin, acos, atan | inverse trig functions |
atan2(y,x) | gives arctan(y/x) with proper sign behavior |
sinh, cosh, tanh | hyperbolic functions |
asinh, acosh, atanh | inverse hyperbolic functions |
log, log10 | natural log, log base 10 |
log1p | log(1+x), more accurate near 1 than log |
exp | exponential function ex |
degrees, radians | convert from radians to degrees or vice-versa |
floor | floor(x) is the greatest integer ≤ x |
ceil | ceil(x) is the least integer ≥ x |
e, pi | the constants e and π |
factorial | factorial |
modf | returns a pair (fractional part, integer part) |
gamma, erf | the Γ function and the Error function |
Note
Note that thefloor and int functions behave the same for positive numbers, but differently for negative numbers. For instance, floor(3.57) and int(3.57) both return the integer 3. However, floor(-3.57) returns -4, the greatest integer less than or equal to -3.57, while int(-3.57) returns -3, which is obtained by throwing away the decimal part of the number.
atan2
The atan2 function is useful for telling the angle between two points. Let x and y be the distances between the points in the x and y directions. The tangent of the angle in the picture below is given by y/x. Then arctan(y/x) gives the angle itself.
But if the angle were 90°, this would not work as x would be 0. We would also need special cases to handle when x<0 and when y<0. The atan2 function handles all of this. Doing atan2(y,x) will return arctan(y/x) with all of the cases handled properly.
The atan2 function returns the result in radians. If you would like degrees, do the following:
angle = math.degrees(atan2(y,x))
The resulting angle from atan2 is between -π and π (-180° and 180°). If you would like it between 0 and 360°, do the following:
angle = math.degrees(atan2(y,x)) angle = (angle+360) % 360
Scientific notation
Look at the following code:
100.1**10
1.0100451202102516e+20
The resulting value is displayed in scientific notation. It is 1.0100451202102516 × 1020. The e+20 stands for × 1020. Here is another example:
.15**10
5.7665039062499975e-09
This is 5.7665039062499975 × 10-9.
Comparing floating point numbers
In this section we saw that some numbers, like .1, are not represented exactly on a computer. Mathematically, after the code below executes, x should be 1, but because of accumulated errors, it is actually 0.9999999999999999.
x = 0
for i in range(10):
x+=.1
This means that the following if statement will turn out False:
if x==1:
A more reliable way to compare floating point numbers x and y is to check to see if the difference between the two numbers is sufficiently small, like below:
if abs(x-y)<10e-12:
Fractions
There is a module called fractions for working with fractions. Here is a simple example of it in action:
from fractions import Fraction r = Fraction(3, 4) s = Fraction(1, 4) print(r+s)
Fraction(1, 1)
You can do basic arithmetic with Fraction objects, as well as compare them, take their absolute values, etc. Here are some further examples:
r = Fraction(3, 4)
s = Fraction(2, 8)
print(s)
print(abs(2*r-3))
if r>s:
print('r is larger')
Fraction(1,4) Fraction(3,2) r is larger
Note that Fraction automatically converts things to lowest terms. The example below shows how to get the numerator and denominator:
r = Fraction(3,4) r.numerator r.denominator
3 4
Converting to and from floats
To convert a fraction to a floating point number, use float, like below:
float(Fraction(1, 8))
0.125
On the other hand, say we want to convert 0.3 to a fraction. Unfortunately, we should not do Fraction(.3) because, as mentioned, some numbers, including .3, are not represented exactly on the computer. In fact, Fraction(.3) returns the following Fraction object:
Fraction(5404319552844595, 18014398509481984)
Instead, use string notation, like below:
Fraction('.3')
Limiting the denominator
One useful method is limit_denominator. For a given Fraction object, limit_denominator(x) finds the closest fraction to that value whose denominator does not exceed x. Here is some examples:
Fraction('.333').limit_denominator(100)
Fraction('.333').limit_denominator(1000)
Fraction('3.14159').limit_denominator(1000)
Fraction(1, 3) Fraction(333, 1000) Fraction(355, 113)
The last example returns a pretty close fractional approximation to π. It is off by less than 0.0000003.
Greatest common divisor
The fractions module contains a useful function called gcd that returns the greatest common divisor of two numbers. Here is an example:
from fractions import gcd
print('The largest factor 35 and 21 have in common is', gcd(35, 21))
The largest factor 35 and 21 have in common is 7
The decimal module
Python has a module called decimal for doing exact calculations with decimal numbers. As we've noted a few times now, some numbers, such as .3, cannot be represented exactly as a float. Here is how to get an exact decimal representation of .3:
from decimal import Decimal
Decimal('.3')
Decimal('0.3')
The string here is important. If we leave it out, we get a decimal that corresponds with the inexact floating point representation of .3:
Decimal(.3)
Decimal('0.29999999999999998889776975374843459576368
3319091796875')
Math
You can use the usual math operators to work with Decimal objects. For example:Decimal(.34) + Decimal(.17)
Decimal('0.51')
Here is another example:
Decimal(1) / Decimal(17)
Decimal('0.05882352941176470588235294118')
The mathematical functions exp, ln, log10, and sqrt are methods of decimal objects. For instance, the following gives the square root of 2:
Decimal(2).sqrt()
Decimal('1.414213562373095048801688724')
Decimal objects can also be used with the built in max, min, and sum functions, as well as converted to floats with float and strings with str.
Precision
By default Decimal objects have 28-digit precision. To change it to, say, five digit-precision, use the getcontext function.
from decimal import getcontext getcontext().prec = 5
Here is an example that prints out 100 digits of √2:
getcontext().prec = 100 Decimal(2).sqrt()
Decimal('1.414213562373095048801688724209698078569671875
376948073176679737990732478462107038850387534327641573')
There is theoretically no limit to the precision you can use, but the higher the precision, the more memory is required and the slower things will run. In general, even with small precisions, Decimal objects are slower than floating point numbers. Ordinary floating point arithmetic is enough for most problems, but it is nice to know that you can get higher precision if you ever need it.
There is a lot more to the decimal module. See the Python documentation.
Complex numbers
Python has a data type for complex numbers.
In math, we have i=√-1. The number i is called an imaginary number. A complex number is a number of the form a+bi, where a and b are real numbers. The value a is called the real part, and b is the imaginary part. In electrical engineering, the symbol j is used in place of i, and in Python j is used for imaginary numbers. Here are a couple of examples of creating complex numbers:
x = 7j x = 1j x = 3.4 + .3j x = complex(3.4, .3)
If a number ends in a j or J, Python treats it as a complex number.
Complex numbers have methods real() and imag() which return the real and imaginary parts of the number. The conjugate method returns the complex conjugate (the conjugate of a+bi is a-bi).
The cmath module contains many of the same functions as the math module, except that they work with complex arguments. The functions include regular, inverse, and hyperbolic trigonometric functions, logarithms and the exponential function. It also contains two functions, polar and rect, for converting between rectangular and polar coordinates:
cmath.polar(3j) cmath.rect(3.0, 1.5707963267948966)
(3.0, 1.5707963267948966) (1.8369701987210297e-16+3j)
Complex numbers are fascinating, though not all that useful in day-to-day life. One nice application, however, is fractals. Here is a program that draws the famous Mandelbrot set. The program requires the PIL and Python 2.6 or 2.7.
from Tkinter import *
from PIL import Image, ImageTk, ImageDraw
def color_convert(r, g, b):
return '#{0:02x}{1:02x}{2:02x}'.format(int(r*2.55),int(g*2.55),
int(b*2.55))
max_iter=75
xtrans=-.5
ytrans=0
xzoom=150
yzoom=-150
root = Tk()
canvas = Canvas(width=300, height=300)
canvas.grid()
image=Image.new(mode='RGB',size=(300,300))
draw = ImageDraw.Draw(image)
for x in range(300):
c_x = (x-150)/float(xzoom)+xtrans
for y in range(300):
c = complex(c_x, (y-150)/float(yzoom)+ytrans)
count=0
z=0j
while abs(z)≤2 and count<max_iter:
z = z*z+c
count += 1
draw.point((x,y),
fill=color_convert(count+25,count+25,count+25))
canvas.delete(ALL)
photo=ImageTk.PhotoImage(image)
canvas.create_image(0,0,image=photo,anchor=NW)
canvas.update()
mainloop()

The code here runs very slowly. There are ways to speed it up somewhat, but Python is unfortunately slow for these kinds of things.
More with lists and arrays
Sparse lists
A 10,000,000 × 10,000,000 list of integers requires several hundred terabytes of storage, far more than most hard drives can store. However, in many practical applications, most of the entries of a list are 0. This allows us to save a lot of memory by just storing the nonzero values along with their locations. We can do this using a dictionary whose keys are the locations of the nonzero elements and whose values are the values stored in the array at those locations. For example, suppose we have a two-dimensional list L whose entries are all zero except that L[10][12] is 47 and L[100][245] is 18. Here is a the dictionary that we would use:
d = {(10,12): 47, (100,245): 18}
The array module
Python has a module called array that defines an array object that behaves a lot like a list, except that its elements must all be the same type. The benefit of array over lists is more efficient memory usage and faster performance. See the Python documentation for more about arrays.
The NumPy and SciPy libraries
If you have any serious mathematical or scientific calculations to do on arrays, you may want to consider the NumPy library. It is easy to download and install. From the NumPy user's guide:
NumPy is the fundamental package for scientific computing in Python. It is a Python library that provides a multidimensional array object, various derived objects (such as masked arrays and matrices), and an assortment of routines for fast operations on arrays, including mathematical, logical, shape manipulation, sorting, selecting, I/O, discrete Fourier transforms, basic linear algebra, basic statistical operations, random simulation and much more.
There is also SciPy, which builds off of NumPy. This time from the SciPy user's guide:
SciPy is a collection of mathematical algorithms and convenience functions built on the NumPy extension for Python. It adds significant power to the interactive Python session by exposing the user to high-level commands and classes for the manipulation and visualization of data. With SciPy, an interactive Python session becomes a data-processing and system-prototyping environment rivaling sytems such as MATLAB, IDL, Octave, R-Lab, and SciLab.
Random numbers
How Python generates random numbers
The random number generator that Python uses is called the Mersenne Twister. It is reliable and well-tested. It is a deterministic generator, meaning that it uses a mathematical process to generate random numbers. The numbers are called pseudorandom numbers because, coming from a mathematical process, they are not truly random, though, for all intents and purposes, they appear random. Anyone who knows the process can recreate the numbers. This is good for scientific and mathematical applications, where you want to be able to recreate the same random numbers for testing purposes, but it is not suitable for cryptography, where you need to generate truly random numbers.
Seeds
For mathematical and scientific applications, you may want to reproduce the same random numbers each time you run your program, in order to test your work with the same data. You can do this by specifying the seed. Examples are shown below:
random.seed(1)
print("Seed 1:", [random.randint(1,10) for i in range(5)])
random.seed(2)
print("Seed 2:", [random.randint(1,10) for i in range(5)])
random.seed(1)
print("Seed 1:",[random.randint(1,10) for i in range(5)])
Seed 1: [2, 9, 8, 3, 5] Seed 2: [10, 10, 1, 1, 9] Seed 1: [2, 9, 8, 3, 5]
The seed can be any integer. If we just use random.seed(), then the seed will be more or less randomly selected based off of the system clock.
The random function
Most of the functions in the random module are based off of the random function, which uses the Mersenne Twister to generate random numbers between 0 and 1. Mathematical transformations are then used on the result of random to get some of the more interesting random number functions.
Other functions in the random module
The random module contains functions that return random numbers from various distributions, like the Gaussian or exponential distributions. For instance, to generate a Gaussian (normal) random variable, use the gauss function. Here are some examples:
random.gauss(64,3.5) [round(random.gauss(64,3.5),1) for i in range(10)]
61.37965975173485 [58.4, 61.0, 67.0, 67.9, 63.2, 65.0, 64.5, 63.4, 65.5, 67.3]
The first argument of gauss is the mean and the second is the standard deviation. If you're not familiar with normal random variables, they are the standard bell curve. Things like heights and SAT scores and many other real-life things approximately fit this distribution. In the example above, the random numbers generated are centered around 64. Numbers closer to 64 are more likely to be generated than numbers farther away.
There are a bunch of other distributions that you can use. The most common is the uniform distribution, in which all values in a range are equally likely. For instance:
random.uniform(3,8)
7.535110252245726
See the Python documentation for information on the other distributions.
A more random randint function
One way to generate cryptographically safe random numbers is to use some fairly random physical process. Examples include radioactive decay, atmospheric phenomena, and the behavior of certain electric circuits. The os module has a function urandom that generates random numbers from a physical process whose exact nature depends on your system. The urandom function takes one argument telling it how many bytes of random data to produce. Calling urandom(1) produces one byte of data, which we can translate to an integer between 0 and 255. Calling urandom(2) produces two bytes of data, translating to integers between 0 and 65535. Here is a function that behaves like randint, but uses urandom to give us nondeterministic random numbers:
from os import urandom
from math import log
def urandint(a,b):
x = urandom(int(log(b-a+1)/log(256))+1)
total = 0
for (i,y) in enumerate(x):
total += y*(2**i)
return total%(b-a+1)+a
The way this works is we first have to determine how many bytes of random data to generate. Since one byte gives 256 possible values and two bytes give 2562 possible values, etc., we compute the log base 256 of the size of the range b-a+1 to determine how many byes to generate. We then loop through the bytes generated and convert them to an integer. Finally, modding that integer by b-a+1 reduces that integer to a number between 0 and b-a+1, and adding a to that produces an integer in the desired range.
Miscellaneous topics
Hexadecimal, octal, and binary
Python has built-in functions hex, oct, and bin for converting integers to hexadecimal, octal, and binary. The int function converts those bases to base 10. Here are some examples:
hex(250) oct(250) bin(250) int(0xfa)
'0xfa' '0o372' '0b11111010' 250
Hexadecimal values are prefaced with 0x, octal values are prefaced with 0o and binary values are prefaced with 0b.
The int function
The int function has an optional second argument that allows you to specify the base you are converting from. Here are a few examples:
int('101101', 2) # convert from base 2
int('121212', 3) # convert from base 3
int('12A04', 11) # convert from base 11
int('12K04', 23) # convert from base 23
45 455 18517 314759
The pow function
Python has a built-in function called pow, which raises numbers to powers. It behaves like the ** operator, except that it takes an optional third argument that specifies a modulus. Thus pow(x,y,n) returns (x**y)%n. The reason you might want to use this is that the pow way is much quicker when very large numbers are involved, which happens a lot in cryptographic applications.
Using the Python shell as a calculator
I often use the Python shell as a calculator. This section contains a few tips for working at the shell.
Importing math functions
One good way to start a session at the shell is to import some math functions:
from math import *
Special variable
There is a special variable _ which holds the value of the previous calculation. Here is an example:
>>> 23**2 529 >>> _+1 530
Logarithms
I use the natural logarithm a lot, and it is more natural for me to type ln instead of log. If you want to do that, just do the following:
ln = log
Summing a series
Here is a way to get an approximate sum of a series, in this case Σ∞n=1 1/(n2-1):
>>> sum([1/(n**2-1) for n in range(2,1000)]) 0.7489994994995
Another example:
Say you need the sine of each of the angles 0, 15, 30, 45, 60, 75, and 90. Here is a quick way to do that:
>>> [round(sin(radians(i)),4) for i in range(0,91,15)] [0.0, 0.2588, 0.5, 0.7071, 0.866, 0.9659, 1.0]
Third-party modules
There are a number of other third-party modules that you might find useful when working in the Python shell. For instance, there is Numpy and Scipy, which we mentioned in this section. There is also Matplotlib, a versatile library for plotting things, and there is Sympy, which does symbolic computations.
Working with functions
This chapter covers a number of topics to do with functions, including some topics in functional programming.
First-class functions
Python functions are said to be first-class functions, which means they can be assigned to variables, copied, used as arguments to other functions, etc., just like any other object.
Copying functions
Here is an example where we make a copy of a function:
def f(x):
return x*x
g = f
print('f(3) =', f(3), 'g(3) =', g(3), sep = '\n')
f(3) = 9 g(3) = 9
Lists of functions
Next, we have a list of functions:
def f(x):
return x**2
def g(x):
return x**3
funcs = [f, g]
print(funcs[0](5), funcs[1](5), sep='\n')
25 125
Here is another example. Say you have a program with ten different functions and the program has to decide at runtime which function to use. One solution is to use ten if statements. A shorter solution is to use a list of functions. The example below assumes that we have already created functions f1, f2, …, f10, that each take two arguments.
funcs = [f1, f2, f3, f4, f5, f6, f7, f8, f9, f10]
num = eval(input('Enter a number: '))
funcs[num]((3,5))
Functions as arguments to functions
Say we have a list of 2-tuples. If we sort the list, the sorting is done based off of the first entry as below:
L = [(5,4), (3,2), (1,7), (8,1)] L.sort()
[(1, 7), (3, 2), (5, 4), (8, 1)]
Suppose we want the sorting to be done based off the second entry. The sort method takes an optional argument called key, which is a function that specifies how the sorting should be done. Here is how to sort based off the second entry:
def comp(x):
return x[1]
L = [(5,4), (3,2), (1,7), (8,1)]
L.sort(key=comp)
[(8, 1), (3, 2), (5, 4), (1, 7)]
Here is another example, where we sort a list of strings by length, rather than alphabetically.
L = ['this', 'is', 'a', 'test', 'of', 'sorting'] L.sort(key=len)
['a', 'is', 'of', 'this', 'test', 'sorting']
One other place we have seen functions as arguments to other functions is the callback functions of Tkinter buttons.
Anonymous functions
In one of the examples above, we passed a comparison function to the sort method. Here is the code again:
def comp(x):
return x[1]
L.sort(key=comp)
If we have a really short function that we're only going to use once, we can use what is called an anonymous function, like below:
L.sort(key=lambda x: x[1])
The lambda keyword indicates that what follows will be an anonymous function. We then have the arguments to the function, followed by a colon and then the function code. The function code cannot be longer than one line.
We used anonymous functions back when working with GUIs to pass information about which button was clicked to the callback function. Here is the code again:
for i in range(3):
for j in range(3):
b[i][j] = Button(command = lambda x=i,y=j: function(x,y))
Recursion
Recursion is the process where a function calls itself. One of the standard examples of recursion is the factorial function. The factorial, n!, is the product of all the numbers from 1 up to n. For instance, 5!=5·4·3·2·1=120. Also, by convention, 0!=1. Recursion involves defining a function in terms of itself. Notice that, for example, 5!=5· 4!, and in general, n!=n· (n-1)!. So the factorial function can be defined in terms of itself. Here is a recursive version of the factorial function:
def fact(n):
if n==0:
return 1
else:
return n*fact(n-1)
We must specify the n=0 case or else the function would keep calling itself forever (or at least until Python generates an error about too many levels of recursion).
Note that the math module has a function called factorial, so this version here is just for demonstration. Note also that there is a non-recursive way to do the factorial, using a for loop. It is about as straightforward as the recursive way, but faster. However, for some problems the recursive solution is the more straightforward solution. Here, for example, is a program that factors a number into prime factors.
def factor(num, L=[]):
for i in range(2,num//2+1):
if num%i==0:
return L+[i]+factor(num//i)
return L+[num]
The factor function takes two arguments: a number to factor, and a list of previously found factors. It checks for a factor, and if it finds one, it appends it to the list. The recursive part is that it divides the number by the factor that was found and then appends to the list all the factors of that value. On the other hand, if the function doesn't find any factors, it appends the number to the list, as it must be a prime, and returns the new list.
map, filter, reduce, and list comprehensions
map and filter
Python has a built-in functions called map and filter that are used to apply functions to the contents of a list. They date back to before list comprehensions were a part of Python, but now list comprehensions can accomplish everything these functions can. Still, you may occasionally see code using these functions, so it is good to know about them.
The map function takes two arguments—a function and an iterable—and it applies the function to each element of the iterable, generating a new iterable. Here is an example that takes a list of strings a returns a list of the lengths of the strings. The first line accomplishes this with map, while the second line uses list comprehensions:
L = list(map(len, ['this', 'is', 'a', 'test'])) L = [len(word) for word in ['this', 'is', 'a', 'test']]
The function filter takes a function and an iterable and returns an iterable of all the elements of the list for which the function is true. Here is an example that returns all the words in a list that have length greater than 2. The first line uses filter to do this, and the second line does it with a list comprehension:
L = list(filter(lambda x: len(x)>2, ['this', 'is', 'a', 'test'])) L = [word for word in ['this', 'is', 'a', 'test'] if len(word)>2]
Here is one approach to finding the number of items in a list L that are greater than 60:
count=0
for i in L:
if i>60:
count = count + 1
Here is a second way using a list comprehension similar to the filter function:
len([i for i in L if i>60])
The second way is both shorter and easier to understand.
reduce
There is another function, reduce, that applies a function to the contents of a list. It used to be a built-in function, but in Python 3 it has also been moved to the functools module. This function cannot be easily replaced with list comprehensions. To understand it, first consider a simple example that adds up the numbers from 1 to 100.
total = 0
for i in range(1,101):
total = total + i
The reduce function can be used to do this in a single line:
total = reduce(lambda x,y: x+y, range(1,101))
In general, reduce takes a function and an iterable, and applies the function to the elements from left to right, accumulating the result. As another simple example, the factorial function could be implemented using reduce:
def fact(n):
return reduce(lambda x,y:x*y, range(1,n+1))
The operator module
In the previous section, when we needed a function to represent a Python operator like addition or multiplication, we used an anonymous function, like below:
total = reduce(lambda x,y: x+y, range(1,101))
Python has a module called operator that contains functions that accomplish the same thing as Python operators. These will run faster than anonymous functions. We can rewrite the above example like this:
from operator import add total = reduce(add, range(1,101))
The operator module has functions corresponding arithmetic operators, logical operators, and even things like slicing and the in operator.
More about function arguments
You may want to write a function for which you don't know how many arguments will be passed to it. An example is the print function where you can enter however many things you want to print, each separated by commas.
Python allows us to declare a special argument that collects several other arguments into a tuple. This syntax is demonstrated below:
def product(*nums):
prod = 1
for i in nums:
prod*=i
return prod
print(product(3,4), product(2,3,4), sep='\n')
12 24
There is a similar notation, **, for collecting an arbitrary number of keyword arguments into a dictionary. Here is a simple example:
def f(**keyargs):
for k in keyargs:
print(k, '**2 : ', keyargs[k]**2, sep='';)
f(x=3, y=4, z=5)
y**2 : 16 x**2 : 9 z**2 : 25
You can also use these notations together with ordinary arguments. The order matters—arguments collected by * have to come after all positional arguments and arguments collected by ** always come last. Two example function declarations are shown below:
def func(a, b, c=5, *d, **e): def func(a, b, *c, d=5, **e):
Calling functions
The * and ** notations can be used when calling a function, too. Here is an example:
def f(a,b):
print(a+b)
x=(3,5)
f(*x)
This will print 8. In this case we could have more simply called f(3,5), but there are situations when that is not possible. For example, maybe you have several different sets of arguments that your program might use for a function. You could have several if statements, but if there are a lot of different sets of arguments, then the * notation is much easier. Here is a simple example:
def f(a,b):
print(a+b)
args = [(1,2), (3,4), (5,6), (7,8), (9,10)]
i = eval(input('Enter a number from 0 to 4: '))
f(*args[i])
One use for the ** notation is simplifying Tkinter declarations. Suppose we have several widgets that all have the same properties, say the same font, foreground color, and background color. Rather than repeating those properties in each declaration, we can save them in a dictionary and then use the ** notation in the declarations, like below:
args = {'fg':'blue', 'bg':'white', 'font':('Verdana', 16, 'bold')}
label1 = Label(text='Label 1', **args)
label2 = Label(text='Label 2', **args)
apply
Python 2 has a function called apply which is, more or less, the equivalent of * and ** for calling functions. You may see it in older code.
Function variables that retain their values between calls
Sometimes it is useful to have variables that are local to a function that retain their values between function calls. Since functions are objects, we can accomplish this by adding a variable to the function as if it were a more typical sort of object. In the example below the variable f.count keeps track of how many times the function is called.
def f():
f.count = f.count+1
print(f.count)
f.count=0
The itertools and collections modules
The itertools and collections modules contain functions that can greatly simplify some common programming tasks. We will start with some functions in itertools.
Permutations and combinations
Permutations
The permutations of a sequence are rearrangements of the items of that sequence. For example, some permutations of [1,2,3] are [3,2,1] and [1,3,2]. Here is an example that shows all the possibilities:
list(permutations([1,2,3]))
[(1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1)]
We can find the permutations of any iterable. Here are the permutations of the string '123':
['';.join(p) for p in permutations('123')]
['123', '132', '213', '231', '312', '321']
The permutations function takes an optional argument that allows us to specify the size of the permutations. For instance, if we just want all the two-element substrings possible from '123', we can do the following:
['';.join(p) for p in permutations('123', 2)]
['12', '13', '21', '23', '31', '32']
Note that permutations and most of the other functions in the itertools module return an iterator. You can loop over the items in an iterator and you can use list to convert it to a list.
Combinations
If we want all the possible k-element subsets from a sequence, where all that matters is the elements, not the order in which they appear, then what we want are combinations. For instance, the 2-element subsets that can be made from {1,2,3} are {1,2}, {1,3} and {2,3}. We consider {1,2} and {2,1} as being the same because they contain the same elements. Here is an example showing the combinations of two-element substrings possible from '123':
['';.join(c) for c in combinations('123', 2)]
['12', '13', '23']
Combinations with replacement
For combinations with repeated elements, use the function combinations_with_replacement.
['';.join(c) for c in combinations_with_replacement('123', 2)]
['11', '12', '13', '22', '23', '33']
Cartesian product
The function product produces an iterator from the Cartesian product of iterables. The Cartesian product of two sets X and Y consists of all pairs (x,y) where x is in X and y is in Y. Here is a short example:
['';.join(p) for p in product('abc', '123')]
['a1', 'a2', 'a3', 'b1', 'b2', 'b3', 'c1', 'c2', 'c3']
Example
To demonstrate the use ofproduct, here are three progressively shorter, and clearer ways to find all one- or two-digit Pythagorean triples (values of (x,y,z) satisfying x2+y2=z2). The first way uses nested for loops:
for x in range(1,101):
for y in range(1,101):
for z in range(1,101):
if x**2+y**2==z**2:
print(x,y,z)
Here is the same thing rewritten with product:
X = range(1,101)
for (x,y,z) in product (X,X,X):
if x**2+y**2==z**2:
print(x,y,z)
It is even shorter if we use list comprehensions:
X = range(1,101) [(x,y,z) for (x,y,z) in product(X,X,X) if x**2+y**2==z**2]
Grouping things
The groupby function is handy for grouping things. It breaks a list up into groups by tracing through the list and every time there is a change in values, a new group is created. The groupby function returns ordered pairs that consist of a list item and groupby iterator object that contains the group of items.
L = [0, 0, 1, 1, 1, 2, 0, 4, 4, 4, 4, 4]
for key,group in groupby(L):
print(key, ':', list(group))
0 : [0, 0] 1 : [1, 1, 1] 2 : [2] 0 : [0] 4 : [4, 4, 4, 4, 4]
Notice that we get two groups of zeros. This is because groupby returns a new group each time there is a change in the list. In the above example, if we instead just wanted to know how many of each number occur, we can first sort the list and then call groupby.
L = [0, 0, 1, 1, 1, 2, 0, 4, 4, 4, 4, 4]
L.sort()
for key,group in groupby(L):
print(key, ':', len(list(group)))
0 : 3 1 : 3 2 : 1 4 : 5
Most of the time, you will want to sort your data before calling groupby.
Optional argument
The groupby function takes an optional argument that is a function telling it how to group things. When using this, you usually have to first sort the list with that function as the sorting key. Here is an example that groups a list of words by length:
L = ['this', 'is', 'a', 'test', 'of', 'groupby']
L.sort(key = len)
for key,group in groupby(L, len):
print(key, ':', list(group))
1 : ['a'] 2 : ['is', 'of'] 4 : ['test', 'this'] 7 : ['groupby']
Examples
We close this section with two examples.
First, suppose L is a list of zeros and ones, and we want to find out how long the longest run of ones is. We can do that in one line using groupby:
max([len(list(group)) for key,group in groupby(L) if key==1])
Second, suppose we have a function called easter that returns the date of Easter in a given year. The following code will produce a histogram of which dates occur most often from 1900 to 2099.
L = [easter(Y) for Y in range(1900,2100)]
L.sort()
for key,group in groupby(L):
print(key, ':', '*'*(len(list(group)))
Miscellaneous things from itertools
chain
The chain function chains iterators together into one big iterator. For example, if you have three lists, L, M, and N and want to print out all the elements of each, one after another, you can do the following:
for i in chain(L,M,N):
print(i)
As another example, in this section we used list comprehensions to flatten a list of lists, that is to return a list of all the elements in the lists. Here is another way to do that using chain:
L = [[1,2,3], [2,5,5], [7,8,3]] list(chain(*tuple(L)))
[1, 2, 3, 2, 5, 5, 7, 8, 3]
count
The function count() behaves like range(∞). It takes an optional argument so that count(x) behaves like range(x,∞).
cycle
The cycle function cycles over the elements of the iterator continuously. When it gets to the end, it starts over at the beginning, and keeps doing this forever. The following simple example prints the numbers 0 through 4 continuously until the user enters an 'n':
for x in cycle(range(5)):
z = input('Keep going? y or n: ')
if z=='n':
break
print(x)
More about iterators
There are a number of other functions in the itertools module. See the Python documentation for more. It has a nice table summarizing what the various functions do.
Counting things
The collections module has a useful class called Counter. You feed it an iterable and the Counter object that is created is something very much like a dictionary whose keys are items from the sequence and whose values are the number of occurrences of the keys. In fact, Counter is a subclass of dict, Python's dictionary class. Here is an example:
Counter('aababcabcdabcde')
Counter({'a': 5, 'b': 4, 'c': 3, 'd': 2, 'e': 1})
Since Counter is a subclass of dict, you can access items just like in a dictionary, and most of the usual dictionary methods work. For example:
c = Counter('aababcabcdabcde')
c['a']
list(c.keys())
list(c.values())
5 ['a', 'c', 'b', 'e', 'd'] [5, 3, 4, 1, 2]
Getting the most common items
This most_common method takes an integer n and returns a list of the n most common items, arranged as (key, value) tuples. For example:
c = Counter('aababcabcdabcde')
c.most_common(2)
[('a', 5), ('b', 4)]
If we omit the argument, it returns tuples for every item, arranged in decreasing order of frequency. To get the least common elements, we can use a slice from the end of the list returned by most_common. Here is some examples:
c = Counter('aababcabcdabcde')
c.most_common()
c.most_common()[-2:]
c.most_common()[-2::-1]
[('a', 5), ('b', 4), ('c', 3), ('d', 2), ('e', 1)]
[('d', 2), ('e', 1)]
[('d', 2), ('c', 3), ('b', 4), ('a', 5)]
The last example uses a negative slice index to reverse the order to least to most common.
An example
Here is a really short program that will scan through a text file and create a Counter object of word frequencies.
from collections import Counter
import re
s = open('filename.txt').read())
words = re.findall('\w+', s.lower())
c = Counter(words)
To print the ten most common words, we can do the following:
for word, freq in c.most_common(10):
print(word, ':', freq)
To pick out only those words that occur more than five times, we can do the following:
[word for word in c if c[word]>5]
Math with counters
You can use some operators on Counter objects. Here is some examples:
c = Counter('aabbb')
d = Counter('abccc')
c+d
c-d
c&d
c|d
Counter({'b': 4, 'a': 3, 'c': 3})
Counter({'b': 2, 'a': 1})
Counter({'a': 1, 'b': 1})
Counter({'c': 3, 'b': 3, 'a': 2})
Doing c+d combines the counts from c and d, whereas c-d subtracts the counts from d from the corresponding counts of c. Note that the Counter returned by c-d does not include 0 or negative counts. The & stands for intersection and returns the minimum of the two values for each item, and | stands for union and returns the maximum of the two values.
defaultdict
The collections module has another dictionary-like class called defaultdict. It is almost exactly like an ordinary dictionary except that when you create a new key, a default value is given to the key. Here is an example that mimics what the Counter class does.
s = 'aababcabcdabcd'
dd = defaultdict(int)
for c in s:
dd[c]+=1
defaultdict(<class 'int'>, {'a': 5, 'c': 3, 'b': 4, 'd': 2})
If we had tried this with dd just a regular dictionary, we would have gotten an error the first time the program reached dd[c]+=1 because dd[c] did not yet exist. But since we declared dd to be defaultdict(int), each value is automatically assigned a value of 0 upon creation, and so we avoid the error. Note that we could use a regular dictionary if we add an if statement into the loop, and there is also a function of regular dictionaries that allows you to set a default value, but defaultdict runs faster.
We can use types other than integers. Here is an example with strings:
s = 'aababcabcdabcd'
dd = defaultdict(str)
for c in s:
dd[c]+='*'
defaultdict(<class 'str'>, {'a': '*****', 'c': '***',
'b': '****', 'd': '**'})
Use list for lists, set for sets, dict for dictionaries, and float for floats. You can use various other classes, too. The default value for integers is 0, for lists is [], for sets is set(), for dictionaries is {} and for floats is 0.0. If you would like a different default value, you can use an anonymous function like below:
dd = defaultdict(lambda:100)
Used with the code from the first example, this will produce:
defaultdict(<class 'int'>, {'a': 105, 'c': 103, 'b': 104,
'd': 102})
Exceptions
This chapter provides a brief introduction to exceptions.
Basics
If you are writing a program that someone else is going to use, you don't want it to crash if an error occurs. Say your program is doing a bunch of calculations, and at some point you have the line c=a/b. If b ever happens to be 0, you will get a division by zero error and the program will crash. Here is an example:
a = 3
b = 0
c = a/b
print('Hi there')
ZeroDivisionError: int division or modulo by zero
Once the error occurs, none of the code after c=a/b will get executed. In fact, if the user is not running the program in IDLE or some other editor, they won't even see the error. The program will just stop running and probably close.
When an error occurs, an exception is generated. You can catch this exception and allow your program to recover from the error without crashing. Here is an example:
a = 3
b = 0
try:
c=a/b
except ZeroDivisionError:
print('Calculation error')
print('Hi there')
Calculation error Hi There
Different possibilities
We can have multiple statements in the try block and also and multiple except blocks, like below:
try:
a = eval(input('Enter a number: '))
print (3/a)
except NameError:
print('Please enter a number.')
except ZeroDivisionError:
print("Can't enter 0.")
Not specifying the exception
You can leave off the name of the exception, like below:
try:
a = eval(input('Enter a number: '))
print (3/a)
except:
print('A problem occurred.')
It is generally not recommended that you do this, however, as this will catch every exception, including ones that maybe you aren't anticipating when you write the code. This will make it hard to debug your program.
Using the exception
When you catch an exception, information about the exception is stored in an Exception object. Below is an example that passes the name of the exception to the user:
try:
c = a/0
except Exception as e:
print(e)
int division or modulo by zero
Try/except/else
You can use an else clause along with try/except. Here is an example:
try:
file = open('filename.txt', 'r')
except IOError:
print('Could not open file')
else:
s = file.read()
print(s)
In this example, if filename.txt does not exist, an input/output exception called IOError is generated. On the other hand, if the file does exist, there may be certain things that we want to do with it. We can put those in the else block.
try/finally and with/as
There is one more block you can use called finally. Things in the finally block are things that must be executed whether or not an exception occurs. So even if an exception occurs and your program crashes, the statements in the finally block will be executed. One such thing is closing a file. If you just put the file closing after the try block and not in the finally block, the program would crash before getting to close the file.
f = open('filename.txt', 'w')
s = 'hi'
try:
# some code that could potentially fail goes here
finally:
f.close()
The finally block can be used along with except and else blocks. This sort of thing with files is common enough that it is has its own syntax:
s = 'hi'
with open('filename.txt') as f:
print(s, file=f)
This is an example of something called a context manager. Context managers and try/finally are mostly used in more complicated applications, like network programming.
More with exceptions
There is a lot more that can be done with exceptions. See the Python documentation for all the different types of exceptions. In fact, not all exceptions come from errors. There is even a statement called raise that you can use to raise your own exceptions. This is useful if you are writing your own classes to be used in other programs and you want to send messages, like error messages, to people who are using your class.
Bibliography
- Python documentation.
[The Python documentation is terrific. It is nicely formatted, extensive, and easy to find things.] - Lundh, Frederick. An Introduction to Tkinter.
[This is a terrific reference for Tkinter.] - Lundh, Frederick. The Python Imaging Library Handbook.
[This is a nice reference for the Python Imaging Library] - Lutz, Marc. Learning Python, 5th ed. O'Reilly Media, 2013.
[I first learned Python from the third edition. It is long, but has a lot of good information.] - Lutz, Marc. Programming Python, 4th ed. O'Reilly Media, 2011.
[This is a more advanced book. There is some good information in here, especially the Tkinter chapters.] - Beazley, Jeff. The Python Essential Reference, 4th ed. Addison-Wesley Professional, 2009.
[This is a short, but effective reference.]