Notes for Geometry
© 2022 Brian Heinold
Licensed under a Creative Commons Attribution-Noncommercial-Share Alike 4.0 Unported License
Here is a pdf version of the book.
Preface
These are notes I wrote up for my geometry class in 2021. It's an introduction to Euclid, focusing on Book I along with parts of some of the other books. The proofs generally follow Euclid's, though using modern notation and language. As appropriate, we talk about a little history and relate Euclid's work to more modern geometry.
If you see anything wrong (including typos), please send me a note at heinold@msmary.edu.
Introduction
We will be working our way through Euclid's Elements. Going through the Elements carefully is great for building proof and reasoning ability. You also really learn geometry well that way, and it can even be fun. We'll also see some of the limitations of Euclid's geometry and how that has led to some interesting ideas in modern geometry.
We don't know much about Euclid other than that he likely wrote the Elements around 300 BC. Euclid himself didn't discover all of the geometry he writes about. Much of it dates to centuries before him. Euclid's original manuscript has long since been lost. What we have now are copies of copies of still other copies, none of which are complete, and the copies differ from each other in places. But overall, we have a pretty good text of the Elements. In what follows, whenever we quote Euclid, we are quoting the English translation done by Thomas Heath in the early 20th century. It can be found at http://www.perseus.tufts.edu/hopper/text?doc=Euc.+1. Another nice online resource is D.E. Joyce's page at https://mathcs.clarku.edu/~djoyce/java/elements/.
Euclid takes what we call in modern math an axiomatic approach. He starts out by defining a few terms. Then he makes a few assumptions that he calls postulates and common notions. Modern math would call these axioms. These are a few things that are taken as given, and everything else in Euclid's geometry is built from these definitions and axioms. In any axiom system, there are always a few basic things you have to use as assumptions since it's not possible to build up a theory without starting from something. You want to keep these assumptions to a minimum and keep them as simple as possible.
Euclid's definitions
Euclid defines 23 terms in Book I. Actually, people are not sure if these were Euclid's definitions or if they were added by someone else in antiquity. For now, we will just look at a few of the definitions of terms we will need to get started with Euclid.
- A point is that which has no part. — For me, at least, this is not the most helpful definition in the world, but if you really try to define a point, you'll find it's not so easy. Euclid here is essentially saying that a point is a 0-dimensional object, an infinitely small dot.
- A line is breadthless length. — This is also not a rigorous definition. For instance, how are “length” or “breadth” defined? By “breadthless,” Euclid is saying lines have no thickness. They are infinitely thin. Note that even if point and line are not unambiguously defined, things are still okay logically. We can just take point and line as given things that may or may not represent things in the real world, and all the propositions Euclid goes on to prove are logically sound. I think with these definitions, Euclid is just trying to help us identify points and lines with real-world objects.
- The extremities of a line are points. — Euclid's lines are allowed to continue indefinitely or be finite line segments. Euclid uses the term extremities to refer to the endpoints of a line segment. In modern terminology, usually the term line is for a line that extends indefinitely in both directions, the term ray is for a part of a line that extends indefinitely in one direction but has one endpoint, and the term line segment is used for a finite piece of a line with endpoints at both ends.
- A straight line is a line which lies evenly with the points on itself. — What's the difference between a line and a straight line? By a line, Euclid means what we would now call a curve, and by a straight line, he means what we would call an ordinary (uncurved) line.
- A surface is that which has length and breadth only. — Euclid says a point has no part (no length or breadth), a line has length but no breadth, and a surface has both length and breadth. In modern terminology, he is saying that a point is 0-dimensional, a line is 1-dimensional, and a surface is 2-dimensional.
- A plane surface is a surface which lies evenly with the straight lines on itself. — Note the similarity with Definition 4. Euclid is trying to define a plane to be a flat surface as opposed to other types of curved surfaces, like the curved surfaces of a cylinder or sphere.
- A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line. — Angle is another one of those terms that we take for granted that we know from real-world experience, and it's a little tricky to put that into a formal mathematical definition. In slightly more modern terms, Euclid is saying that the angle between two lines is sort of a relationship between how the lines are sloped at the point where they meet.
- And when the lines containing the angle are straight, the angle is called rectilineal. — Except for a single case we'll see later, all the angles we will work with are rectilineal, occurring between straight lines, not between curved lines.
- When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands. — This is an important definition that will be referred to repeatedly. We usually think of a right angle as a 90° angle, but Euclid doesn't have a concept of degrees. In modern terms, the definition is saying that if two lines intersect and the angles where the lines meet are equal, then that's what a right angle is.
- A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another; — The modern way of a defining a circle is as all the points that lie at the same distance from a given point, called the center. Euclid hasn't defined a notion of distance, so he instead gives this definition involving “equal” lines that all share the same endpoint. For Euclid, a circle consists of the circumference and everything inside, though modern mathematicians use the term circle to refer just to the circumference. They use the term disc to refer to the circumference and everything inside.
Euclid's axioms
Euclid's axioms come in two types: postulates, which are geometric in nature, and common notions, which are more algebraic and logical in nature.
Postulates
- To draw a straight line from any point to any point. — In other words, given any two points, Euclid assumes it's possible to connect them with a (straight) line.
- To produce a finite straight line continuously in a straight line. — Here Euclid assumes that if we are given a line, we can extend it as far as we like.
- To describe a circle with any centre and distance. — This assumption says that we can draw any circle with a given center and radius.
- That all right angles are equal to one another. — Remember that the definition of right angles involves intersecting lines. This postulate says that no matter what lines you use, if the adjacent angles on opposite sides of one of the lines are equal, then those angles will all have the same measurement, what we would now call 90°. Euclid doesn't measure angles in degrees; instead he measures them in terms of right angles. For instance, sometimes he'll refer to what we would call a 180-degree angle as “two right angles.”
- That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles. — This is also called the parallel postulate. It is quite a bit more complicated than the other four postulates. This led people for years to see if they could prove it from the others. It wasn't until the 19th century that people finally proved that it is independent from the other postulates. The parallel postulate isn't needed until Proposition I.29, so we will postpone discussing further it until then.
The first three postulates give the existence of two famous geometrical tools: a straightedge, for drawing lines, and a compass, for drawing circles. It's important to note that neither of these have any markings to indicate distances. We aren't able to use them to measure things. The ancient Greeks and mathematicians ever since have been interested in what geometric things can be constructed using just these two tools and nothing else. We'll see in Euclid's first proposition below that they can be used to construct an equilateral triangle. With more work, it's possible to use these tools to construct other regular shapes, like squares and pentagons, though it turns out to be impossible to construct a regular heptagon (7-sided figure) using only these tools. We'll also see that we can use them to bisect an angle; that is, given an angle, we can use a straightedge and compass to construct an angle that's half as large as the original. For thousands of years people tried to find a similar construction to trisect an angle. Using techniques from abstract algebra, in the 19th century it was shown to be impossible.
Common Notions
While Euclid's postulates have a geometric nature to them, his common notions are more about numbers and logic, if we interpret them in a modern sense. There is not much in the way of numbers in Euclid. Everything is formulated in terms of geometric objects. But we can translate some of his common notions directly into modern algebraic language, though algebra was not invented until long after Euclid.
- Things which are equal to the same thing are also equal to one another. — This is a perfectly reasonable thing to assume. In algebraic notation, this says if a = c and b = c, then a = b. Namely, equality is transitive.
- If equals be added to equals, the wholes are equal. — Algebraically, this is saying if a = b and c = d, then a+c = b+d.
- If equals be subtracted from equals, the remainders are equal. — This is like #2, but with subtraction instead of addition.
- Things which coincide with one another are equal to one another. — It's not totally clear what Euclid means by this. Most people think that this notion of “coinciding” has to do with if you imagine dragging one figure onto another and having it perfectly overlap with the other. If you can do this, then this common notion says the figures must be the same in terms of lengths, angles and areas, just possibly oriented differently and located at different places.
- The whole is greater than the part. — This says that if you take a part of something, it will be smaller in measurement than the original thing. Euclid often uses this with angles, where one angle that is contained in another must be smaller than it.
Euclid's first proposition
After the definitions and axioms, Euclid moves on to using them to prove things in geometry. He builds up everything logically so that later propositions only depend on earlier propositions (and the axioms). Euclid's first proposition is about how given a line segment, we can use it along with a straightedge and compass to build an equilateral triangle, that is, a triangle with all three sides having the same length as the given segment. Here is Euclid's statement of it, followed by a modern mathematical proof.

In the proof above, we have indicated which definition/postulate/common notion we use for each statement. It gets tedious, so in future proofs we won't usually do that. Notice that one of the sentences in the proof, “Let C be the point where the two circles meet,” has no justification. While it seems obvious from the pictures, how do we know the two circles really do meet? We actually don't. That's a well-known gap in Euclid's axioms. There's nothing in them that says that the two circles must intersect. We would need some sort of continuity assumption that says that lines and circles are continuous and unbroken, without any gaps in them. But that's actually a fairly sophisticated concept that doesn't show up in modern math until courses in real analysis.
A quick note on proving things: In many proofs, there is often a clever trick that needs to be found. In this case, that trick is to draw circles at A and B, both with radius AB, and to look at the intersection. Once we have done that, a little reasoning finishes out the proof. What's nice about this proposition is, since it's the first one, there isn't a whole lot to work with other than segment AB, a straightedge, and a compass. Those circles we drew are really the only thing we could do to start. Once we have more tools at our disposal, it will be tricky to decide which is the right one for the job.
For contrast with our modern proof, here is Euclid's proof (from the Heath translation):
Let AB be the given finite straight line.Thus it is required to construct an equilateral triangle on the straight line AB.
With centre A and distance AB let the circle BCD be described; [Post. 3] again, with centre B and distance BA let the circle ACE be described; [Post. 3] and from the point C, in which the circles cut one another, to the points A, B let the straight lines CA, CB be joined. [Post. 1]
Now, since the point A is the centre of the circle CDB, AC is equal to AB. [Def. 15]
Again, since the point B is the centre of the circle CAE, BC is equal to BA. [Def. 15]
But CA was also proved equal to AB; therefore each of the straight lines CA, CB is equal to AB.
And things which are equal to the same thing are also equal to one another; [C.N. 1] therefore CA is also equal to CB.
Therefore the three straight lines CA, AB, BC are equal to one another.
Therefore the triangle ABC is equilateral; and it has been constructed on the given finite straight line AB.
(Being) what it was required to do.
It's quite a bit longer and wordier than our modern proof. Part of it is that Euclid always follows a particular structure in his proofs where he starts by saying what he is going to prove and finishes by saying it again. Modern proofs don't include these features. Also, Euclid's use of language is a bit wordier and less efficient than what modern mathematicians use. After you read enough of his proofs, you start to get used to his way of writing, but it takes awhile. Most of the proofs we will give in these notes will be based on Euclid's original proofs, but using more a modern style.
As can be seen above, Euclid describes the circle with center A and radius AB as circle BCD. In modern terminology, we usually specify a circle by it's center and radius. Euclid specifies it here by 3 points on the circle itself. The points D and E on the circles don't play any role in the proof other than in naming the two circles.
Propositions I.2 and I.3
Euclid here is showing that if we have a point and a line, we can use a straightedge and compass to make a copy of the line at the point. Note that the copy won't necessarily face the same direction as the original, but it will have the same length.

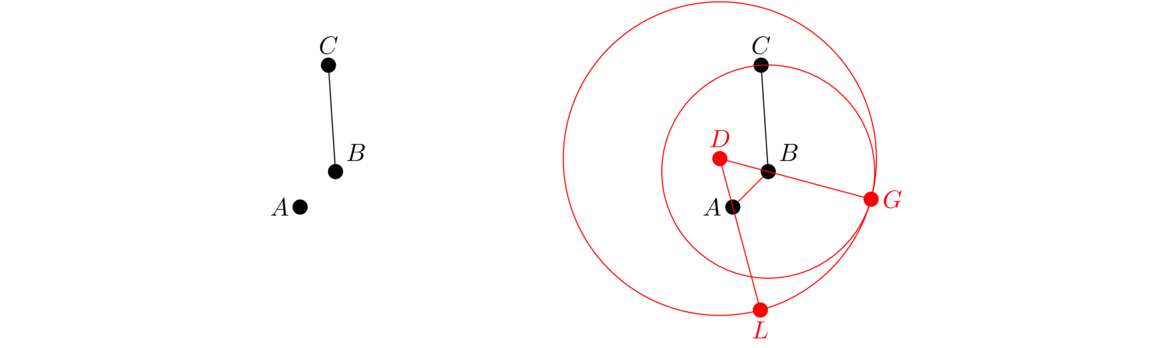
Our goal is to show that AL is the line we want, namely that it equals BC. To see this, first note that DG = DL because both are radii of the big circle, and AD = BD because both are sides of the same equilateral triangle. So the lines DL and DG are equal, and if we remove the equal segments AD and BD from each one, respectively, the pieces that are left are equal. That is, AL = BG. But BG = BC since both are radii of the smaller circle, so AL = BC, as desired.
You might wonder why we chose letters like G and L instead of E and F. In Euclid's proof, he used those letters in describing some of the lines and circles he drew, but in our proof, we don't really need them, so we left them out. But it would be good if the letters in our figures match those in Euclid's, so while we may leave out some letters, what's left will match what Euclid has.
Proposition I.2 allows us to a copy a length, but it doesn't allow us any control over how the copy is oriented. This proposition allows that. In particular, it says that given the lines AB and C, shown below on the left, we can mark off a point on AB that it is equal to C in length.

This proposition is used a lot to take a length somewhere in a figure and transfer it somewhere else. Remember that Euclid's straightedge is not a ruler. It doesn't have markings. The compass doesn't either. People usually describe Euclid's compass as collapsible, in that once you pick it up, it forgets what radius it was set to. Proposition I.3 essentially says that we can treat the compass as if it were rigid, that we can set it at two points in a figure and have it maintain that length while we pick the compass up and move it elsewhere.
Notice how Euclid uses the phrase “to cut off.” There is not much of what we would think of as arithmetic in Euclid, adding and subtracting numbers. This proposition gives the geometric equivalent of subtraction, namely subtracting a line segment from another. When we cut off AE from AB, we are left with EB. Proposition I.2, on the other hand, is about adding segments together, as it allows us to place one segment at the end of another.
Propositions I.4 to I.8
There are a lot of words here. Euclid is saying if we have two triangles that agree in two sides and the angle between them, then the third sides of each as well as the other two angles will match up between the triangles. In modern terms, we would say the triangles are congruent. They are equal in all their measurements, though they may be located in different places and oriented differently. We will sometimes use the symbol ≅ to indicate two triangles are congruent. You might remember this proposition from high school geometry as Side-Angle-Side or SAS.

Note on notation: In figures like the one above, we will use markings on segments and angles to indicate they are equal. Sometimes, we'll use double or triple markings if there are multiple different groups of things that are equal.
This proof illustrates another gap in Euclid's logic. There is no axiom that allows us to move one object onto another like this. Common Notion 4 is close, but it isn't quite enough. For instance, how do we know the figure will not be deformed by being moved? It seems like this proof technique was in use quite a bit by Greek geometers, though Euclid seems to have avoided using it as much as he could. He must not have been able to come up with a proof for Proposition I.4 that didn't use it. The mathematician David Hilbert, who came up with a completely rigorous formulation of geometry in the late 1800s, had 20 axioms, as opposed to Euclid's 10, and one of those axioms is SAS.
SAS is used quite a bit. It's a particularly useful technique for showing that two angles or line segments are equal. We do this by finding two triangles that contain them and then showing that the triangles are congruent using SAS.
An isosceles triangle is one in which two of the sides are equal. This proposition says that in an isosceles triangle the angles at the base (the angles opposite the two equal sides) are equal. Further, the angles beneath them are equal, too. The angles are supplementary, so we would expect them to be equal if the base angles are equal, but Euclid hasn't established anything about supplementary angles yet, so we can't use that fact here. This proposition is very useful, especially the part about the angles within the triangle being equal.

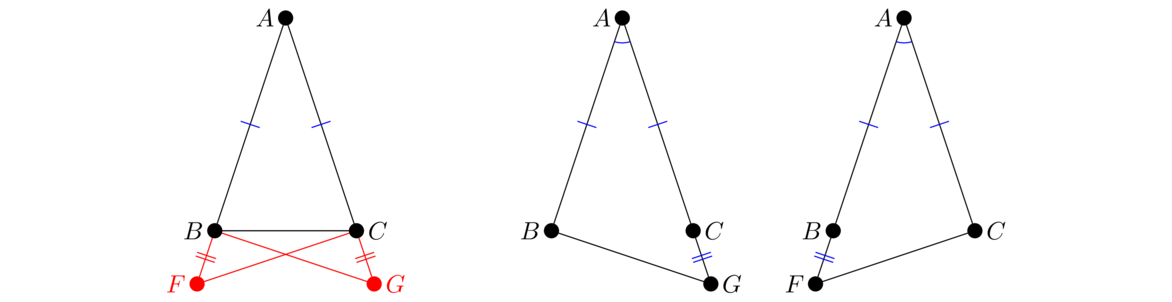
Next, look at △BFC and △CBG. We have ∠F = ∠G, BF = CG, and BG = CF, so by SAS, those triangles are congruent. Therefore, ∠CBF = ∠BCG, which is the second thing we are supposed to prove. Finally, to show that ∠ABC = ∠ACB, note that we already know ∠ABG = ∠ACF, and the congruence we just found tells us that ∠CBG = ∠BCF. So the parts that are left over in each angle, ∠ABC and ∠ACB, must be equal.

This is probably Euclid's most involved proof so far. There is a much shorter proof that the base angles are equal, which is attributed to the Greek mathematician Proclus in the 5th century. He says to think about △ABC in two ways: as itself and as △ACB, like below. By SAS, they are congruent, which means ∠B = ∠C.
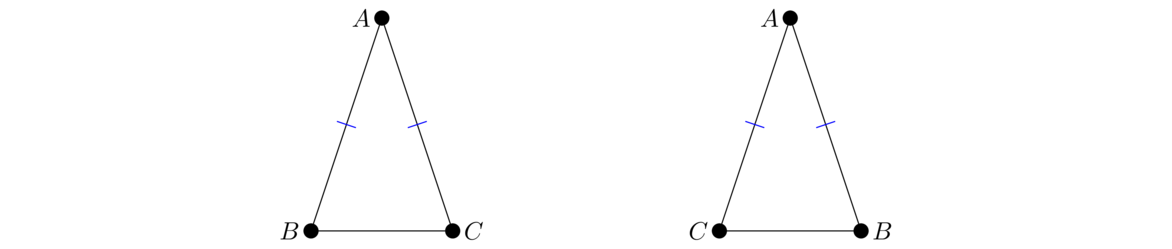
Note about notation: We use the symbol ∠ to refer to an angle. Usually an angle is specified by three vertices, and there are always multiple possible names. For instance ∠ABC is the same as ∠CBA. If there is only one angle shown in a figure at a certain point B, then we will sometimes just say ∠B for simplicity.
This is a converse to I.5. Recall that if you have a statement A → B, the converse is B → A. The converse of a statement is not always true. For instance, if it's snowing, then it must be cold, but if you flip that around into if it's cold then it's snowing, you get something that's not necessarily true. However, sometimes the converse is true, like here. When a converse of a statement is true, Euclid will often prove it right after the original statement.
To prove this proposition, Euclid uses a proof by contradiction. This is one of the most useful proof techniques. To do one, you start by assuming the opposite of the statement what you want to prove. Then, you logically reason through some stuff and eventually arrive at a statement that's clearly false. That means your assumption must be wrong, meaning the original statement must be true (since it being false leads to something bad).
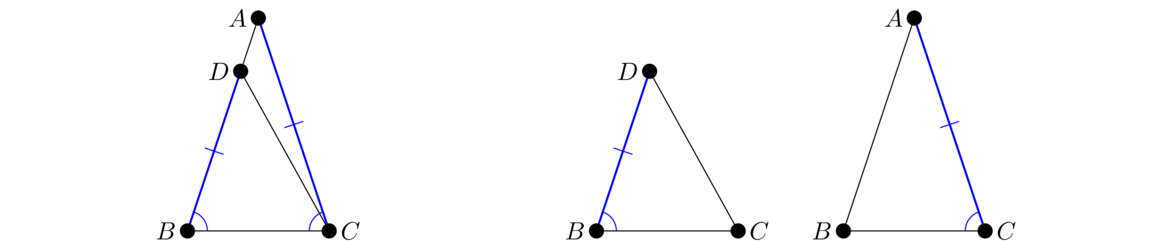
Notice in the proof above, we use the phrase “without loss of generality” in assuming that AB is larger than AC. The idea is that one of them must be larger, and, whichever one it is, the proof is essentially the same, just with the names changed. To be fully rigorous, we would have to do both cases, but that's tedious since the other case is the exact same argument. So we just pick one to be larger and do that case. This is common in math proofs.
It might take a few reads before it's clear what this is saying. It says first to take a line as the base of a triangle, and join two lines from its endpoints meeting at a point, forming a triangle. If you try to do that again with two news lines of the same lengths as the first set of lines, there is no other way they could both meet at a different point. In other words, once you fix the base of a triangle and choose lengths for its other sides, there is only one possible triangle that can be formed.

In the proof above, we assume D lies outside of △ABC. But it could also lie inside. In that case, the proof would be similar, but a little different. Euclid doesn't handle this case. He often will do this, where he will just give one case, usually the most difficult case, and leave the others to the reader.
Proposition I.7 is not used anywhere except to prove Proposition I.8.
This is another congruence criterion, Side-Side-Side (SSS). That is, if two triangles agree in all three sides, then they are congruent. The proof relies on the same superposition idea as I.4, which makes it a little fishy for the same reasons as mentioned earlier.
Propositions I.9 to I.12
Propositions I.9 to I.12 are all similar constructions, two about bisecting things and two about perpendicular lines.
This is a pretty straightforward statement. Remember that Euclid uses the term rectilinear angle in the same way that we use the term angle. It's an angle where the sides are straight. Euclid allows angles with curved sides, which is why you'll usually see him use the term rectilinear angle when he's talking about ordinary (non-curvy) angles.
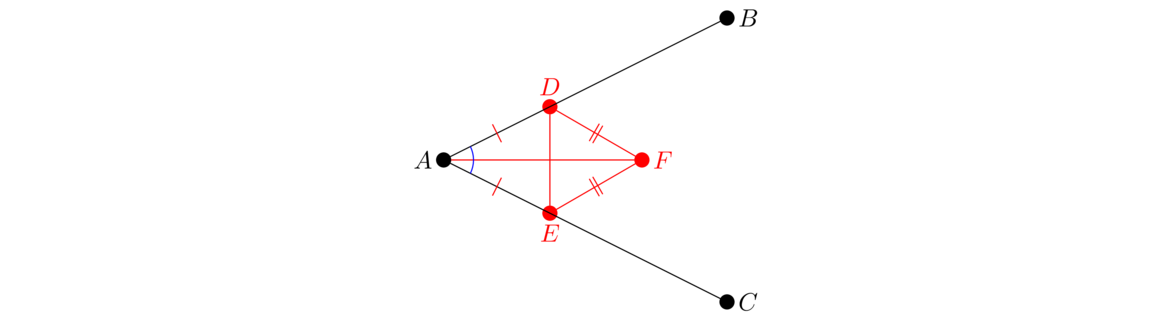
To see why, consider the triangles △ADF and △AEF. They both share side AF. Further, DF = EF since those are sides of the same equilateral triangle, and AD = AE by how point E was defined. Therefore, by SSS, the triangles are congruent, meaning ∠DAF = ∠EAF. Thus, we have bisected ∠BAC.
Notice also that since the two triangles are congruent, ∠ADC = ∠BDC. Recall Euclid's definition of a right angle involves two lines meeting and the angles being the same on either side. So both these angles are right angles, meaning this bisector is perpendicular to the line being bisected. Euclid's next proposition is proved by a really similar argument to this.
Let AB be the given line and let C be a point on it. We want to draw a line perpendicular to AB that meets it at C. We would like to do something similar to the proof of the previous proposition, but C might not lie in the middle of AB. To fix that, pick a random point D between A and C, and mark off E at the same distance to C as D is, but between C and B. Then use Proposition I.1 to create an equilateral triangle △DEF, and connect FC.

We claim that FC is the line we want. By the definition of right angles (Definition 10), we would need to show that ∠DCF = ∠ECF. Look at △CDF and △CEF. They both share side CF, they have DF = EF since those are sides of the same equilateral triangle, and CD = CE by how E was defined. So by SSS, the triangles are congruent, making ∠DCF = ∠ECF, meaning they are both right angles.
This proposition is similar to the previous one, except now we don't need point C to be on the line.
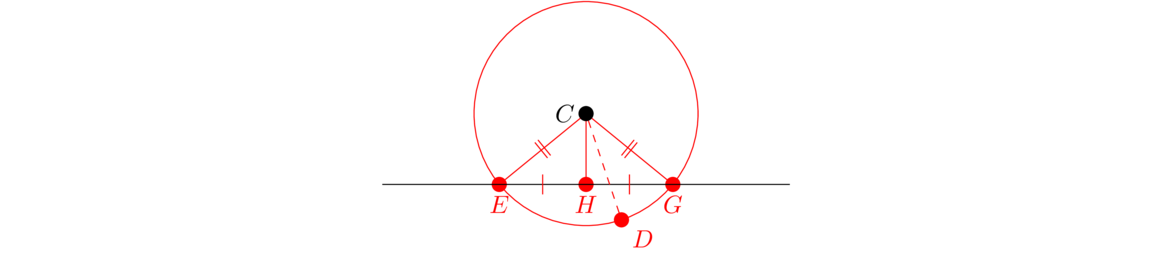
We claim that ∠CHE = ∠CHG, making both right angles. We can show this by looking at △CHE and △CHG. They both share CH, they have CE = CH since both are radii of the same circle, and EH = GH since H was constructed to be midway between E and G. Thus, by SSS the two triangles are congruent, making ∠CHE = ∠CHG.
There is a bit of a gap in this proof. How do we know the circle hits the line? As we noted after Proposition I.1, we would need some sort of continuity axiom. Assuming that, how do we know for sure that it hits in two places? Euclid does cover this, but not until Book III.
One important thing to remember about these four propositions are that they are recipes for how to bisect angles and lines and how to draw perpendiculars, but they cannot be used to show an already existing line is a bisector or a perpendicular. If you want to show that a given line bisects something or that it is perpendicular to something, you would need to use something else, such as SAS or SSS.
Propositions I.13 to I.19
The proposition says that two angles on either side of a line intersecting with another will add up to 180°. That is, they are supplementary. In the figure above on the left, it says that α+β = 180°. Euclid only measures angles in terms of how many right angles they are, so when he says “two right angles” that is what we would call 180°. Below, we have a proof that is based on Euclid's, but written in modern algebraic terms.

Here is a snippet of Euclid's actual proof: “Then, since the angle CBE is equal to the two angles CBA, ABE, let the angle EBD be added to each; therefore the angles CBE, EBD are equal to the three angles CBA, ABE, EBD.” If you look hard enough, you'll see this is equivalent to what we did above. In particular, what Euclid is doing here is a lot like adding the same thing to both sides of an equation in algebra. But Euclid didn't have algebra. In fact, most of mathematics was done in this verbal way until the Renaissance.
This proposition is the converse of the previous one. That proposition says that when two straight lines meet, the angles will add up to 180°. This one says that if the angles add up to 180°, then the segments at the base of the angles must form a straight line, not something crooked.

Euclid's proof is slightly different from the one above. His is a proof by contradiction which shows that β+γ = β, which is impossible by Common Notion 5, as one angle is contained in the other.
When two lines intersect, the angles opposite each other are called vertical angles. This proposition says they are always equal. In the figure below, the proposition tells us that α = γ and β = δ.
Our proof below is based on Euclid's, but is updated to use some algebra.

This useful proposition is sometimes called the exterior angle theorem. The angle on the outside of the triangle created by producing (extending) one of the sides is called an exterior angle. It is the angle γ in the figure below on the left. The proposition says that γ > α and γ > β. Note that γ is not necessarily bigger than the other angle in the triangle. If γ were an acute angle, for instance, then the angle next to it in the triangle would be greater than it.

Start by using Proposition I.10 to bisect side AC at a point E. Connect BE and then extend this using Proposition I.3 to a point F such that BE = EF. Connect FC. We claim that △AEB≅ △CEF. We know this is true because AE = EC since AC is bisected at E, BE = EF by how F is defined, and ∠AEB = ∠FEC by I.15 since they are vertical angles. So by SAS, the triangles are congruent. This means that α = ∠ECF. But ∠ECF is contained in γ, so we have γ > α. To prove γ > β, we would repeat the process but start by bisecting BC instead of AC and use the vertical angle on the opposite side of C from γ.
You probably remember from grade school that the angles in a triangle sum to 180°. Euclid will eventually prove this, but not until Proposition I.32. That proposition cannot be proved without using Postulate 5, the parallel postulate. Euclid is trying to see how far he can get without using it. And here, Euclid shows that without using the parallel postulate we can at least show that the sum of any two angles in a triangle is less than 180°.

The next two propositions go together:
Referring to the figure below on the left, Proposition I.18 says if b > a, then β > α, and Proposition I.19 says if β > α, then b > a. In other words, in a triangle longer sides correspond to longer opposite angles and longer angles open up to longer sides.

For I.18, our hypothesis is b > a. We want to show that β > α. Since b > a, we can use Proposition I.3 to mark off a point D on AC such that AD = AB. This makes △ABD isosceles, so by Proposition I.5, the angles at the base are equal, namely ∠ABD = ∠ADB. Let γ = ∠ABD. Then γ is exterior to triangle △BCD so γ > α by Proposition I.16. However, γ is contained in β, so we must also have β > α, as desired.
For I.19, our hypothesis is β > α. For the sake of contradiction, suppose a ≤ b. There are two cases: a = b or a < b. If a = b, then by Proposition I.5, we must have α = β, which contradict our hypothesis. And if a < b, then by Proposition I.18, α < β, which also contradicts our hypothesis.
Most of the propositions in this section are used quite a bit, especially I.13 (supplementary angles) and I.15 (vertical angles).
Propositions I.20 to I.26
This proposition is known as the triangle inequality. It gives a criterion for when a triangle can be built from various sides. Namely, if it ever happens that two values add up to a value less than a third value, then we can't make a triangle out of them. For instance, we can't make a triangle out of sides of length 1, 1, and 3 since 1+1 < 3. The quick way to use the proposition is that if the sum of the smallest two length is less than the largest length, then there can't exist a triangle with sides of those lengths.
This statement is also a partial proof of the fact that the shortest distance between two points is a straight line. Namely, if instead of going via a straight line, we take a two-step path (along the sides of a triangle), then that path must be longer than the straight-line path along the hypotenuse. It's a partial proof because it doesn't handle curved paths. To do that requires some more sophisticated math, namely something called calculus of variations.
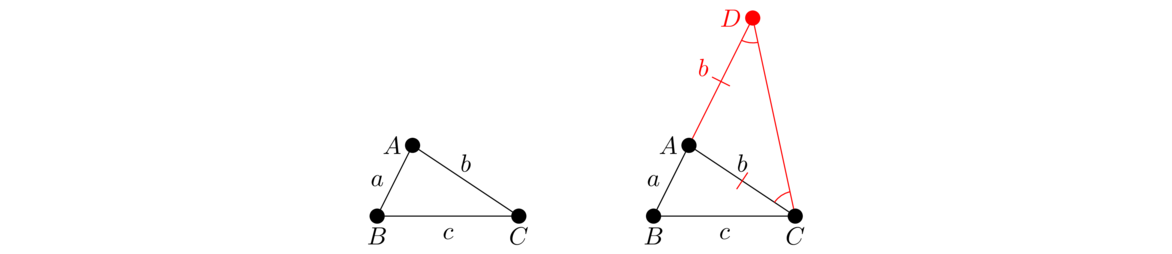

It might take a few reads to understand the proposition. We start with △ABC and build a new triangle on the same base BC but with a new apex inside of the old triangle. One part of the proposition says that the angle at the top of the new triangle will be greater than the angle at the top of the original triangle. That is, ∠D > ∠A in the figure above. It might help to try to picture an extreme case with D just barely above BC; in that case ∠D will be almost 180°. The other part of the proposition says that the sides of the new triangle will have a total length less than the sides of the original, which makes sense since they have less distance to go.
We'll prove the part about the angles first. Let α = ∠A, β = ∠CED, γ = ∠D. Notice that γ is exterior to △CDE, so γ > β by Proposition I.16. And notice that β is exterior to △ABE, so by Proposition I.16 again, β > α. Putting this all together, γ > α, which is what we want to prove.
Next we'll prove AB+AC > DB+DC. Start by applying the triangle inequality (Proposition I.20) to △ABE to get AB+AE > BE. Then add EC to both sides of this expression to get AB+AE+EC > BE+EC. And notice that AE+EC=AC, so AB+AC > BE+EC. Next, we'll do something similar with △CDE. By the triangle inequality, DE+EC > DC. Add BD to both sides to get BD+DE+EC > DB+DC. Since BD+DE = BE, this becomes BE+EC > DB+DC. Putting this together with the inequality from △ABE gives AB+AC > DB+DC, which is what we want.
Recall that Proposition I.20 says if a, b, and c are any three sides of a triangle, then a+b > c. This is a necessary condition for a triangle to exist. It's often used in its contrapositive form, namely that if we have values a, b, and c, satisfying a+b ≤ c, then we can't form a triangle out of them. Proposition I.22 says that the a+b > c condition is also sufficient. That is, if three lengths satisfy the condition, then we can indeed create a triangle out of them. We can then say that the triangle inequality is a necessary and sufficient condition for a triangle to exist or that a triangle exists if and only if its sides satisfy the triangle inequality.
In math, sometimes a condition will only be necessary and not sufficient. For instance, ending in 2, 3, 5, 7, or 9 is a necessary condition for a number to be prime. Every prime ends in one of those digits. But it's not sufficient since there are numbers ending in those digits that are not prime. Sometimes a condition will be sufficient but not necessary. For instance, ending in 5 is a sufficient condition for a number to be divisible by 5, but it's not necessary as there are other ways for a number to be divisible by 5. Sometimes we get lucky, as with the triangle inequality, getting a nice condition that is both necessary and sufficient.

The above is a modern rendering of Euclid's proof. Notice the similarity to the proof of Proposition I.1 (creating an equilateral triangle), which also relies on intersecting two circles. Like that proof, this one has a gap. How do we know those two circles intersect? In particular, why is it that those circles will intersect whenever the triangle inequality is satisfied but not when it isn't? It would be nice if Euclid addressed this. You can try the construction for yourself with values that don't satisfy the triangle inequality and watch how the triangles end up missing each other, either because one ends up inside the other or because there is a gap between them.
Note also that the proof shows we can base the triangle on any line we want.
This proposition says that we can transfer angles. We can think about having a protractor that we can set to match an angle somewhere in a figure and use it to transfer that angle elsewhere in a figure. This is similar to how we can use Proposition I.3 to transfer lengths.

For these two propositions, consider the triangles below that are equal to each other in two sides. Proposition I.24 says if b > a then β > α. Proposition I.25 is the converse of Proposition I.24, namely that if β > α, then b > a. We'll prove both of them together. Most of the work goes into proving the first one.

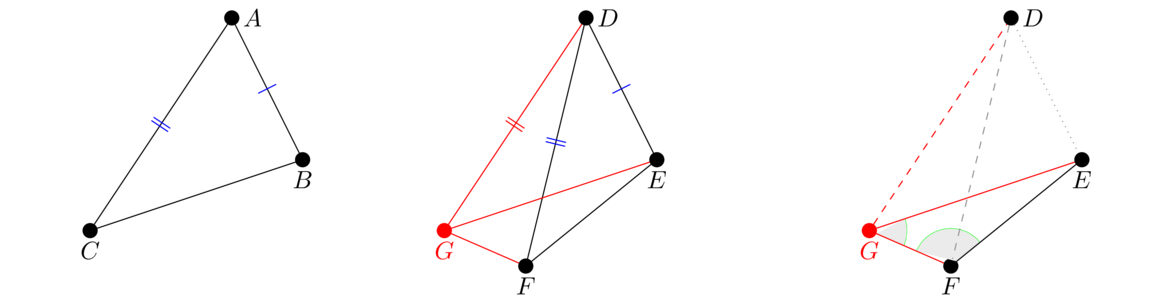
Our goal is to show that BC > EF. The congruence above shows that BC = EG, so it suffices to show that EG > EF. Since EG and EF are part of the same triangle, by Proposition I.19 if we can show that the angle opposite EG is greater than the angle opposite EF, then we will have EG > EF. So we need to show ∠EFG > ∠EGF. To do this, note first that since △DFG is isosceles, by Proposition I.5 we have ∠DGF = ∠DFG. So we have that ∠EFG contains ∠DFG, ∠DFG = ∠DGF, and ∠DGF contains ∠EGF. Thus ∠EFG > ∠EGF as desired. The figure above on the right might help in seeing this.
To prove Proposition I.25, we use a proof by contradiction. Our hypothesis is that BC > EF. Suppose it were not true that ∠A > ∠D. There are two possibilities: First, we could have ∠A = ∠D. If so, then △ABC≅ △DEF by SAS since AC = DF, ∠A = ∠D, and AB = DE. But this would mean BC = EF, which contradicts our hypothesis. Second, we could have ∠A < ∠D. But then by Proposition I.24, we would have BC < EF, which again contradicts our hypothesis.
Notice that the proof of Proposition I.25 relies on the proof of Proposition I.24. Euclid often does this, where he uses A → B in proving the reverse implication, B → A. Modern mathematicians would often prove both at the same time using a string of equivalencies.
This proposition consists of the two useful congruence criteria, ASA and AAS. Combined, they say that if two triangles share any two angles and any one side, then they must be congruent.
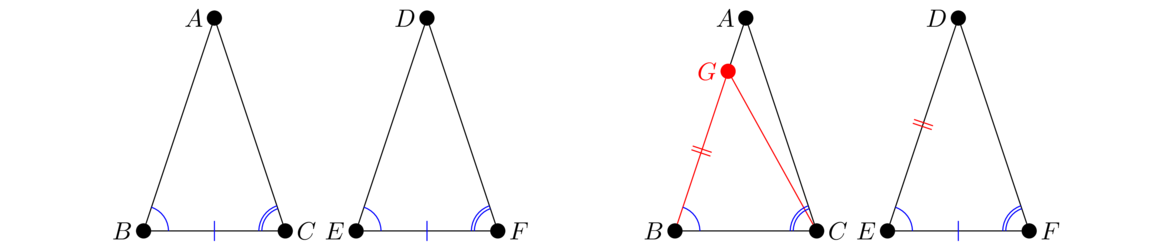
For the AAS proof, we would assume ∠B = ∠E, ∠C = ∠F, and AB = DE. We would then start by showing BC = EF using a contradiction proof similar to above, making use of SAS and also Proposition I.16.
The four congruence criteria we have are SAS, SSS, ASA, and AAS. The other possible criteria are AAA and SSA, but neither of those actually works. It's possible to come up with triangles that satisfy those but aren't congruent. However, SSA does work in a particular special case, namely when the angle in question is right or obtuse.
Propositions I.27 to I.33
The propositions in this section are about parallel lines. Here is Euclid's Definition 23, concerning parallel lines:
Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.In other words, parallel lines are lines that don't intersect. The notation ℓ ∥ m is used to indicate that lines ℓ and m are parallel. The next several propositions will involve one line (called a transversal) intersecting two lines, like in the figure below. The four angles on the outside of the intersection are called exterior angles. They are ∠AGE, ∠BGE, ∠CHF, and ∠DHF. The four angles on the inside are called interior angles. They are ∠AGH, ∠BGH, ∠CHG, and ∠DHG. Further, the pairs ∠AGH and ∠DHG, as well a ∠BGH and ∠CHG, are called alternating interior angles. The two angles in a pair of alternating interior angles lie on opposite sides of the transversal. Both sets of alternate interior angles are shown below on the middle and right.

This says that if we have a picture like below on the left where a line intersecting two other lines makes the indicated angles equal, then the lines must be parallel.

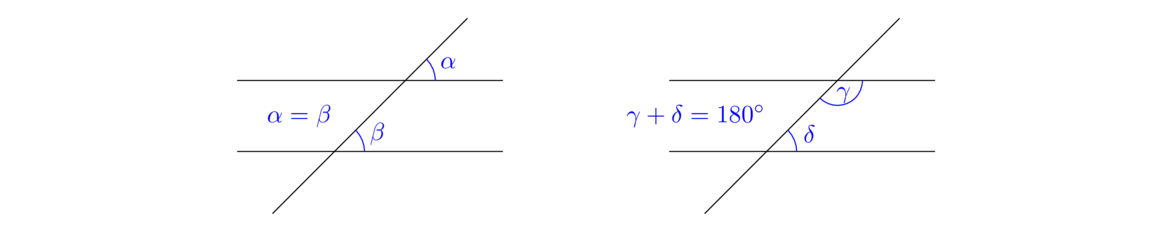
The proposition says two things: (1) if α = β as in the figure above on the left, then the lines are parallel, and (2) if γ+δ = 180° as in the figure above on the right, then the lines are parallel. The proof of each relies on showing that if either of these conditions is satisfied, then the alternate interior angles are equal, so the lines are parallel by Proposition I.27.
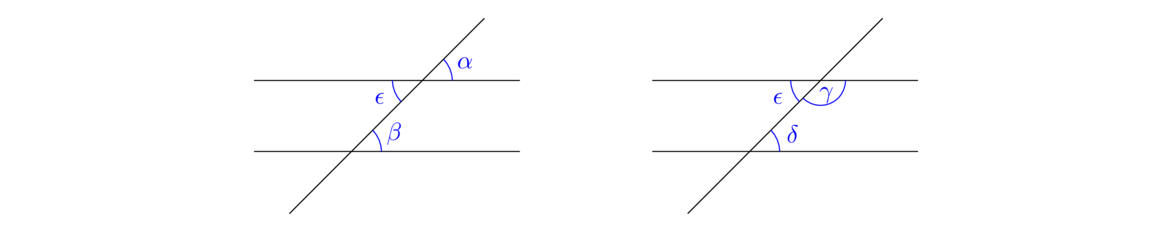
Next assume γ+δ = 180° as in the figure above on the right. By Proposition I.13, γ+ε = 180°. And we are given that γ+δ = 180°. Putting these equations together tells us that ε = δ, meaning the alternate interior angles are equal. So by Proposition I.27, the lines are parallel.
Propositions I.27 and I.28 are the main tools in Euclidean geometry for showing that lines are parallel. They give us three closely related conditions we can choose from. The next proposition is the converse these propositions. It says if the lines are parallel in the figures below, then all three of the indicated conditions about various angles are true.
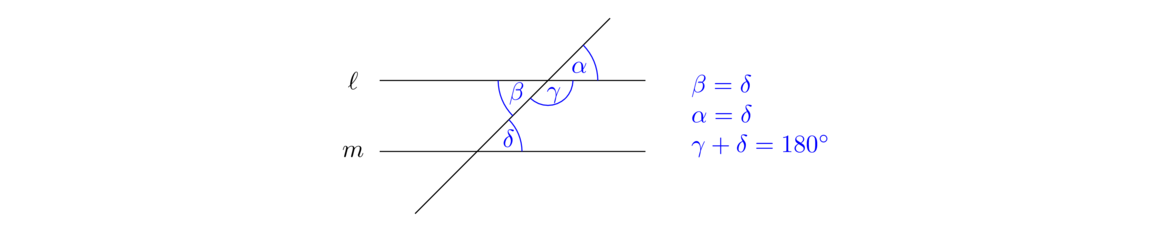
This is the first proposition of Euclid's whose proof requires Postulate 5, the parallel postulate. It seems like Euclid tried to get as far as he could without using it, and at this point he finally does need it. Here is the statement of the parallel postulate:
That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
In other words, it says if we have a figure like the one above in which γ+δ < 180°, then the lines must not actually be parallel and must intersect somewhere.
Statements (2) and (3) follow quickly now that we have proved (1). For (2), note that α = β by Proposition I.15, and since β = δ, we therefore have α = δ. For (3), by Proposition I.13, we have γ+β = 180°, and plugging in δ = β gives γ+δ = 180°.
In symbols, this says if ℓ ∥ m and m ∥ n, then ℓ ∥ m. In other words, being parallel is a transitive relation.
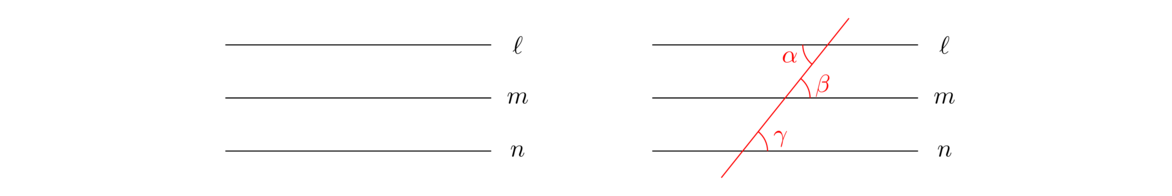

This proposition is a construction about how to create a line parallel to another. The proof above relies on Proposition I.23, which allows us to transfer angles. An alternate proof would be to use Propositions I.11 and I.12 to draw two perpendicular lines, which would result in a new line parallel to the original.
The second part of the statement of this proposition is a fact you've probably known for a long time: the angles in a triangle always sum to 180°. It's taken Euclid this long to build up enough machinery to finally prove it.

Since EC is parallel to AB, the alternate interior angles ε and α are equal by Proposition I.29. That proposition also tells us the angle θ, exterior to the parallel lines, equals β. So ε = α and θ = β, so δ = ε+θ = α+β, which is one part of what we want to prove. For the other part, note that by Proposition I.13, we have γ+ε+θ = 180°, and plugging in ε = α and θ = β gives α+β+γ = 180 ∘ .
The proof relies on Proposition I.29, which in turn relies on the parallel postulate. It can be shown that Proposition I.32 cannot be proved without the parallel postulate, or something equivalent to it. Note that this proposition is a generalization of Proposition I.17, which says that any two angles sum to less than 180°. It's also a generalization of Proposition I.16, which says that the exterior angle δ is greater than both α and β. This proposition says that, in fact, δ = α+β. Both parts of this proposition are used extensively by Euclid.
This proposition is another handy tool for showing lines are parallel. It says that if you start with two equal and parallel lines, AB and CD, shown in the figure below, then AC and BD will be equal and parallel as well.

Euclid's ten axioms consist of his five postulates and five common notions. They are all pretty simple and self-evident facts, things that most people are happy to take for granted, with the exception of the parallel postulate. Its statement is considerably more complex than the others. It just looks like it should be a proposition, not something we take as given. For that reason, people for thousands of years tried to prove it from the other axioms. No one could because it really is independent of those other axioms, though it took until the 19th century to prove that.
Over the years, people have come up with a number of statements which are logically equivalent to the parallel postulate. When we say logically equivalent, we mean that A and B are logically equivalent if A implies B and B implies A. We could take any of these equivalent statements as our axiom in place of the fifth postulate, and nothing would change in terms of what we could and couldn't prove in Euclidean geometry.
For instance, one such statement is Proclus' Axiom, which states that if a line intersects one line of a pair of parallel lines, then it must intersect the other. We can use Proclus' Axiom to prove the parallel postulate and we could use the parallel postulate to prove Proclus' Axiom. Thus, we could take Proclus' Axiom as given and use it to prove everything in Euclid that needs the parallel postulate. Wikipedia has a nice list of things that are equivalent to the parallel postulate at https://en.wikipedia.org/wiki/Parallel_postulate. Here are a few interesting ones:
- Proclus' Axiom — If a line intersects one line of a pair of parallel lines, then it must intersect the other.
- Playfair's Axiom — Given a line and a point not on the line, we can draw at most one line parallel to the given line that passes through the point.
- The sum of the angles in any triangle is 180°.
- Rectangles exist.
- Proposition I.30 — Straight lines parallel to the same straight line are also parallel to one another.
- Wallis's Axiom — Triangles can be made arbitrarily large.
Some of these are downright surprising. As the Wiki page notes, a lot of the people that tried to prove the parallel postulate from Euclid's other axioms implicitly used some of these statements, not realizing that the statements themselves don't follow from Euclid's axioms and would need to be axioms themselves if they are to be used.
Of all of these, perhaps the most interesting is Playfair's Axiom about how at most one line can be drawn parallel to a given line through a given point not on the line. Recall that Proposition I.31, which does not rely on the parallel postulate, shows that there is at least one line. So combining this statement and Playfair's Axiom, there is exactly one parallel line we can draw. In the 19th century mathematicians started asking what if you pretended that the Playfair's Axiom was not true, namely that we either couldn't draw any lines parallel to a given line or that we could draw more than one line parallel. This results in different types of geometries, now called elliptic geometry and hyperbolic geometry. These geometries have some similarities with ordinary Euclidean geometry and some notable differences.
Elliptical geometry is closely related to spherical geometry, which has a lot of practical uses given that we live on a sphere. In spherical geometry, lines are what are called great circles. The earth's equator is an example of a great circle. With lines on a sphere being great circles, it turns out that there are no parallel lines, period, as any two great circles must intersect somewhere. Spherical and elliptical geometry have other interesting features, such as the fact the sum of the angles in a spherical triangle will always be more than 180°. In hyperbolic geometry, the situation is somewhat reversed, as there are infinitely many lines parallel to a given line through a given point and the sum of the angles in a hyperbolic triangle are always less than 180°. Hyperbolic geometry is also practical, at least for physicists, since it is speculated that the universe itself is hyperbolic.
In summary, in the 19th century, mathematicians decided to take a “what if we pretended the parallel postulate is not true” approach and developed some interesting new mathematics, now called non-Euclidean geometry. Euclid himself seems to have realized that the parallel postulate is something special, as he try to avoid using it as long as he could. The parts of Euclid's geometry that don't rely on the parallel postulate are sometimes called neutral geometry or absolute geometry. The parts of Book I that belong to neutral geometry are Propositions I.1 through I.28 and also I.31.
Propositions I.34 to I.41
This section of propositions is all about areas. We won't attempt a formal definition of area here. Intuitively, area is how much 2-dimensional space something takes up. It's similar to how length is how much 1-dimensional space something takes up, and volume is how much 3-dimensional space something takes up.

A parallelogram is a four-sided figure with opposite sides being parallel. In particular, in parallelogram ABCD, we have AB ∥ CD and AC ∥ BD. Proposition I.34 says that in any parallelogram, the opposite, parallel sides are equal to each other, and the angles on opposite corners are equal as well, as indicated above in the middle. It also says that both diameters, which are lines connecting opposite corners, divide the parallelogram into triangles with equal areas.
In this proposition, Euclid is referring to a figure like the one below, where the two shaded parallelograms share the same base and are “in the same parallels.” This part about parallels means that the bases of the two parallelograms both sit on one line of a pair of parallel lines and their tops both sit on the other line. In modern terms, we would say the parallelograms have the same height, but Euclid always uses this “same parallels” terminology. Note also that Euclid uses the term equal here to mean that the parallelograms have equal area, not that they are congruent to one another. It's possible for two figures to have equal areas and not be congruent to each other.

The proposition says that the two parallelograms will have the same area, no matter where along the upper line their tops are moved to. As the top is moved farther from the base, the parallelogram will stretch out to become long and thin, but its area remains the same. To me, at least, this is a little surprising. But looking at it with modern eyes, this proposition is simply saying that the area of a parallelogram is proportional to its base times its height. You might remember from grade school the area formula A = bh for a parallelogram.

Now let G be the intersection point of DC and BE. If we take △ABE, subtract away △DGE and add in △GBC, the area that is left is parallelogram ABCD. Likewise, if we start with △DCF, subtract away △DGE and add in △GBC, the area that is left is parallelogram EBCF. In both cases, we are start with triangles with equal areas, subtract off △DEG and then add in △GBC. So resulting areas, the parallelograms, should be equal.
In the proof above, we have drawn the parallelograms in such a way that AD and EF don't overlap. But it's possible they do. In that case, the proof above works similarly, but a few things change, such as the fact that △DGE and △GBC disappear. Euclid himself doesn't consider this case. As mentioned earlier, he often proves only the trickiest case and leaves the others as exercises for the reader.

This is similar to the previous proposition, except now the bases don't have to be in the same place. They can be anywhere on the bottom parallel line.
Let the parallelograms be ABCD and EFGH. Note that BC = FG by hypothesis, and FG = EH by Proposition I.34, so BC = EH. Connect B to E and C to H. This creates the four-sided figure EBCH. The lines just drawn connect sides BC and EH, which are equal and parallel, making the new lines equal and parallel as well by Proposition I.33. Thus, EBCH is a parallelogram. It shares base BC with ABCD, so by Proposition I.35, they both have the same area. It also shares its top, EH, with EFGH, so by Proposition I.35 again (treating the top as a “base”), they both have the same area. Thus, all three parallelograms have the same area, which proves this proposition.

These two propositions are just like Propositions I.35 and I.36 except they are for triangles instead of parallelograms. Euclid's proofs of I.37 and I.38 are essentially the same, so we will just prove I.38 here, since I.37 is just a special case of I.38.

These two propositions are converses to Propositions I.37 and I.38. Proposition I.40 is interesting in that it was likely not in Euclid's original manuscript. Euclid's originals have long since been lost, and all we have are copies of copies of copies. People would often write notes in the margins of books, and sometimes copyists would copy those notes into the main text of their copy. It is thought something like that must have happened here because we do have some papyrus fragments of very old copies of Euclid, and this proposition seems not to have been in those copies. The proof also contains some inaccuracies that are not typical of Euclid. Since I.39 is a special case of I.40, we'll just prove I.40 below, being careful to avoid the inaccuracies of “Euclid's” proof.
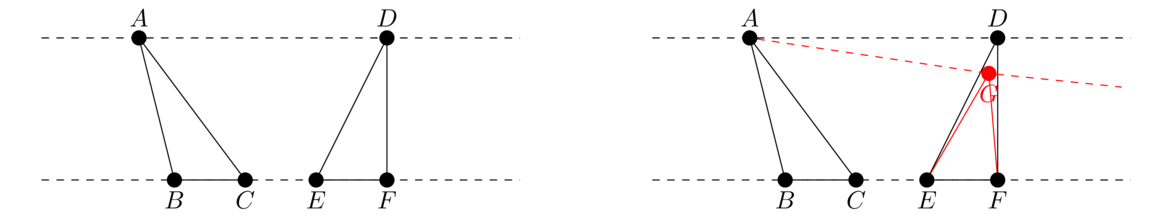
Recall that Proposition I.34 says that the diameter of a parallelogram breaks it into two triangles, each half the area of the parallelogram. This proposition says that for any triangle and parallelogram on the same base with the same height, the triangle's area will be half the parallelogram's.

You may have noticed that Euclid doesn't use a lot of numbers. He doesn't measure lengths, angles, or areas, except relative to other things. For instance, the previous proposition says a particular triangle's area is half the area of a particular parallelogram. But he doesn't ever say a certain figure has area 48, for instance. We, as modern mathematicians, usually measure area with a square unit, like square inches or square centimeters. A square inch is the area of a square with side length 1. So if we say something has area 48 in2, we are saying it contains an equivalent area to 48 one-inch squares.
A rectangle with length ℓ and width w can hold ℓ of these squares lengthwise and w of the widthwise, for a total of ℓ w squares. So we say its area is A = ℓ w. We can then use this along with Proposition I.35 to get a formula for the area of a parallelogram with base b and height h. The key idea is that a rectangle is a special case of a parallelogram, so if we place the a rectangle with dimensions b and h on the same base and in the same parallels as the given parallelogram, then they must have the same area. Thus, the area formula for parallelograms is A = bh. Then, using Proposition I.41, the area formula for a triangle must be A = 12 bh.
One other formula that's nice to know is the area of a trapezoid. If the two bases of the trapezoid are a and b, and its height is h, then the area is a+b2 h. Think of a+b2 as the average base size of the trapezoid.
Propositions I.42 to I.45
This section of propositions concerns quadrature, which is an older term for area. In this context, it is about finding a square with the same area as a given shape. This does take some work to get to. Euclid's goal in these next few propositions is to construct a parallelogram with the same area as a given polygon. In Book II, he finishes what he started here by extending it from parallelograms to squares.
This is related to “squaring the circle,” a phrase which has entered the English lexicon to mean something impossible. The ancients were interested using a straightedge and compass to construct a square with the same area as a given circle. No one was able to solve it, and eventually people figured it must be impossible. It was finally proved impossible in 1882, though some people still keep trying. It is possible to construct such a square with other tools, but if we are restricted to the two basic tools of a straightedge and compass, then it's impossible.

This proposition, as well as the next two, are lemmas leading up to Proposition I.45, which is an important theorem. The goal of this proposition, as shown above, is to construct a parallelogram with the same area as a given triangle. Further, we can specify what angle we want the parallelogram to have. If we choose it to be a right angle, we can make the parallelogram be a rectangle.

Then FECG is a parallelogram, and it shares base EC with △AEC. Therefore, by Proposition I.41, its area is twice the area of △AEC. Notice that △AEC has the same area as △ABE by Proposition I.38 since the two triangles have equal bases and are in the same parallels. So the area of △ABC is twice the area of △AEC, just like FECG. Thus △AEC and FECG have the same area.
This proposition mentions something called the “complement” of a parallelogram. This is not a common term. The figures below shows what it's about. The two shaded parallelograms in each figure are the complements. To get them, we start by drawing a diameter and choosing any point on it. We then draw lines through that point parallel to each of the sides. This creates two parallelograms on opposite sides of the diameter, which are the complements. This proposition claims that they always have equal areas.

Let ABCD be the parallelogram and draw the diameter AC. Choose a point K on the diagonal and draw HG parallel to AB and EF parallel to AD. We need to show that HKFD and EBGK have the same area.

Note that AEKH, KGCF, and ABCD are parallelograms. So by I.34, △AEK and △AKH have equal areas, as do △KGC and △KCF, as well as △ABC and △ACD from the big parallelogram. From △ABC, subtract off triangles AEK and KGC, and we are left with one of the complements EBGK. From △ACD, subtract off triangles AHK and KFC to get the other complement HKFD. In both cases, the big triangles and the pieces being subtracted match exactly in area, meaning the two complements must have the same area.


Though it's phrased a little differently, this proposition is just like Proposition I.42, but it's a stronger statement in that not only can we specify the angle, but we can also specify exactly what one of the sides should be, as shown above. Having this flexibility will be useful in proving Proposition I.45.
Let the given line be AB. Use Proposition I.42 to construct parallelogram BGFE with the same area as the given triangle and with the given angle being placed at B.

Next, use Proposition I.31 to make a line parallel to BG at A and extend line FG until it hits this line at a point H. Connect HB. Then extend HB and FE until they meet at a point K. In the picture below, it's clear they meet, but we should show why. We know that AH ∥ EF, so by Proposition I.29, ∠AHG+∠EFG = 180°. Since ∠BHG is contained in ∠AHG, we must have ∠BHG+∠EFG < 180°. Thus by Postulate 5, the lines HB and EF containing these angles must meet.

Now draw a line parallel to HF at K and extend lines HA and GB up to meet it at points L and M. Notice that the figure thus created looks similar to what we had in Proposition I.43. Using that proposition, we know that LABM and BGFE have equal areas, and remember that BGFE was constructed to have the same area as the given triangle. Also, by Proposition I.15, ∠MBA = ∠GBE. And LABM is on side AB, so LABM satisfies all the criteria of the desired parallelogram.

The preceding proof has a lot going on, but it can be summarized as follows: Use Proposition I.42 to construct a parallelogram with the right area and angle. Then extend out the figure to build a parallelogram on AB matching the setup of Proposition I.43.
By “rectilineal figure,” Euclid means a figure all of whose sides are straight lines. Nowadays, we use the term polygon for this. The proof Euclid gives is specifically for quadrilaterals, four-sided polygons. After giving the proof, we will see how to make it work for any polygon.

Assume we are given a quadrilateral. Start by breaking it into two triangles, T1 and T2, by connecting two opposite sides. Use I.42 to create a parallelogram FKHG with the same area as T1 and with an angle matching the given angle. Then use I.44 to create parallelogram GHML, sharing side GH with the first parallelogram, and having the same area as T2 and with an angle matching the given angle. We now have to verify that the two parallelograms meet up nicely to create one large parallelogram, FKML. This verification will take some work.

To do this, we first have to show that KH and HM as well as FG and GL meet up to form straight lines. The tool for this is the converse of Proposition I.13, which is Proposition I.14. It says that if the sum of the angles where the lines meet is 180°, then they form a straight line. We will first show that KH and HM form a straight line. Since KF ∥ HG, we have ∠FKH+∠GHK = 180° by Proposition I.29. Since ∠FKH and ∠GHM were constructed to both equal the given angle, they are equal. Thus we have ∠GHM + ∠GHK = 180°, meaning KH and HM form a straight line by Proposition I.14.
Next, we show that FG and GL form a straight line. By the above, we know that KM is a straight line. And since KH ∥ FG, we must have KM ∥ FG. By Proposition I.29, the alternate interior angles ∠FGH and ∠GHM are equal. Adding ∠HGL to each gives ∠FGH+∠HGL = ∠GHM+∠HGL. And since HM ∥ GL, we have ∠GHM+∠HGL = 180° by Proposition I.29. Thus ∠FGH+∠HGL = 180°, so by Proposition I.14, FG and GL form a straight line.
Now that we know FL and KM are straight lines, we need to show that they are parallel to each other, as are FK and LM. For the latter, note that FK ∥ GH since they are part of the first parallelogram constructed, and GH ∥ LM since they are part of the second parallelogram constructed. Thus by Proposition I.30, FK ∥ LM. Also, since FKHG and GHML are parallelograms, we can use I.34 to conclude that FK = GH and GH = LM. This tells us that FK = LM. So we know two sides of FKML are equal and parallel. Thus by Proposition I.33, the other two sides FL and KM are equal and parallel, making FKML a parallelogram.
As mentioned, this only handles the case of quadrilaterals, not polygons in general. But we can extend it as far as we like. For instance, given a pentagon, we can carve a triangle off of it by connecting any two vertices that are two steps away from each other. This produces a triangle and a quadrilateral. We can apply the above result to produce a parallelogram in the given angle with the same area as the quadrilateral and then use Proposition I.44 to attach a parallelogram to the end of the first parallelogram, just like in the proof above. And the same proof as above would work to show that the two parallelograms fit together to form one large parallelogram.

So now we can do pentagons. For hexagons, play the same trick. Carve off a triangle, apply the pentagon fact to create one parallelogram, and then attach the another equalling the triangle's area using Proposition I.44. The proof that everything fits together is again the same as earlier. And we can keep doing this indefinitely. The way to make all of this formal is to use a proof by induction. For the induction step, we would assume that we can construct the desired parallelogram for polygons with n sides and we would use the construction described above to construct the desired parallelogram for any polygon with n+1 sides. Euclid's proof is essentially the same as the induction step, just done in the case of going from n = 3 to n = 4. Mathematical induction wasn't a proof technique available to Euclid, but we can use it.
Propositions I.46 to I.48
Book I concludes with a few interesting propositions, including a very famous one (Proposition I.47). Recall that Euclid's very first proposition is the construction of an equilateral triangle. Proposition I.46 is about constructing an equilateral quadrilateral, i.e. a square.
Let the line AB be given. Use Proposition I.11 to construct a line perpendicular to AB at A and use Proposition I.3 to mark off a point D on that line such that AD = AB. Then use Proposition I.31 to construct a line parallel to AB through D and a line parallel to AD through B. Let E be the place these lines meet.
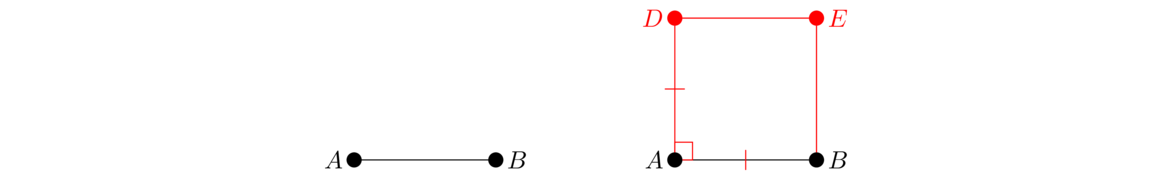
This is our square, DABE, and we need to show that it really is a square. That is, we need to show that all four sides are equal and all four interior angles are right. Note that AB ∥ DE and AD ∥ BE so that DABE is a parallelogram. Thus by Proposition I.34, DE = AB and AD = BE. Since AB = AD, all four sides are equal. Proposition I.34 also tells us that ∠E = ∠A and ∠B = ∠D. We know already that ∠A is right, so if we can show that ∠D is right, we will be done. Using Proposition I.29, we have that ∠A + ∠D = 180° since AB ∥ DE. Thus ∠B = 90° because ∠A = 90°.
This proposition shows how to construct a square using just a straightedge and compass. But where are all the uses of the straightedge and compass? They are hidden in our uses of Propositions I.3, I.11, and I.31. We could go back to the proofs of those, which in some cases rely on earlier propositions, and eventually trace back until we eventually get to the point where 6 circles and 3 lines are drawn. See the bottom of the page at https://mathcs.clarku.edu/~djoyce/java/elements/bookI/propI46.html for what this looks like. Euclid's construction is only one of many possible ways to construct a square. There are ways that use less total circles.
This is the very famous Pythagorean theorem. We would usually phrase the conclusion as a2+b2 = c2. Euclid, however, didn't have the notation we have for squares. He likely didn't even think of things in terms of equations like this. His statement is purely geometrical. When he talks about a square on a side, he literally means the geometrical square constructed from that side. On the left below is how we usually think of the Pythagorean theorem. On the right is how Euclid thought of it, purely in terms of areas of squares.
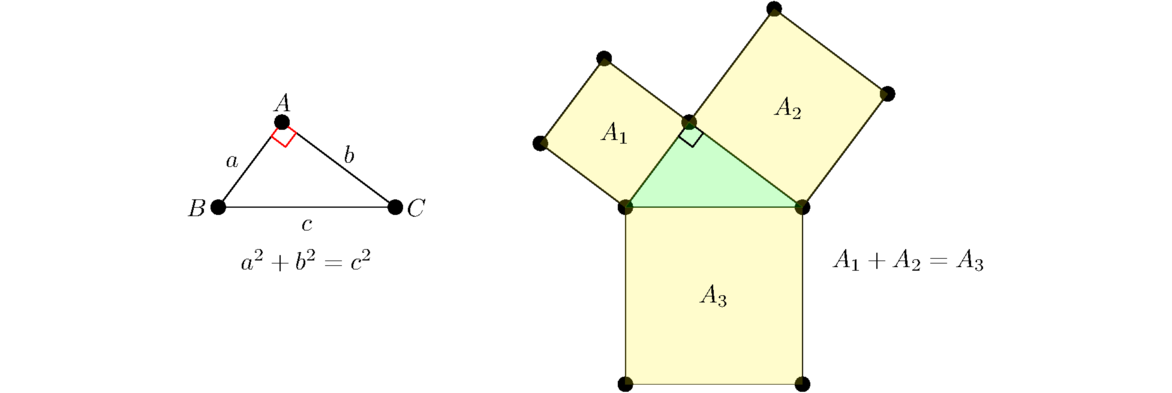
We will present Euclid's proof here. It's a bit involved. After that we will look at a few simpler proofs.
We first have to show that the squares and the triangle meet up nicely, namely that AC and AG are in a straight line, as are AB and AH. By Proposition I.14, to show AC and AG are in a straight line, we need to show that ∠GAB+∠BAC = 180°. This is true because both angles are right, one an interior angle of a square, and the other being the right angle of the triangle. Lines AB and AH are in a straight line for a similar reason.
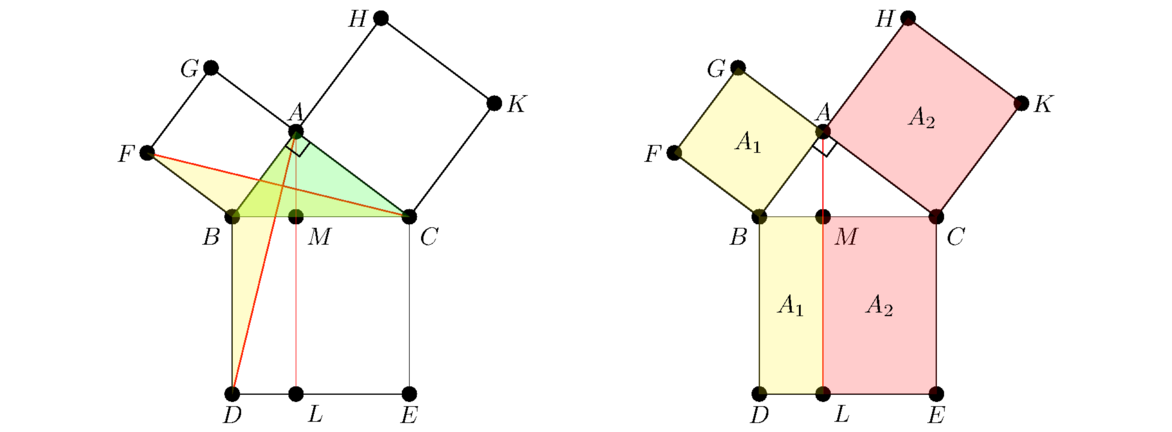
We next show that △ABD≅ △FBC using SAS. To do this, note that AB = FB because they are sides of the same square, and BC = BD for the same reason. We also have ∠ABD = ∠FBC because each of those angles consists of ∠ABC along with a 90° interior angle of a square.
Using Proposition I.41, the area of △ABD is half the area of BMDL. This is because they are on the same base, BD, and in the same parallels BD and AL. Similarly, using Proposition I.41, the area of △FBC is half the area of ABFG. They are on the same base FB and in the same parallels FB and GC. Since △ABD≅ △FBC, they have the same area, so BMDL and ABFG have the same area as well.
A very similar argument shows that the right square, ACKH, has the same area as MCEL. And that finishes the proof, since square BCED is composed of BMDL and MCEL, whose areas are equal to the areas of ABFG and ACKH, respectively.
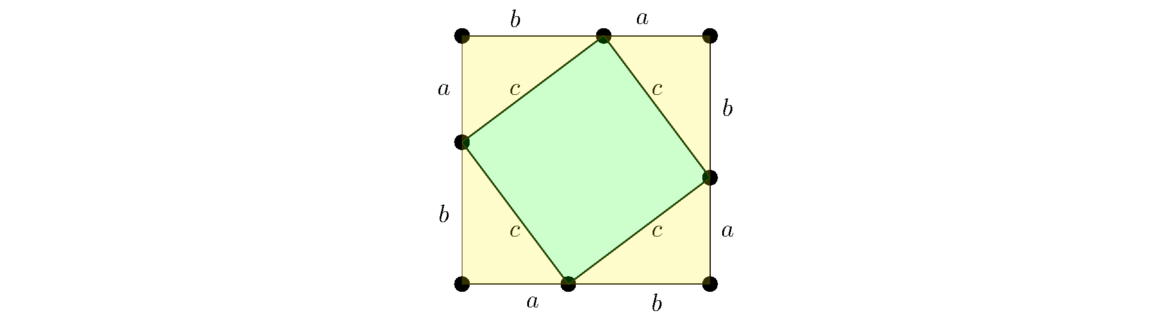
There are several hundred known proofs of the Pythagorean theorem. One was even developed by a former president of the United States, James Garfield, after a conversation he had with some other members of Congress when he was serving there. Here is probably the simplest proof I know of. In the figure below, the larger outside square has side length a+b and area (a+b)2. That square is composed of the inner tilted square with side length c and four congruent right triangles with legs equal to a and b. Adding up the areas of the inside components gives c2+4(12 ab), which simplifies to c2+2ab. This must equal the area of the whole figure, thinking of it as a square with side length a+b, so we get (a+b)2 = c2+2ab. Expand the left side to get a2+2ab+b2 = c2+2ab and simplify to get a2+b2 = c2.
Here is another proof that uses this same figure. This one doesn't require any algebra. In the figure below on the left, there are four congruent triangles with legs a and b and hypotenuse c. Imagine moving the bottom right triangle to fit right next to the top left triangle as part of the inside square. And also move the upper right triangle to fit right next to the lower left triangle in a similar way. As we move them, change the shading so that the places they vacate get shaded the same color as the inner square. We end up with the picture below on the right.
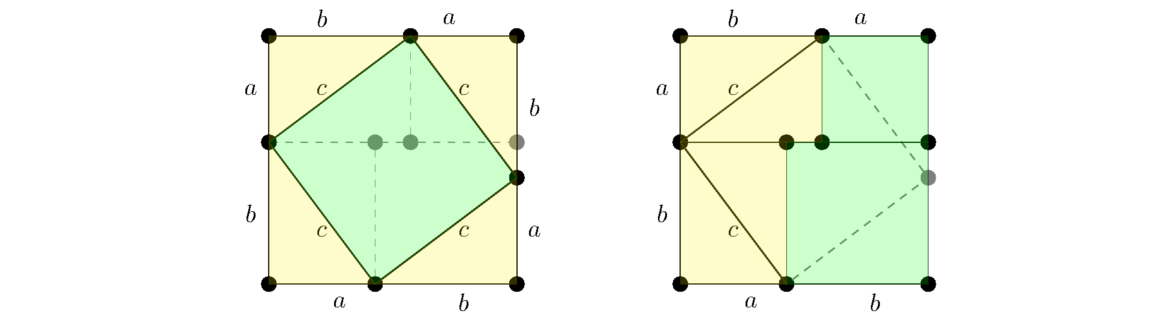
The total areas of the darker and lighter shaded areas stays the same between both figures since as we move the two triangles, the area of the middle square that they replace is equal to the area from where they came, which is shaded to the darker color. In the left figure, the darker color corresponds an area of c2 and in the right figure, the darker color corresponds to an area of a2+b2. Thus a2+b2 = c2.
We're all familiar with the famous 3-4-5 triangle, whose sides satisfy 32+42 = 52 and are all whole numbers. There are other such triangles, like 5-12-13 and 7-24-25. A tuple of three whole numbers (a, b, c) that satisfies a2+b2 = c2 is called a Pythagorean triple. Pythagorean triples have been of interest for a very long time. The 3-4-5 triangle has been used by carpenters for thousands of years to lay out things on at right angles. A Babylonian cuneiform tablet from around 1800 BC called Plimpton 322 seems to show several Pythagorean triples.
Given a Pythagorean triple (a, b, c), any multiple of it, (na, nb, nc), is also a Pythagorean triple. For instance, building off of (3, 4, 5), we get (6, 8, 10), (9, 12, 15), (12, 16, 20), etc. So there are infinitely many Pythagorean triples. But are there infinitely many that are not multiples of any others? Pythagorean triples that are not multiples of others are called primitive. For instance, (3, 4, 5), (5, 12, 13), and (7, 24, 25) are all primitive Pythagorean triples.
Euclid himself found a way to generate new primitive Pythagorean triples in Proposition X.29. We won't cover the details here, but if we translate it into modern notation, it gives the formula (m2–n2, 2mn, m2+n2) to generate Pythagorean triples. The triples will be primitive if m and n share no common factors other than 1 and at least one of them is even. We also want m > n to keep the numbers positive. Here are a few the formula generates:
| m | n | triple |
| 2 | 1 | (3, 4, 5) |
| 3 | 2 | (5, 12, 13) |
| 4 | 1 | (8, 15, 17) |
| 5 | 2 | (20, 21, 29) |
| 5 | 4 | (9, 40, 41) |
| 7 | 2 | (28, 45, 53) |
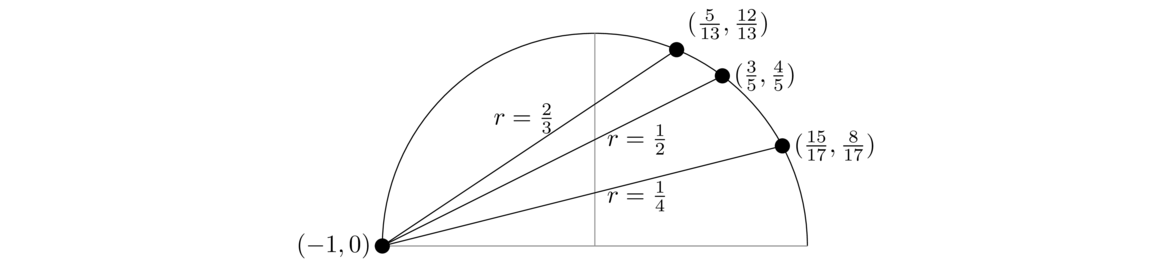
Pythagorean triples are also related to rational points on the unit circle. These are points (x, y) where both x and y are rational numbers. It's possible to generate all of them by starting at the point (–1, 0) on the unit circle and seeing where lines with rational slopes hit the circle. See below for a few examples. A little algebra with the equations of the line and unit circle finds the coordinates of those points and shows their relationship to Pythagorean triples.
Rational points on other curves, in particular what are called elliptic curves, are an important focus of modern mathematics, with applications to cryptography.
This proposition is the converse of the Pythagorean theorem. In particular, it says that if sides a, b, and c of a triangle satisfy a2+b2 = c2, then the triangle must be right.
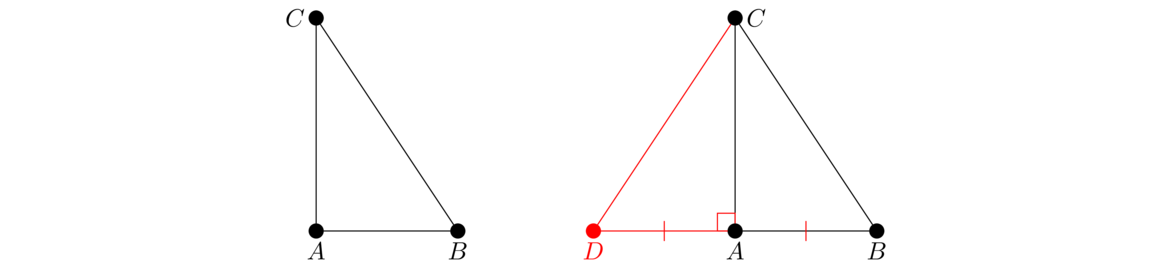
Join DC to create △ADC. Since △ADC is right, by Proposition I.47, AD2+AC2 = DC2. The hypothesis of the proposition is that AB2+AC2 = BC2, and since AB = AD, we must have AD2+AC2 = BC2. Thus DC2 = BC2. Since DC and BC can't be negative, we have DC = BC. Since BC = DC, AB = AD, and AC is common, we have △ABC ≅ △ADC by SSS. Therefore, ∠CAB = ∠CAD, and since ∠CAD is right, ∠CAB must be right as well.
Book II
Introduction
Much of Book II is about what is sometimes called geometric algebra. Algebra wasn't invented until long after Euclid, but Euclid still solved many problems that would now be solved with algebra. But he solved them with geometry. For instance, Proposition II.11 is a purely geometric approach to solving the equation x2 = a(a–x) for x. Book II starts off with two definitions.
- Any rectangular parallelogram is said to be contained by the two straight lines containing the right angle.
In Book II, Euclid will often describe a rectangle by giving just two of its sides and calling it the rectangle contained by those two sides. For instance, in the figure below on the left, we could describe that rectangle as being contained by AB and AC. Once we have those two line segments, the rest of the rectangle is completely determined. We could also describe the rectangle using other sides, like being contained by AC and CD or by CD and BD. Euclid sometimes describes rectangles by just giving two corners. For instance, the rectangle below on the left could be called AD or BC.
- And in any parallelogrammic area let any one whatever of the parallelograms about its diameter with the two complements be called a gnomon.
A gnomon is an L-shaped figure, like below on the right. The “complements” in the definition are the parallelograms first described in Proposition I.43. If you're just reading these notes, the term is not too important, but if you're reading Euclid's original proofs, you'll need to know that term.

Propositions II.1 to II.6
Some of the proofs in this section can get a little tedious, so we will mostly just sketch the proofs. In most cases, we will show how the geometry relates to statements in modern algebraic notation. We will do things a little out of order and start with the second proposition.
It takes a little work to understand exactly what he's trying to say, We're given a line AB, and we pick a random point C on it. We then look at the following three things:
- A rectangle with length equal to AC and width equal to AB.
- A rectangle with length equal to CB and width equal to AB.
- A square with side length equal to AB.

If we label AB as x and CB as y, then sides AB and AD have length x+y. Using the area formula for rectangles gives x(x+y) + y(x+y) = (x+y)(x+y). So we see that Proposition II is a special case of the distributive rule from algebra.
Again, it takes some work to understand exactly what he's getting at. Often, it's easier to look at the picture he provides along with the first sentence or two of his proof. The picture is below. Here is how he starts the proof: “For let the straight line AB be cut at random at C; I say that the rectangle contained by AB, BC is equal to the rectangle contained by AC, CB together with the square on BC.” In the picture below on the left, the height is chosen to be the same as BC.

The proof of this is very similar to the proof of Proposition II.1, so we will skip it. Algebraically, if we let x be the length of AC and y be the length of CB, then BE has length y and area formulas give us that xy+y2 = (x+y)y, another algebraic fact that is true by the distributive law.
Proposition II.1 is actually more general than II.2 and II.3. People think that maybe II.2 and II.3 were original to Euclid and II.1 was added later as a natural generalization. Here is the statement:
This is essentially a general distributive law. Translated into algebra, it says that a(x1+x2+… xn) = ax1+ax2+…+axn. In this, x1, x2, etc. are the lengths of the segments created by breaking up the one line, and a is represents the length of the other line. This is shown geometrically in the case of five segments below on the left. The area of the rectangle as a whole is a(x1+x2+x3+x4+x5), and the area of the rectangle taken as a sum of its pieces is ax1+ax2+ax3+ax4+ax5.

Euclid (or whoever) proves it only in the special case of three segments. His proof starts by assuming lines A and BC are given. He then constructs the figure shown above on the right. He marks off the points D and E where line BC is randomly cut. Then he draws a line perpendicular to BC and marks a point G on it so that BG equals A. Then he draws lines DK, EL, and CH parallel to BG. Having constructed the figure, he uses Proposition I.34 to verify that all the subrectangles have the desired dimensions and he notes that the subrectangles comprise the big rectangle.
To see this proposition algebraically, imagine breaking the straight line into pieces of length x and y. The “whole” has length x+y. The “squares on the segments” are two squares, one having side length x and the other having side length y. The “rectangle contained” by the segments has dimensions x by y. Putting this all together with area formulas, it says (x+y)2 = x2+y2+2xy, a fact we are very familiar with from algebra. The figure below on the left shows how this all works.
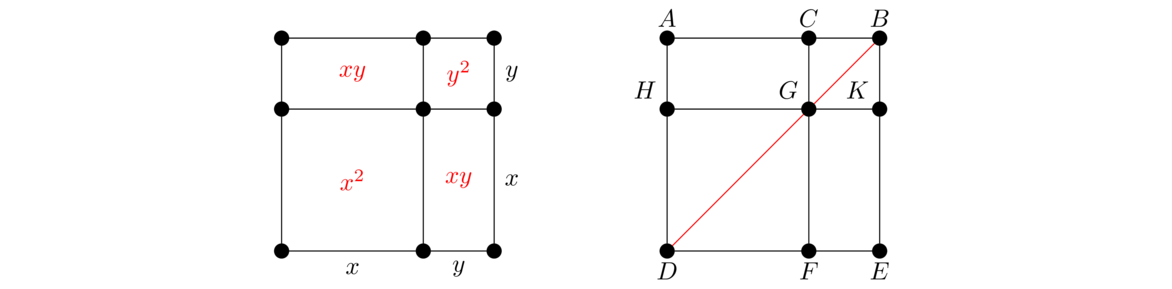
The picture on the left above is good to show students who are first learning how to expand (x+y)2 to convince them of where the 2xy term comes from. That picture is enough to convince modern eyes that the result is true, but Euclid's proof is quite a bit more involved. We will outline it here.
He lets AB be the given line and chooses a random point C on it. Then he constructs the square on AB using Proposition I.46, and he connects DB. From there, he draws CF parallel to AD, letting G be the point where it meets DB. Then he draws HK parallel to AB through G. This creates the figure above on the right.
He now verifies that CGKB really is a square. To do this he first notes that ∠ADG = ∠CGB by Proposition I.29 (since CF ∥ AD), and that ∠ADG = ∠CBG by Proposition I.5 (since AB = AD). So ∠CGB = ∠CBG, meaning CB = CG by Proposition I.6. Then by I.34, the other two sides of CGKB must also equal these, so CGKB is equilateral. To be a square, it also has to have all right angles. We know that ∠CBK is right because it is part of the outside square, and since CB ∥ GK, we must have that ∠CBK+∠BKG = 180°. Combining these, we get that ∠BKG is right. Then apply I.34 to get that the other two angles in CGKB are right. A similar proof shows that HDFG is also a square. From there, he applies Proposition I.43 to show that the complements AHGC and GFEK have equal areas. Finally, he quickly verifies that the four internal pieces all have the dimensions desired in the proposition's statement, and the proof is done.
As Book II progresses, the statements get trickier to parse. Here are the first sentence of the proof: “For let a straight line AB be cut into equal segments at C and into unequal segments at D; I say that the rectangle contained by AD, DB together with the square on CD is equal to the square on CB.” We can interpret this as a statement about areas. Shown below shaded are the two areas he is saying are equal.
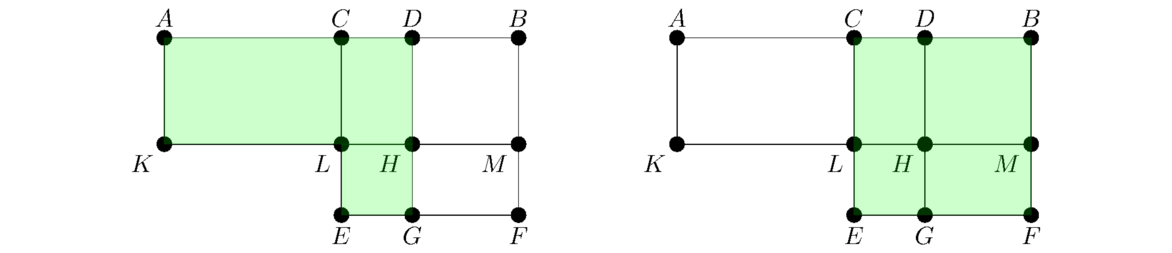
In this figure, C is the midpoint of AB and D is some other point on that line. The length of BM is the same as the length of DB, and the length of BF is the same as the length of CB. In particular, DHMB and CEFB are squares.
Here is why the proposition is true. We know from Proposition I.43 that CLHD has the same area as HGFM. Therefore, the area shaded in the figure above on the left is the same as the area shaded in the figure below on the left. But then, since AC = CB, we know that AKLC has the same area as CLMB, so the figure below on the left has the same area as the figure above on the right.
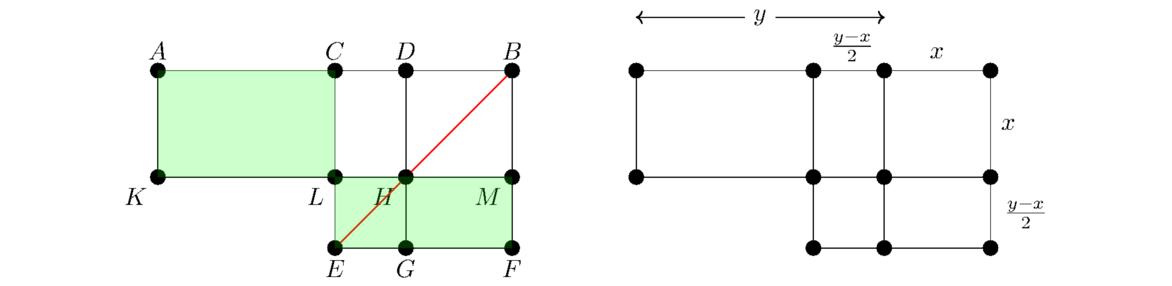
This proposition does have an interesting algebraic interpretation. Let AD be y and let DB be x. Then, using the fact that C is the midpoint of AB gives 2(x+CD) = x+y, which simplifies into CD = y–x2. We then get that that rectangle AKHD has area xy, square LEGH has area (y–x2)2, and square CEFB has area (x+y–x2)2, which is (y+x2)2. Putting this together with the conclusion of the proposition gives the following:
 This is an occasionally useful algebraic fact. It allows us to rewrite a product as a difference of two squares. One use is for mental math. Suppose we want to compute 23 × 17 in our heads. Take x = 23 and y = 17 in the identity above. Then (x+y)/2 = 20 and (x–y)/2 = 3, so 23 × 17 = 202–32. Both 202 and 32 are easy to do mentally, and we do 400–9, which equals 391. You can use this whenever the numbers being multiplied are relatively close together and centered around something whose square you can compute easily (in this case 20).
This is an occasionally useful algebraic fact. It allows us to rewrite a product as a difference of two squares. One use is for mental math. Suppose we want to compute 23 × 17 in our heads. Take x = 23 and y = 17 in the identity above. Then (x+y)/2 = 20 and (x–y)/2 = 3, so 23 × 17 = 202–32. Both 202 and 32 are easy to do mentally, and we do 400–9, which equals 391. You can use this whenever the numbers being multiplied are relatively close together and centered around something whose square you can compute easily (in this case 20).
This is very similar to the proposition above. The difference is that D doesn't lie between A and B. Here is how Euclid starts the proof: “ For let a straight line AB be bisected at the point C, and let a straight line BD be added to it in a straight line;
I say that the rectangle contained by AD, DB together with the square on CB is equal to the square on CD.” In particular, this is saying that the area shaded below on the left equals the area shaded below on the right. Note that C is the midpoint of AB, DM is equal to BD, and DF is equal to CD.
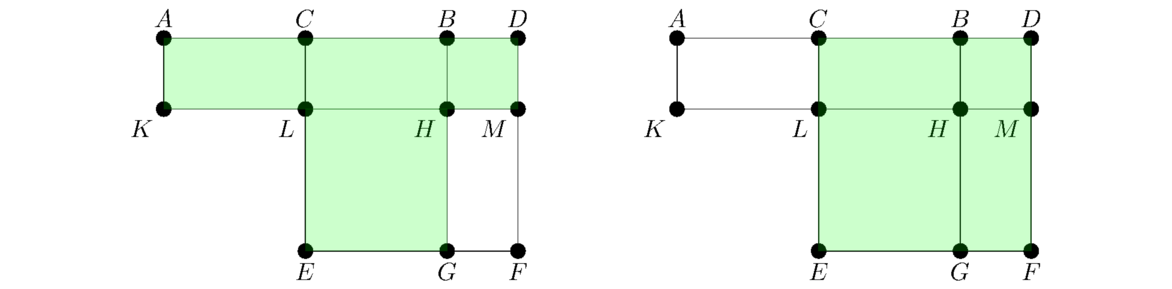
To see why the proposition is true, the key is to show that the unshaded areas are the same in both figures. The unshaded area in the left figure, rectangle HGFM, is equal in area to rectangle CLHB by Proposition I.43, since they are complements. And rectangle CLHB is equal in area to rectangle AKLC because C is the midpoint of A and B. Since rectangle AKLC is the unshaded area in the right figure, we are done.
We will skip Propositions II.7 to II.10, which are all of a similar character to the preceding few propositions.
Propositions II.11 to II.14
This is illustrated below. We are given a line segment of length a, and we break it at a certain point, x units from the left edge. We want x to be chosen so that the area “contained by the whole and one of the segments” (the rectangle with dimensions a by a–x) has the same area as “the square on the remaining segment” (the square with side x). In equation form, this is asking us to solve a(a–x) = x2.
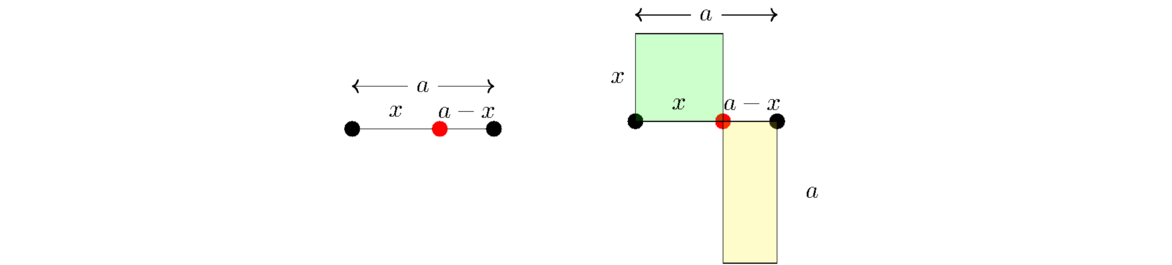
Shown below are three possible places to break up the given line segment. We can see that if we break it too far to the left, then the square has smaller area then the rectangle, and if we break it too far to the right, then the square has larger area. But there must be some point in the middle where the areas exactly balance out.


Using Postulate 2 and Proposition I.3, extend AC to a point F such that EF = EB. Then use Proposition I.46 to create square FAHG on FA. Finally, extend GH until it meets CD at a point K. The point H is the answer to where we should cut AB.

We now need to show why H works as the cut point. We'll use a modern approach that is mostly equivalent to what Euclid does, though he uses Proposition II.6 where we'll use some algebra. Let a be the length of AB, let x be the length of AH, and let h be the length of EB. Then AC has length a since it is part of a square with AB, and AE has length a/2 since E is the midpoint of AC. Also, since EF = EB, the length of EF is h, and since FAHG is a square, the length of AF is x. See the figure below.
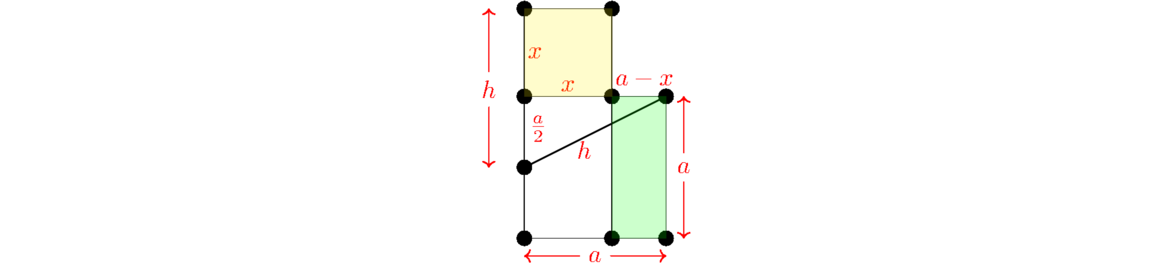
To show that H is the point we want, we need to show that a(a–x) = x2. To do this, start with the Pythagorean theorem on △ABE. It gives a2+(a/2)2 = h2. We also have h = x+a/2 from segment EF. Plug this into the first equation to get a2+(a/2)2 = (x+a/2)2. Expand both sides to get a2+a2/4 = x2+ax+a2/4. This simplifies into a2 = x2+ax. Subtract ax and factor to get a(a–x) = x2, as desired.
This proposition is about solving a(a–x) = x2. We can do this easily using the quadratic formula, but Euclid did not have the quadratic formula. Instead, he finds the solution by using a straightedge and compass. It's nice to know that problems are solvable in this way and not just with algebra. Proposition II.11 turns out to be useful in Book IV when Euclid constructs a regular pentagon.

Since ∠D is right, the Pythagorean theorem applies. On △BDA, it gives d2+e2 = b2, and on △BDC, it gives (d+a)2+e2 = c2. Solve the first equation for e2 and plug into the second to get (d+a)2+(b2–d2) = c2. Expand the left side to get d2+2da+a2+b2–d2 = c2, and simplify to get a2+b2+2ad = c2.
This proposition is an extension of the Pythagorean theorem to obtuse triangles. It is saying in the figure above that a2+b2+2ad = c2. Our proof relies on some algebra. Euclid's proof is similar, but it relies on Proposition II.4, which we saw earlier is equivalent to (x+y)2 = x2+2xy+y2, which we use in our simplifications above. The next proposition is like the previous one, but it's for acute triangles. It says that a2+b2–2ad = c2.

We have ∠ADB = ∠ADC = 90°, so we can use the Pythagorean theorem. Using it on △ADB gives d2+e2 = b2, and using it on △ADC gives (a–d)2+e2 = c2. Solving the first equation for e2 and plugging into the second gives (a–d)2+(b2–d2) = c2. Expand out the left side to get a2–2ad+d2+(b2–d2) = c2. This simplifies into a2+b2–2ad = c2.
It might not be obvious in the proofs above where we use the fact that the triangle is obtuse or acute. In both cases, we are drawing a perpendicular line from the apex of the triangle to the base, hitting at point D. In a right triangle, this point would exactly coincide with one of the other vertices. In an obtuse triangle, D ends up outside the triangle, and in an acute triangle, D ends up inside. In the latter two cases, we are making a right triangle out of our given triangle when we place the point D, and these theorems tell us how far off c2 is from equalling a2+b2. In the obtuse case, c2 is 2ad more than a2+b2, and in the acute case it is 2ad less.
Propositions II.12 and II.13 are Euclid's equivalent of the law of cosines. Below is the figure from Proposition II.12 with ∠BAC = θ. We have ∠BAD = 180°–θ, and then cos(180°–θ) = b/d. Note that cos(180°–θ) = – cos(θ), and we can solve for d to get d = b cos(θ). Plugging this in, we get a2+b2–2ab cos(θ) = c2.
This is the law of cosines. It's not hard to show that it also works for acute triangles. And it works for right triangles too, since cos(90°) = 0. The main use for the law of cosines is if we have any two sides and an angle in a triangle, then we can work out what the third side must be.

Proposition I.45 was about constructing a parallelogram with the same area as a given polygon (rectilineal figure). Proposition II.14 takes that further by producing a square with the same area as the polygon. Constructing a square with the same area as a given figure is almost the same as giving a formula for its area, considering that modern area formulas are given in square units. The proof we will give below uses a little bit of algebra. But Euclid didn't have algebra. His proof relies on Proposition II.5, which is why this proposition is placed in Book II instead of Book I. Euclid's proof is similar to the one given below, though it relies on Proposition II.5 in place of the algebra we do.
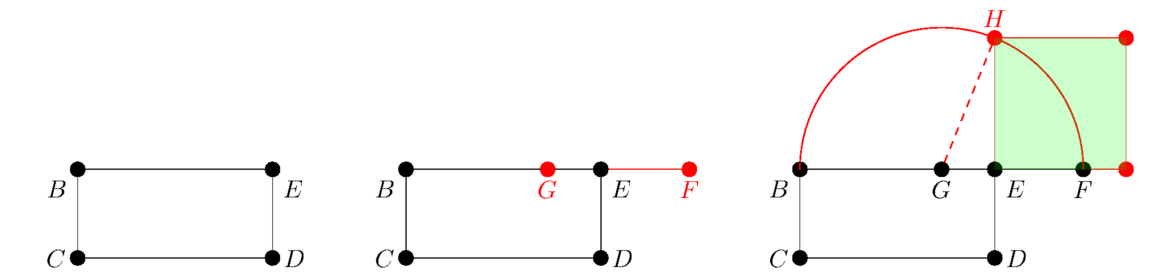
So now we need to show that the square constructed on HE has the same area as rectangle BCDE. To do this, label the sides as below. Namely, let the radius of the circle be c, meaning that GB and GH are both length c. Let the length of GE be a, meaning that both BE and CD have length c+a. Let d be the length of EF, which is the same as ED. Let b be the length of EH. Showing that the square on HE has the same area as BCDE is equivalent to showing that b2 = d(c+a).
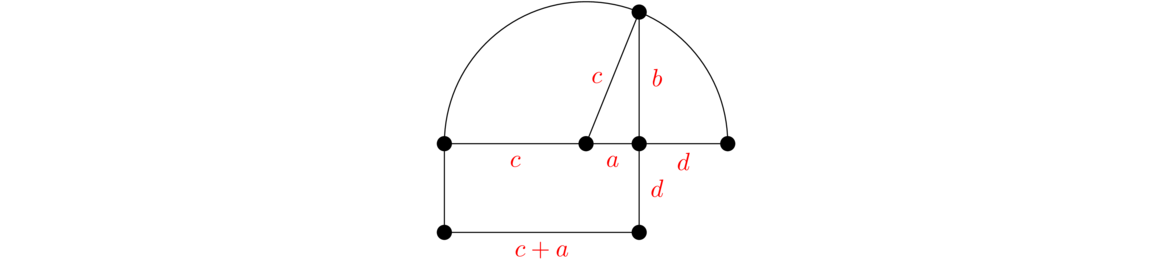
To show b2 = d(c+a), start with the Pythagorean theorem on △GEH, which gives a2+b2 = c2. So b2 = c2–a2. Then, since GF is a radius of the circle and GF equals a+d, we have c = a+d. Plug this into the previous equation to get b2 = (a+d)2–a2. This simplifies into b2 = a2+2ad+d2–a2 or b2 = 2ad+d2. Factor out d to get b2 = d(2a+d). Finally, since c = a+d, we have d = c–a, and plugging this in gives b2 = d(2a+c–a) or b2 = d(c+a), as desired.
Book III
Book III is all about circles. We cover some of the propositions, but not all of them. First, here are a few terms to know:
- A chord is a line segment with both endpoints on a circle. Euclid doesn't use the term, but it's still a convenient term to have.
- A chord that passes through the center is called a diameter.
- Euclid used the term circumference to refer to a part of the circle itself. Modern mathematicians use the term arc for this.
Also, if you're reading Euclid's original proofs, he will often describe a circle by giving three points on the circumference. Modern mathematicians usually specify circles by giving their center and radius, but Euclid will often instead give three points, and it is true that a circle is uniquely determined by three points on its circumference (which we won't prove here).
Propositions III.1 to III.3
Recall that Postulate 3 says that we can draw a circle with a given center and radius. So why would we need this proposition? The idea is that if someone hands us an already drawn circle, we can use this proposition to locate the circle's center.
To see why it's the center, try a proof by contradiction. Suppose some other point G were the center. Join G to A, B, and D, and look at △GDA and △GDB. We know that GA = GB since both are radii of the circle, AD = BD since D was defined as the midpoint of AB, and side FD is common. So by SSS, the triangles are congruent. This means ∠GDA = ∠GDB. By the definition of right angles, this means that both of these angles are right. But that's a problem because ∠CDB and ∠CDA were defined to be right, and ∠GDB is contained in one of those (∠GDB if G is drawn like above). So we have a contradiction. So G must lie on line CE, and the center must be the midpoint of this line, which is F.
Euclid gives the following corollary to this proposition:
From this it is manifest that, if in a circle a straight line cut a straight line into two equal parts and at right angles, the centre of the circle is on the cutting straight line.
This follows from the contradiction part of the proof. If the center were not on the cutting line, then we could use SSS and get a contradiction in the same way as in the proof.

This is one of those statements that seems pretty obvious, but it does take a little work to prove it. The proof given above is similar to Euclid's original, but a little different in that Euclid's proof is by contradiction. This result is the key part of proving that any disc (a circle along with its interior) is convex. In particular, any line drawn from one point of the disc to another point in the disc must lie completely within the disc.
Put into slightly more modern terms, this says a diameter bisects a chord that's not a diameter if and only if it is perpendicular to that chord.
Let the circle be given, let E be its center, let CD be a diameter, let AB be a chord, and let F be where the chord and diameter meet. Join EA and EB.
This is an if and only if proof. First, we'll assume that the chord is bisected and prove that ∠EFA = ∠EFB = 90°. So we're assuming that AF = BF. We also know that EA = EB since both are radii. Therefore, since EF is common to both △EAF and △EBF, those triangles agree in all three sides and thus are congruent by SSS. This means that ∠EFA = ∠EFB. By the definition of right angles, these angles must both be right.
Next, we will assume ∠EFA and ∠EFB are both right and use that to prove that AF = BF. Since EA = EB, △EAB is isosceles, and by Proposition I.5, ∠EAF = ∠EBF. So △EAF and △EBF agree in two angles. They also agree in the shared side EF, so by AAS, they are congruent. This means that AF = BF.
Propositions III.16 to III.19
This group of propositions are all closely related. If you try drawing lines and circles, you'll see that one of three things can happen: the line misses the circle completely, the line just skims the edge of the circle at one point, or the line hits the circle in two points. In the third case, the line is called a secant line, and in the second case, the line is called a tangent line. Euclid doesn't use the term tangent. He instead says that the line “touches” the circle.

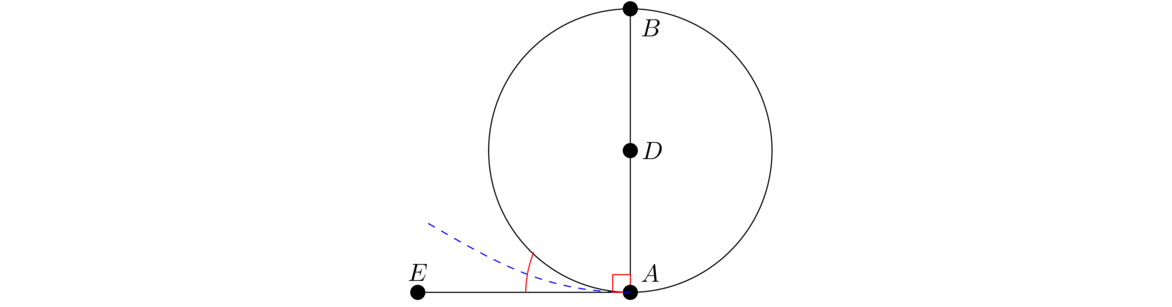
This proposition says three things:
- If we pick a point on a circle and draw a line at right angles to the diameter at that point, then the line will lie outside the circle.
- It's not possible to fit any other lines in between that line and the circle.
- The curvy angle formed between the line and circle has a measure smaller than any positive angle.
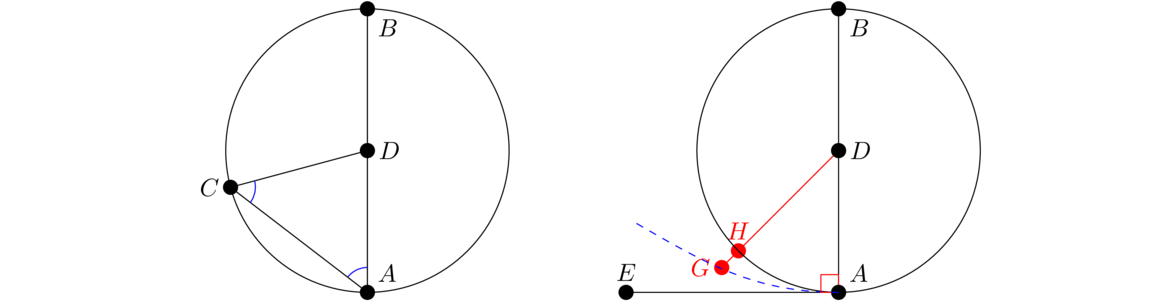
Next, we show that we can't fit another line in between the circle and the line we drew Again, by contradiction, suppose it were possible. This is illustrated in the figure above on the right, where we're attempting to fit the impossible dashed line in between the circle and line AE. Use Proposition I.12 to draw a line from the circle's center D, perpendicular to the impossible line, meeting it at G and meeting the circle at H. Then ∠DAG < 90° since by Proposition I.17 △DAG can't have two right angles. Then by Proposition I.19, DA > DG since DA lies opposite a right angle and DG lies opposite an acute angle. But we have DA = DH because both are radii, meaning we have DH > DG, which is impossible since we are trying to fit line AF (which G lies on) outside the circle (where H lies).
Finally, we show that the angle between the circle and the line is smaller than any positive angle. In order to create a nonzero angle in between the circle and line, we would need to be able to fit a line in there. But we just showed that we can't.

The last part of this proof is a little weird. It's the only occurrence in Euclid of a non-rectilineal angle, where both sides aren't straight lines. This is sometimes called a horn angle. The proof above shows that the measure of the horn angle between the circle and the line is infinitely small. But it looks like there really is some type of angle there, so it's not exactly 0 either. The angle represents a kind of infinitesimal, a positive quantity that is smaller than any positive number but yet not 0. Newton and Leibniz's original formulations of calculus relied heavily on infinitesimals. People criticized that approach. After all, how could you have something that is infinitely small and not 0? Yet the calculus created with infinitesimals worked and solved all sorts of real problems, like the motion of the planets. In the 1800s, calculus was reformulated in terms of limits, which didn't require any infinitely small nonzero numbers. In fact, modern math would define the curvy angle between the circle and line in terms of a limit of the angle between the line and tangents to the circle. Bringing things full circle, in the 1960s, something called non-standard analysis was developed which put infinitesimals on a solid mathematical and logical footing, developing a form of a calculus based on them.
Proposition III.16 has a corollary, stated below.
From this it is manifest that the straight line drawn at right angles to the diameter of a circle from its extremity touches the circle.
This is the most useful formulation of the proposition. In modern terms, if we pick a point on a circle and draw a line perpendicular to the diameter at that point, then the line will be tangent to the circle (i.e. meeting it at just one point). This is true because if it hit the circle in more than one point, then we would run into the same contradiction we got in the first part of the proof above.
Given a circle and a point, this proposition shows how to draw a line through that point that ends up tangent to the circle.

To see why this is the line we want, we will first show that △ABE≅ △FDE. Notice that each triangle shares the angle at E, that ED = EB since both are radii of the original circle, and that EF = EA since both are radii of the larger circle. Thus the triangles are congruent by SAS. This means ∠EBA equals ∠EDF, which is right, making ∠EBA right also. This allows us to apply the corollary to Proposition I.16 to say that AB must be tangent to the original circle.
This proposition is the converse to the corollary to Proposition III.16. That corollary says that a line drawn at right angles to a diameter must be tangent, and this proposition says that if we draw a diameter out to meet a tangent line, then they will meet at right angles. The proof is nearly identical to the proof of the first part of III.16.

This proposition is closely related to III.16 and III.18. It says that if we draw a line perpendicular to a tangent line at the point of tangency, then it must pass through the center of the circle. In other words, the part of the line that passes through the circle is a diameter.
The rest of Book III
We'll look at some of the remaining propositions in Book III, but not all of them.
Propositions I.20 and I.21 are about inscribed angles. These are angles where the vertices that form the angle sit on a circle, like in the example below. That angle opens up to an arc of the circle, the part of the circumference running clockwise from B to C. I find thinking about what it opens up to easier than how Euclid describes it. He describes it as sitting on the long arc that runs from B to C counterclockwise. That's the portion of the circle that it's inscribed into.
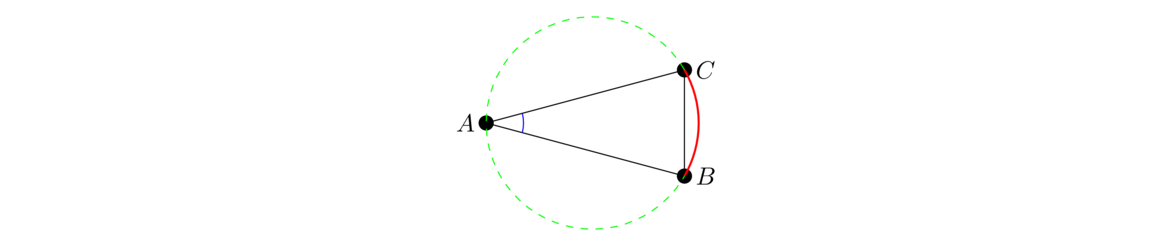
This is sometimes called the inscribed angle theorem or the central angle theorem. It says that if we have an inscribed angle ∠BAC like shown below on the left that opens up to arc BC and we have an angle ∠BEC based at the center of the circle that also opens up to arc BC, then the central angle is twice the inscribed angle. This works no matter where on the circle the inscribed angle is based, as shown below on the right.

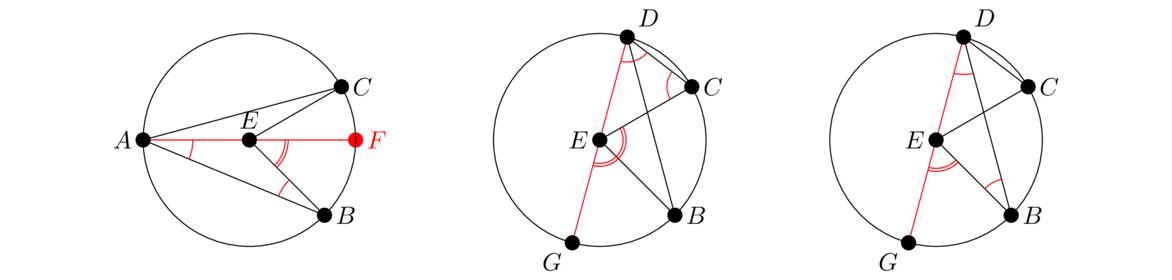
In the second case, we will look at the inscribed angle BDC shown above in the middle. We draw a diameter through DE. Since ED and EC are radii, △EDC is isosceles and ∠EDC = ∠ECD by Proposition I.5. By Proposition I.32, ∠CEG = ∠EDC+∠ECD = 2∠EDC since ∠ECD = ∠EDC. A similar proof shows ∠GEB = 2∠EDB. See above on the right. Our goal is to prove that ∠BEC = 2∠BDC. This follows from the fact that ∠BEC = ∠GEC–∠GEB = 2∠EDC–2∠EDB = 2∠BDC. That is, the wholes and one of the parts of ∠GEC and ∠EDC are in that 2 to 1 ratio, so the leftover parts must be in that ratio as well.
This says that inscribed angles that open up to the same arc must be equal no matter where their bases are, as long as they are in the same “segment.” For instance, ∠BAC and ∠BGC both open up to the same arc BC below, so they are equal. We haven't formally defined a segment, and won't, but we can think of the statement as saying that the angles need to be based on the same part of the circle in relation to the arc they open up to. For instance, in the figure below, A and G both need to lie outside the smaller arc BC. If one of them lies inside and the other outside, then the theorem wouldn't work.
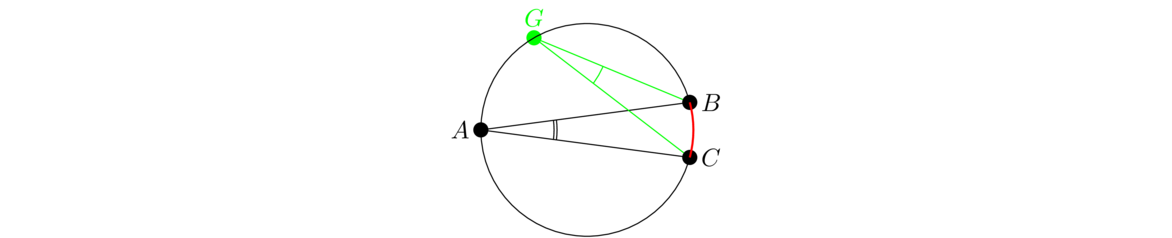
This says that if all four vertices of a quadrilateral lie on the same circle, then both pairs of opposite interior angles in the quadrilateral must sum to 180°. The part about it lying on the circle is important. An oddly-shaped quadrilateral, like shown on the right, might not have this property.

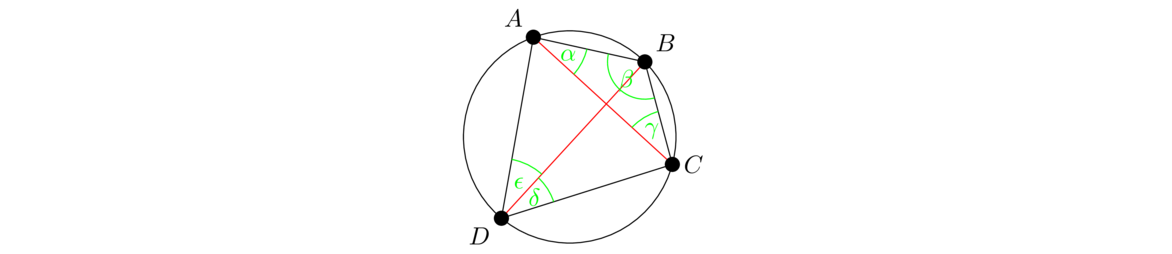
We will skip Proposition III.23 to III.25. Propositions III.26 to III.29 are relatively straightforward facts about arcs, the chord between the vertices that form the arc, and inscribed angles. Combining them, they say the following:
For instance, in the figure below, this says that if ∠BAC = ∠B′A′C′, then BC = B′C′ and arc BC equals arc B′C′. It also says that if BC = B′C′, then ∠BAC = ∠B′A′C′ and arc BC equals arc B′C′. And it says that if the arcs are equal, then ∠BAC = ∠B′A′C′ and BC = B′C′.
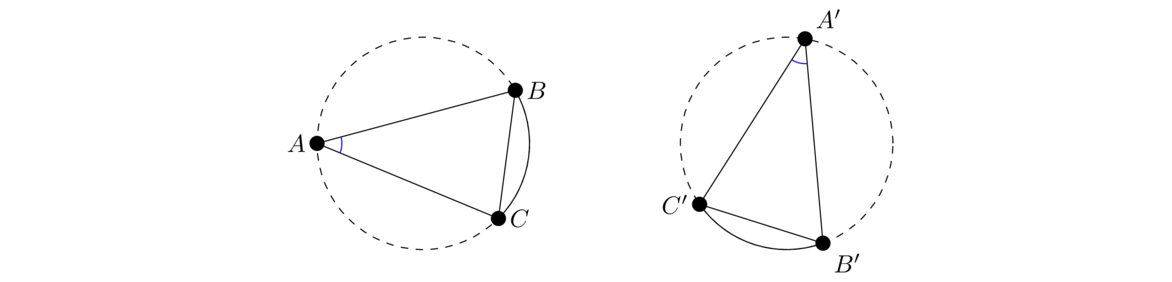
Proposition III.30 is a nice, quick application of the preceding. It is a construction that bisects a given arc of a circle.

This proposition is several statements in one. The first three parts are shown below. The first and most important part, also known as Thales' theorem, says that if an inscribed angle opens up to a diameter, then it must be right. If the inscribed angle sits on a part of the circle that is less than half the circle (and therefore opens up to an arc that is more than half the circle), then it will be obtuse. And, finally, if it sits on a part that is more than half the circle (and therefore opens up to an arc that is less than half the circle), then it is acute. We will only focus on these three parts. The part after the semicolon concerns the angles made between the circle itself and the lines that make up the inscribed angles. They are not hard to prove, but we will skip them.

To start, let the angle be ∠ABC with BC a diameter (meaning the angle opens up to a semicircle). We need to show that ∠CAB = 90°. Let E be the center of the circle and connect AE. Since EA and EB are radii, ∠EAB = ∠EBA by Proposition I.5. Let α denote the measure of both of those angles. Similarly, ∠EAC = ∠ECA. Let β be the measure of both of those. Then by Proposition I.32 on △ABC, we have α+β+(α+β) = 180°, which simplifies into α+β = 90°. This is what we want, since ∠CAB = α+β.
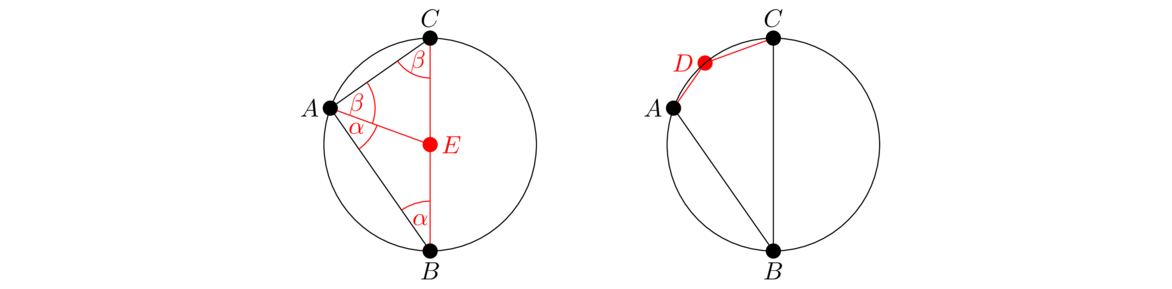
Next, let's look at the second and third cases by adding a point D between A and C as shown above on the right. By the proof above, we know that ∠BAC = 90°. And by Proposition I.17, ∠ABC < 90°, so that shows the third part of the proposition. By Proposition III.22, ∠ABC+∠ADC = 180°, so ∠ADC > 90°, showing the second part. We won't prove the rest of it, namely the part that follows the semicolon in the proposition statement.
It's tricky to see exactly what this is about. The picture below describes it. We have tangent line EF and angles α = ∠DAE and β = ∠DBF. The theorem states that α = β. We will prove the acute and obtuse cases separately.

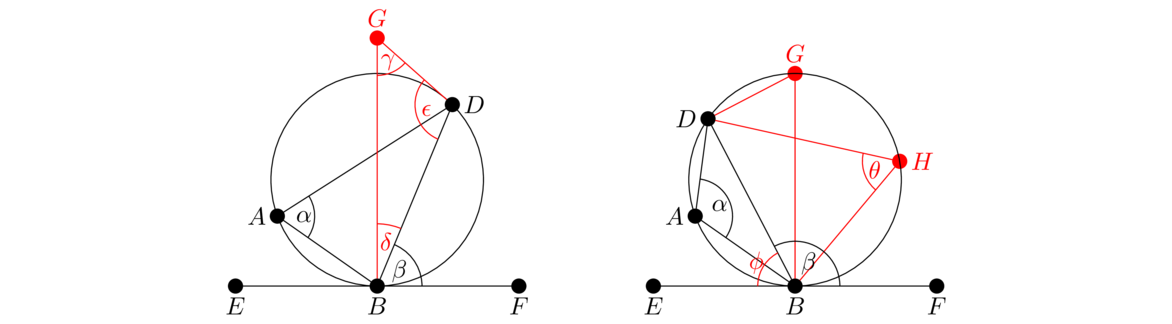
For the obtuse case, refer to the figure above on the right. Again, BG is a diameter. Choose H to be a random point on the opposite side of BG from α, and connect HB and HD. Let θ = ∠DHB and φ = ∠ABE. By the acute case, note that θ = φ. And φ+β = 180° by Proposition I.13, so θ+β = 180°. We also have θ+α = 180° by Proposition III.22. Putting these two equations together gives α = β.
This is sometimes called the intersecting secants theorem. It says that in the figure below, ab = cd. The proof is fairly long and complicated, and we will skip it, but there is a short proof that relies on similar triangles. Euclid doesn't get to similar triangles until Book VI.

These statements are converses of each other. Proposition I.36 says that if BD is tangent in the figure below, and if DA is a line intersecting the circle in two points, C and A, then BD2 = AD · CD. Proposition I.37 is the converse. It says that if that equation is true, then BD must be tangent. The proof of I.36 is much easier with similar triangles, so we will wait to prove it. The proof of I.37 is pretty straightforward, relying on I.36.
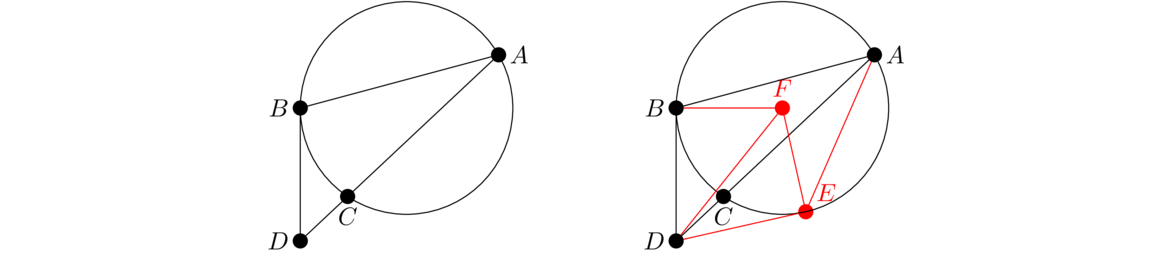
Book IV and a Little of Book VI
Introduction
Book IV is mostly about inscribing and circumscribing figures in other figures, with one of the figures being a circle. There are four possibilities:
- To inscribe a circle into a polygon is to draw a circle inside the polygon so that the sides are tangent to the circle.
- To inscribe a polygon into a circle is to draw the polygon so that its vertices lie on the circle and its edges lie inside.
- To circumscribe a circle around a polygon is to draw a circle around a polygon so that the vertices lie on the circle and the circle sits outside the polygon.
- To circumscribe a polygon around a circle is to draw a polygon around a circle so that its sides are tangent to the circle.
Shown below on the left is either a triangle inscribed in a circle, or a circle circumscribing a triangle. It all depends on which figure is there first. If we start with the circle and then draw in the triangle, we would say that the triangle is inscribed in the circle. If the triangle is there first, then we would say the circle was circumscribed on the triangle. Below on the right is a circle inscribed in a triangle or a triangle circumscribing a circle.
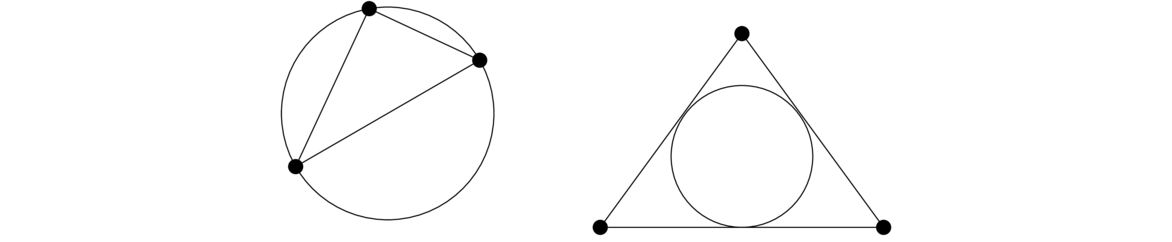
Centers of triangles
There are several different ways of defining the “center” of a triangle. A couple of them will be useful in Book IV. Here are the four:
- Incenter — Draw lines bisecting each of the three angles. The place all three lines meet is the incenter. This point also turns out to be equidistant from all three sides of the triangle.
- Circumcenter — Draw perpendicular bisectors to each of the three sides. The place all three meet is the circumcenter. This point turns out to be equidistant from all three vertices of the triangle.
- Centroid — Draw lines (called medians) from each vertex to the midpoint of the opposite side. The place where all three meet is the centroid. This point is the center of mass of the triangle, the point at which it would perfectly balance. The centroid is always 2/3 of the way from the vertex to the midpoint of the opposite side.
- Orthocenter — Draw lines (called altitudes) from each vertex perpendicular to the opposite side. The place where all three meet is the orthocenter.
In each case, it might not seem obvious that the three lines really do all meet at a single point, but it can be proven that they do. None of the proofs is particularly long or difficult, but we won't do them here. See below for examples of all four centers.

Some of these centers, specifically the circumcenter and orthocenter, can actually lie outside of the triangle. Below is an example showing the orthocenter lying outside an obtuse triangle.

For an equilateral triangle, it can be proved that all four centers coincide at the same point. And it can also be proved that this only happens for equilateral triangles. A fun fact is that if the triangle isn't equilateral, then the centroid, circumcenter, and orthocenter (but not necessarily the incenter) will lie on the same line, called the Euler line. Another interesting fact is the nine point circle theorem. It states that the following nine points all lie on the same circle: the midpoints of the three sides, the bases of the three altitudes, and the midpoints of the three line segments between the vertices and orthocenter. Both of these facts were not found until after Euclid.
Book IV

This proposition describes how to draw a given line segment so that both its endpoints lie on a circle. It might seem like we could just use Proposition I.3 to do this and not need a separate proposition, but I.3 only says that we can draw a line segment equal in length to the given segment, and it doesn't give us any leeway in how it's oriented.

Euclid's proof suffers from the same flaw as his proofs of Propositions I.1 and I.22. They all rely on finding an intersection point of two circles, but there is no axiom that guarantees there will be such an intersection. Further, it would be nice if something in the proof really made it clear why we can't fit a line larger than the diameter into the circle.
Propositions IV.2 to IV.5 are about the four variations of inscribing and circumscribing circles and triangles. The first one, Proposition IV.2, is where we are given a circle and a triangle, and we want to draw a copy of the triangle inside the circle. The copy won't be necessarily be the same size, but it will have the same shape, namely the same angles. It's similar in the sense of similar triangles. See Book VI for more on that concept.

Start by drawing a tangent line GH meeting the circle at point A. The use Proposition I.23 to copy one of the angles of the given triangle over to become ∠CAH, and use it again to copy another angle from the triangle to become ∠BAG. The points C and B that make up the angles are chosen to be where the lines making the angles hit the circle.
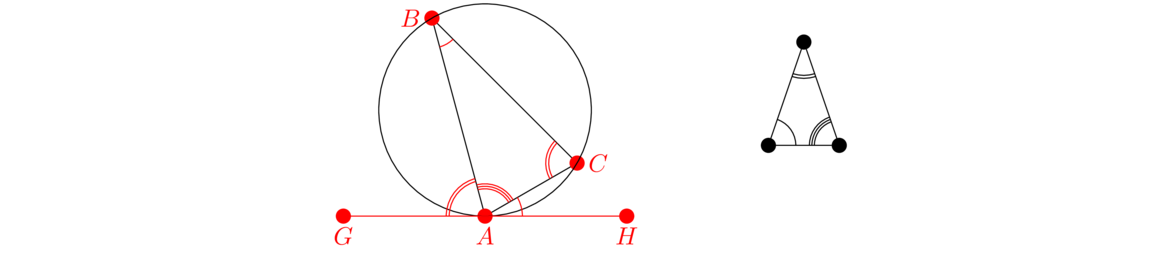
We claim that △ABC is equiangular with the given triangle. First, we have ∠BAG+∠BAC+∠CAH = 180° by Proposition I.13. And we have that ∠BAG plus ∠CAH plus the third angle of the given triangle are equal to 180° by Proposition I.32. Thus ∠BAC equals that third angle of the triangle. Then we can use Proposition III.32 directly to see that ∠CBA = ∠CAH and ∠BCA = ∠BAG, meaning that ∠CBA and ∠BCA match the other two angles of the given triangle. Thus we have inscribed a triangle equiangular with the given triangle into the given circle.

Let △DEF be the given triangle. Extend out line FE in both directions, creating angles DEG and ∠DFH. On the given circle, pick a random point B. Use Proposition I.23 to construct ∠BKA = ∠DEG and ∠BKC = ∠DFH. Use Proposition III.17 to draw tangent lines LM, MN, and LN, hitting the circle at points A, B, and C, respectively.
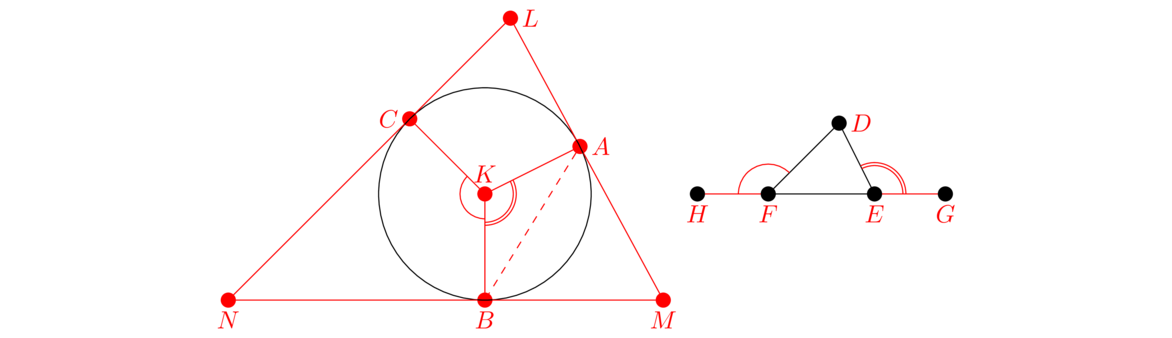
We claim that △LMN is equiangular with △DEF. To see why, look at quadrilateral KBMA. By Proposition III.18, tangent lines meet radii at right angles, so ∠KAM and ∠KBM are right. Line AB cuts KBMA into two triangles, and both triangles' angles sum to 180° by Proposition I.32, so the four angles in KBMA must sum to 360°. Two of them are right, as we've seen, so the other two must sum to 180°. This means ∠AMB = 180° – ∠BKA. Recall that ∠BKA = ∠DEG, and by Proposition I.13, ∠DEG = 180° – ∠DEF. Thus ∠AMB = ∠DEF. So the bottom right angles match in both the △LMN and △DEF. A similar proof works for the other two pairs of angles.


To see why, note that △BDF≅ △BDE by AAS, since each triangle consists of the equal bisected angle at B, a right angle, and the common side BD. Thus DE = DF. We have DF = DG for similar reasons. Thus E, F, and G all lie on the circle and the triangle. And because the angles at those points are right, we can use Proposition III.16 to conclude that the three edges of the triangle are tangent to the circle.
Note that the point D generated above is the incenter of the triangle. It is the center of the inscribed circle. The proof of the next proposition uses the circumcenter.

Use Proposition I.10 to bisect AB and AC, letting D and E be the midpoints of those lines. Then use Proposition I.11 to draw perpendicular lines to AB at D and to AC at E. Let F be the point at which they meet. It will turn out to be the circumcenter, and it can end up either inside, on, or outside the triangle. The case where F is inside the triangle is shown below.

Connect FA, FB, and FC. Then △FAD≅ △FBD by SAS since AD = BD, ∠FDA = ∠FDB = 90°, and FD is common. Thus FA = FB. Similarly, △FAE≅ △FCE, so FA = FC. Thus the circle with center F and radius FA will circumscribe the triangle. If F is on the triangle or outside the triangle, a very similar proof will work.
Note that Euclid never proves that the two perpendicular lines drawn will actually meet. Could they be parallel? The answer is no, and it can be shown pretty quickly that could only happen if the sides of the triangle are parallel, which is not possible.
The next four propositions are about the four combinations of inscribing and circumscribing circles and squares. We'll look at two of them.


Now draw a circle with center G and radius equal to GE. We now know that GE = GK = GH = GF, so E, K, H, and F all lie on the circle. And the lines of the square are tangent to the circle at those points by Proposition III.16 since the angles at those points are all right.
The triangle constructed by this proposition will have angles 36°, 72°, and 72°. You may have learned about 30-60-90 and 45-45-90 triangles before. This 36-72-72 triangle is another special one, though not as well known. If we take the two equal sides to be 1, the other base turns out to have length (√5–1)/2, which is a value closely related to the golden ratio. Euclid's proof of this proposition directly relies on several facts from Books I, III, and IV, including some that aren't used very often.
Start with some random segment AB. Use Proposition II.11 to construct a point C on AB such that AB · CB = AC2. The construct a circle with center A and radius AB. Use Proposition II.1 to fit a point D onto the circle with BD = AC. This is all shown below on the left. We claim that △ABD is the triangle we want. It's definitely isosceles since AB and AD are both radii. So by Proposition I.5, ∠B = ∠D. We now need to show that ∠D = 2∠A. Below on the right is an enlarged view of △ABD with various angles labeled.
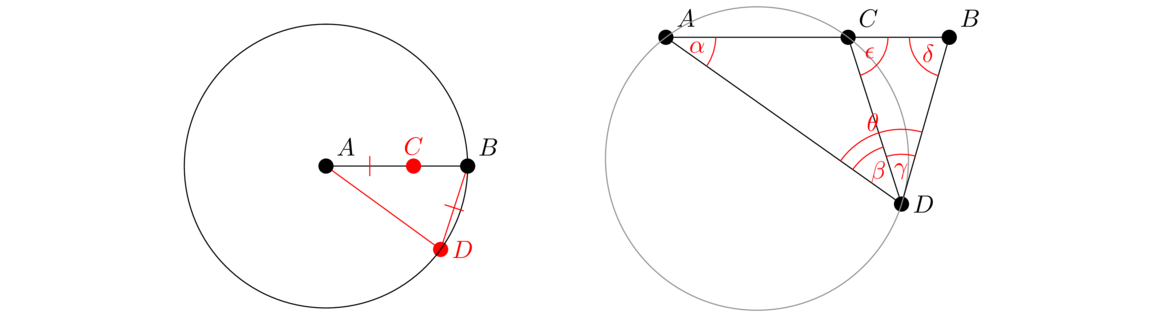 Connect CD and use Proposition IV.5 to construct a triangle that circumscribes △ACD. Points C and D were chosen such that AB · CB = AC2 and AC = BD, so we have AB · CB = BD2. This is now in the form that we can use Proposition III.37 to conclude that BD is tangent to the circumscribing circle. From this, we get that γ = α by Proposition III.32.
Connect CD and use Proposition IV.5 to construct a triangle that circumscribes △ACD. Points C and D were chosen such that AB · CB = AC2 and AC = BD, so we have AB · CB = BD2. This is now in the form that we can use Proposition III.37 to conclude that BD is tangent to the circumscribing circle. From this, we get that γ = α by Proposition III.32.
Using Proposition I.32, we get ε = α+β. Plugging in γ = α to this give ε = γ+β. But we also have θ = γ+β, so we get ε = θ. Next, since △ABD is isosceles, by Proposition I.5, θ = δ. Thus ε = δ, and that tells us △DCB is isosceles by Proposition I.6, meaning CD = BD. Thus, since BD was designed equal to AC, this makes CD = AC so that △CAD is isosceles. Thus by Proposition I.5 again, we have α = β. But we know that β = γ and θ is composed of β and γ, so θ = 2α, which is what we want to prove.
This proposition has allowed us to construct a 36-72-72 triangle, which is the key part in the next proposition about how to construct a regular pentagon.
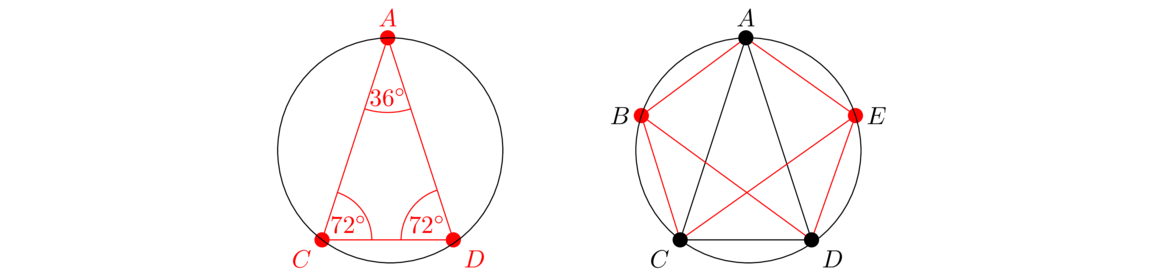
To see why, we first need to show that all the sides are equal. This comes from the fact that each side is opposite a 36° inscribed angle. In particular, CD is opposite the 36° angle at A, and all the others are opposite 36° angles at the base that come from bisecting the 72° base angles. Propositions III.26 and III.29 guarantee that the sides are equal because of this.
For the angles, let's say we want to show that ∠A = ∠B.
By Proposition III.27, this will follow if we can show that the arcs BCDE and CDEA are equal. These two arcs both share arc CDE, and if we remove it from each, what's left are arcs BC and EA, which are equal by Proposition III.28 since their corresponding chords are equal. A similar process can be used to show that ∠B = ∠C, ∠C = ∠D, and ∠D = ∠E.
Propositions IV.12, IV.13, and IV.14 are all the other variations of inscribing and circumscribing circles and pentagons. Proposition IV.13 is interesting in that its proof involves finding the incenter of a pentagon in a way analogous to how we find the incenter of a triangle. The angles created by connecting the incenter to the vertices of the pentagons turns out to be 72°. In general, we can create centers of any regular polygon. Those centers will always create an angle of 360/n degrees, where n is the number of sides in the polygon.
Proposition IV.15 shows how to construct a regular hexagon, and Proposition IV.16 is about how to construct a regular 15-gon. This brings up an interesting question: What are all the possible regular n-gons that we can create with a ruler and compass? Note that by regular we mean that all the sides are equal and all the interior angles are equal. This question was answered by Gauss in the late 18th century. He started by constructing a regular 17-gon. He was the first to do this, and of his many accomplishments, this was the one he said he was the most proud of. In the 2000 years between Euclid and Gauss, no one had constructed a new regular n-gon with a prime number of sides. Gauss then gave the general rule:
A regular n-gon (with n ≥ 3) can be constructed with a ruler and compass if and only if n is of the form 2kp0p1… pm, where k ≥ 0 and the pi are distinct primes of the form 22i+1.
Primes of this form are called Fermat primes after Pierre de Fermat, who studied them. The first few are shown below:
p0 = 220+1 = 2
p1 = 221+1 = 3
p2 = 222+1 = 5
p3 = 223+1 = 17
p4 = 224+1 = 65537
But then 225+1 = 4294967297 turns out not to be prime. In fact, nobody has ever found any more Fermat primes. Fermat had computed the first five above and conjectured all numbers of the form 22i+1 are prime, but it looks like he was spectacularly wrong. However, nobody knows for sure if there are any more. Numbers of this form get really huge really fast. For instance, 2210+1 already is 309 digits long, and 2220+1 is over 300,000 digits long. If any new Fermat prime were found, then it would give us a new regular n-gon (for some incredibly large number of sides).
Gauss's formula 2kp0p1… pm tells us that there are infinitely many regular polygons that are constructible. We can just keep multiplying by 2. For instance, starting with a regular triangle, we can create regular polygons with 3, 6, 12, 24, 48, 96, etc. sides. Note that in the formula, the primes have to be distinct. So we can create a regular 15-gon, using p1 = 3 and p2 = 5. But we can't create a regular 9-gon, since that would require doing p1 · p1, which are not distinct.
Book VI
Book VI is about similarity. Some of Euclid's proofs in Book VI rely on Book V. That book is all about ratios done geometrically. It's much easier for us to work with ratios using our modern algebraic tools, so we will just use algebra in our proofs. Euclid's definition of similarity is below.
Similar rectilineal figures are such as have their angles severally equal and the sides about the equal angles proportional.
We will only be interested in similar triangles here. The definition above tells us that there are two things that need to be true.
- The three angles in the one triangle must equal the three angles in the other triangle.
- The sides must be in proportion. In the figure below, this means that ab = de, ac = df, and bc = ef.

The proportions above can be written in different ways. For instance, ab = de can be rewritten as ba = ed, ad = be, or da = eb. We can use whichever form is easiest for the problem we're working on. We will only look at a couple of propositions from Book IV, starting with VI.2.
The first part of the proposition says that in the figure below if line DE is drawn parallel to the base, then ab = cd. The second part is the converse of the first.

 To compute these areas, draw altitudes with lengths e and f as shown above on the right. Then the area of AEB can be computed either as 12af or 12 ce. The area of AEB is 12(a+b)f, and the area of ADC is 12(c+d)e. Plugging these into the equation above gives
To compute these areas, draw altitudes with lengths e and f as shown above on the right. Then the area of AEB can be computed either as 12af or 12 ce. The area of AEB is 12(a+b)f, and the area of ADC is 12(c+d)e. Plugging these into the equation above gives
 This simplifies into a+ba = c+dc, which simplifies to 1+ba = 1 + dc. This is equivalent to ba = dc or ab = cd.
This simplifies into a+ba = c+dc, which simplifies to 1+ba = 1 + dc. This is equivalent to ba = dc or ab = cd.
The converse can be proved starting with ab = cd and essentially reversing the steps above to conclude that △DEB and △DEC have equal areas. Then use Proposition I.39 to conclude that the triangles are in the same parallels, meaning DB ∥ BC.
Recall that the definition of similar triangles has two parts: (1) the angles match up between the triangles, (2) the sides are proportional. This proposition says that as long as (1) is true, then (2) is true also.
Let △ABC and △DEF be given with ∠A = ∠D, ∠B = ∠E, and ∠C = ∠F. If it so happens that AB = DE, then by ASA, the two triangles are congruent and hence are similar (the ratios of sides between the triangles are all 1). Otherwise, by Proposition I.3, we can mark off a point G on AB such that AG = DE. Then use Proposition I.31 to draw line GH parallel to BC. This gives us a congruent copy of △DEF inside of △ABC. To see why, note that ∠AGH = ∠ABC by Proposition I.29, and ∠ABC = ∠DEF, so ∠AGE = ∠DEF. We also have ∠A = ∠D and AG = DE, so △AGH≅ △DEF by ASA.

We now have things set up to use Proposition IV.2. Let a = AG, b = GB, c = AH, and d = HC. Then by IV.2, ba = dc. This is algebraically equivalent to b+aa = c+dc. In other words, ABAG = ACAH. And using the triangle congruence, we get ABDE = ACDF. A similar argument shows ACDF = BCEF.
In any triangle, once we know two angles, we can find the third using Proposition I.32. Thus, we have the following important corollary to the proposition above:
Corollary to VI.4: If two triangles agree in two angles, then they are similar.
This proposition goes hand-in-hand with the previous one. Recall again that the definition of similar triangles has two parts: (1) the angles match up between the triangles, (2) the sides are proportional. The previous proposition says that if (1) is true, then (2) is true also. Proposition VI.5 says that if (2) is true, then (1) is true. This proposition is sometimes referred to as SSS for similarity. If all three sides are in proportion between the two triangles, then they are similar.
Let △ABC and △DEF be given with the sides in proportion. Use Proposition I.23 to make a copy of ∠B at E and a copy of ∠C at F, creating ∠FEG and ∠EFG. Note then that ∠C = ∠G by Proposition I.32.

So we have created an equiangular copy of △ABC along side EF. Thus by Proposition IV.4, ABBC = EGEF. Since our hypothesis is that the sides of △ABC and △DEF are proportional, we have ABBC = DEEF. Combining these facts gives EG = DE. Similar reasoning shows FG = DF. Then, since side EF is common, we have that △EFG≅ △EFD by SSS. Thus all the angles of △EFD match all the angles of △EFG, which in turn match all the angles of △BCA.
The last proposition we will look at is VI.6. It is the similarity equivalent of SAS. In particular, two triangles agree in an angle, and the sides flanking that angle are proportional, then the triangles are similar. The proof is quite similar to the proof of the previous proposition, so we will skip it.
Let △ABC be given with sides a = BC, b = AB, and c = AC, as shown below on the left. Use Proposition I.12 to draw a line from B perpendicular to AC. This creates two new right triangles △ADB and △BDC.
Note that △ADB and △ABC share ∠A and both contain a right angle, so the two triangles are similar by the corollary to Proposition VI.4. Thus the sides are proportional, and in particular we have db = bc, which is equivalent to b2 = cd. Likewise, △BDC and △ABC share ∠B and both contain a right angle, so they are similar as well by the corollary to Proposition VI.4. Thus we get ea = ca, which is equivalent to a2 = ce. Putting all of this together with the fact that c = d+e gives a2+b2 = ce+cd = c(e+d) = c2.
When we were looking at Book III, we decided to defer the proof of III.36 until we had covered similar triangles. Euclid's proof does not use similar triangles and is fairly involved. The similar triangle proof, on the contrary, is quite short. Recall that Proposition III.36 says that in the picture below, if BD is tangent to the circle, and AD passes through the circle at points A and C, then BD2 = AD · CD.
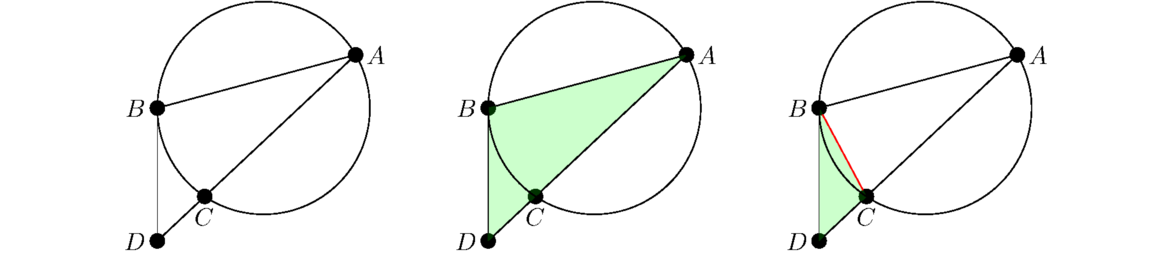
This equation is equivalent to ADBD = BDCD. We can prove this by showing that △ABD is similar to △BCD. By the corollary to Proposition VI.4, we just need to show that these two triangles are equal in two of their angles. One of those angles is ∠D, which is common to both triangles. For the other angle, we have that ∠CBD = ∠A by Proposition III.32. Thus the triangles are similar and the equation is true.