Tries
A trie is a type of tree used for storing text for easy retrieval. Trie is pronounced like “tree” or like “try,” depending on whom you ask. The name comes from the middle letters of “retrieval”. If we want to store the list of words AD, AN, ANY, CAB, CAN in a trie, it would look something like this:
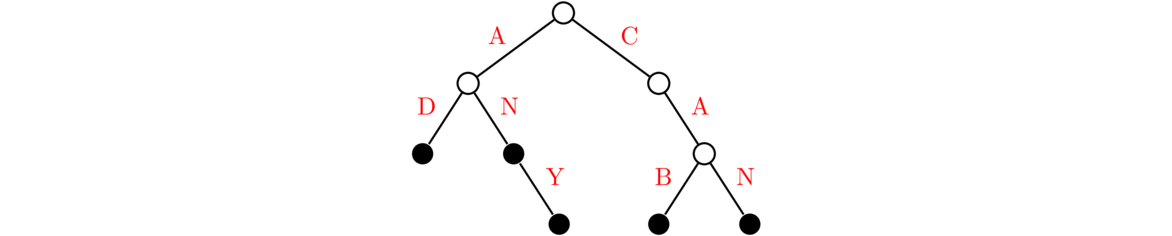
At the top of the tree is a root vertex. From it, we have branches for each starting letter of a word. The order of these branches doesn't matter. From there, each of those branches out for the second letters of the words. This branching process continues. In general, each edge of the trie represents a letter. Nodes represent the concatenation of all the letters leading from the root to the node. For instance, the leftmost node above represents the string “AND”. Leaf nodes and sometimes nodes in the middle of the trie store complete words. We use filled-in circles in the figure above to represent these nodes.
It's relatively quick to code up a trie class in Python. Here's one:
class Trie:
def __init__(self, is_word=False, links=None):
self.is_word = is_word
self.links = {} if links is None else links
def add(self, word):
n = self
for c in word:
if c not in n.links:
n.links[c] = Trie()
n = n.links[c]
n.is_word = True
It's a recursive class since each node in the trie is a trie itself. The class has a boolean variable to keep track of whether a node represents a complete word or not. To tell which nodes are adjacent to which, we use a dictionary whose keys are letters. In the trie shown earlier, the root node would have is_word set to False, and its links dictionary would have entries for a and c, each of those pointing to a subtrie. The add method starts at the top of the trie and works its way down, following the individual letters in the word and moving down the trie by following the links dictionary.
A common operation on a trie is to find all the words starting with a given prefix. Below is code we can add to our class to do that. The starting_with method walks down the trie following the characters in the prefix. It then calls the recursive all_below method that finds all complete words located at or below a given node.
def starting_with(self, prefix):
n = self
for c in prefix:
if c not in n.links:
return []
n = n.links[c]
return self.all_below(n, prefix)
def all_below(self, n, s):
M = [s] if n.is_word else []
if n.links == {}:
return M
for c in n.links:
M.extend(self.all_below(n.links[c], s+c))
return M
Once the trie is created, lookups depend only on the size of the word, not on the size of the dictionary. It's O(1) in terms of the size of the dictionary, and more specifically it's O(m), where m is the length of the word being looked up. This performance is comparable to hashing, and it can be either faster or slower than hashing, depending on a few factors. There is a cost for this speed, and that comes in the amount of memory required for the trie. There are various things that can be done to make tries more space efficient, though we won't consider them here.
Tries have a variety of uses. One use is for implementing an autocomplete feature. With that, you type in a few letters (a prefix), and you want all the words that start with those letters, which is exactly what the starting_with method returns. Another use is in IP routing, where the next hop a packet should take is based on the first so many bits (a prefix) of its destination IP address.