Topological Sort

One particularly important class of directed graphs are directed acyclic graphs, or DAGs. These are digraphs that contains no directed cycles; they are basically the digraph equivalent of trees**More properly, they are equivalent to forests, which are graphs whose components are trees (i.e., graphs that have no cycles and may or may not be connected).. The underlying graph of a DAG might not look like a tree, like the one shown below on the left, but when we take into account orientations, it behaves just like one.

The key property of DAGs is that we can order their vertices in such a way that there are never any backward edges, edges directed from a vertex later in the ordering back to a vertex earlier in the ordering. For example, in the graph above on the left, if we arrange its vertices in the order e, f, g, d, a, b, c, as shown on the right, we see that edges are always directed from left to right. This type of ordering is called a topological ordering.

This is important, for example, in scheduling. We often want to know which tasks need to be done before which other tasks. In a DAG, we can order the tasks so that a task's prerequisites are always completed before the task itself. For example,at Mount St.\ Mary's, certain CS classes need to be taken before others. For instance, CMSCI 120 Introduction to Computer Science I must be taken before CMSCI 125 Introduction to Computer Science II. We can make a DAG to represent courses and prerequisites by making the vertices be courses and using edges to indicate a course is a prerequisite for another. A digraph showing a few of the CS courses is shown below.

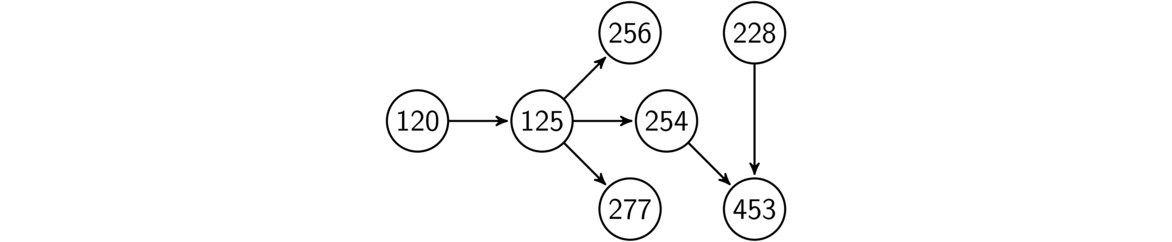
There is nice algorithm that finds topological orderings, called a topological sort. Recall that the degree of a vertex is the number of edges it is involved with. In a directed graph, the indegree of a vertex is the number of edges pointing into the vertex. Here is the basic idea of the topological sort: a vertex that has indegree 0 only has edges out from it. Therefore, it can safely go at the beginning of the ordering. Then delete that vertex (and all of its edges) and find another vertex of indegree 0. Put that vertex next in the order, delete it, and repeat until all vertices have been ordered. Here are the first three steps of the algorithm on the DAG above.

After this, d, a, b, and c are removed, in that order, giving us a topological ordering of e, f, g, d, a, b, c. Note that if there are multiple vertices of indegree 0, we can pick any one of them. There can be many possible topological orderings.

Will this always work? Since at every stage we choose a vertex v of indegree 0 in the graph that remains, we are guaranteed that no vertices that come later in the order can have edges directed backwards toward v. But then the main problem would seem to be that there might be no vertex of indegree 0 available. However, this is not the case. A DAG must always have a vertex of indegree 0. To see why, suppose there were no vertices of indegree 0. Start at any vertex v₁. It has indegree greater than 0, so there must be some edge v₂ → v₁. Similarly v₂ has indegree greater than 0, so there is some edge v₃ → v₂. We can keep doing this, but since the digraph has a finite number of vertices, we must eventually reach a vertex we have already reached, creating a directed cycle. But this a directed acyclic graph, so there can't be any cycles, and we have a contradiction. Note also that removing vertices from a DAG can't add any cycles, so at every step of the topological sort we are working with a DAG.

Below is some code that performs a topological sort.

from collections import defaultdict

class Digraph(dict):
    def add(self, v):
        self[v] = set()
    def add_edge(self, u, v):
        self[u].add(v)

def topo_sort(D):
    d = defaultdict(int)
    for x in D:
        for v in D[x]:
            d[v] += 1
            
    queue = [x for x in D if d[x]==0]
    order = []
    while len(queue) > 0 :
        x = queue.pop(0)
        order.append(x)

        for v in D[x]:
            d[v] -= 1
            if d[v] == 0:
                queue.append(v)

    return [] if len(order) < len(D) else order

The job of the first part of the function is to create a dictionary whose keys are the vertices of the graph and whose values are counts of edges pointing into each vertex (its indegree). The code does this using a useful Python object called a defaultdict. The default part of defaultdict is that the initial count will default to 0. We could do this with just an ordinary dictionary, but it would be a little messier.

After we build the dictionary, we create a queue that consists of all the vertices with indegree 0. We loop until we run out of vertices of indegree 0. At each iteration, we pop the first thing off of the queue, add it to the topological order, and then remove that vertex from the digraph. We don't physically remove it, but instead we simulate removing it by adjusting the indegrees of all its neighbors down by 1. This process might create some new indegree 0 vertices, which are added to the queue. The algorithm ends when we're out of indegree 0 verices. If we didn't end up adding all the vertices of the digraph into the topological order, then the graph must not have been a DAG, and we return an empty list. Otherwise, we return the topological order.