Red Black Trees
Binary search trees
Here is a quick refresher on binary search trees (BSTs). A binary search tree is a binary tree with the following property:
For any given node N, each element in its left subtree is less than or equal to the value stored in N and each element in its right subtree is greater than the value stored in N.
The tree below on the left is a BST. The tree on the right is not. The value 17 near the bottom right is in the right subtree of 18, yet 17 is smaller than 18. This can't happen. Further, there's a 16, which is greater than 14, to the left of 14, which also isn't allowed.
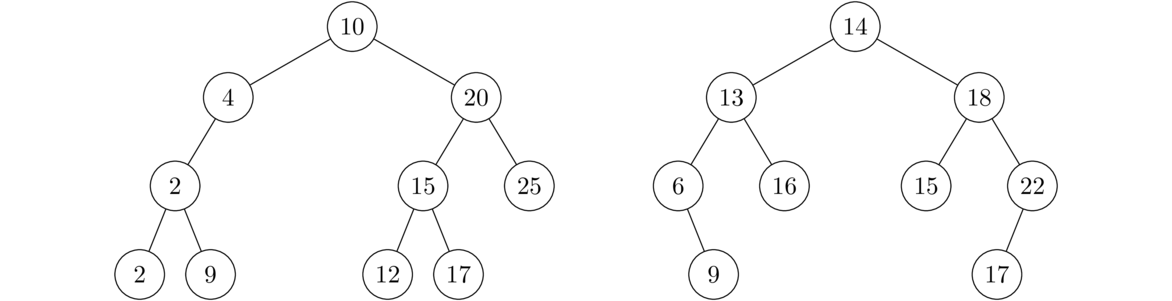
The purpose of a BST is to store data in a kind of sorted order that makes it quick determine if something is in the tree, quick to find the max and min, and quick to return the elements in order. It is also quick to add and remove elements. All of these operations run in O( log n) time, provided the tree is balanced.
But if we're not careful, a BST can quickly become unbalanced. This is where one side of the tree is significantly longer than the other. For instance, suppose we add the values 10, 9, 8, 7, 6, 5 to a BST in that order. The tree ends up not looking very treelike, as shown below.
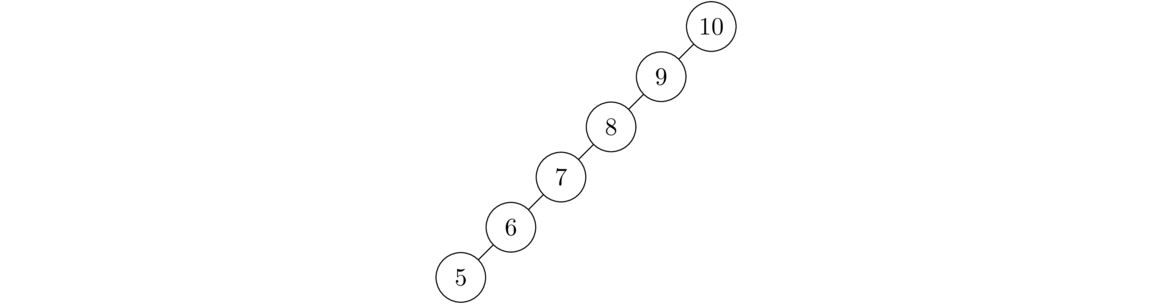
Since there's no branching structure here, the running times will degenerate from O( log n) to O(n). This is a real problem for BSTs since it is quite common to have real-life data initially be in sorted or reversed order before being added to a BST. There are a few tricks people have come up with for preventing this problem. The one we will cover is called a red-black tree.
Red-black trees
A red-black tree is a BST where each node is colored either red or black. The nodes have to meet the following properties:
- The root and the null leaves at the bottom of the tree are colored black.
- A red node cannot have a red child.
- Every path from the root to the null leaves at the end of the tree has the same number of black nodes on it.
Shown below is a red-black tree. In case you're viewing this in black-and-white, the red nodes have thicker boundaries. The null leaves are shown with x's. In a BST, the null leaves are used to indicate the end of the tree.
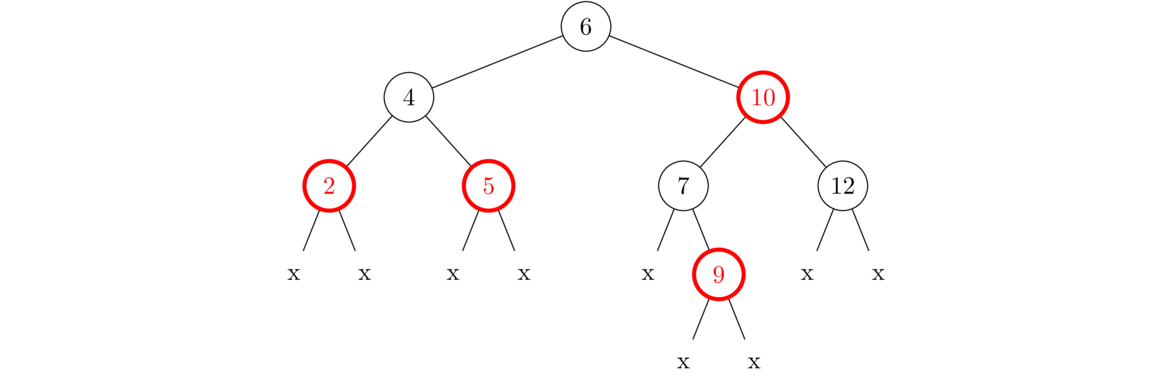
Notice that the three rules are satisfied because (1) the root and the null leaves are all black; (2) no red node has a red child (though red grandchildren are okay); and (3) every path from the root to a null leaf contains the same number of black nodes (namely exactly 3 black nodes in this tree, 2 if you don't count the null nodes). We will not show the null nodes in future figures, but know they are there.
Inserting things into a red-black tree
As we add new nodes to the tree, we will have to do certain operations to make sure the three red-black tree properties are preserved. This will keep the tree balanced so that one side never gets very much deeper than the other side. Some of the details below will get a little complicated. It would be good to skim over the rules now and refer back to them as we go over some examples.
Here is the procedure to add a new node:
- The very first node added to a red-black tree is black.
- Every other node is red when we first add it. We follow the ordinary BST rules when placing that node (go left if less than or equal, right otherwise).
- If the new node ends up having a black parent, then nothing needs to be done.
- If the new node has a red parent, then we will have to do some recolorings and rotations of elements in order to keep the properties of the tree satisfied.
For recolorings and rotations, there are several cases. In each of the cases below, N is the new node. Node P is the parent of N. Node G is the grandparent of N, and U is the uncle of N (namely the sibling of P and the other child of G). What is shown in the figures below is just a portion of the tree. Assume the tree continues above G. Assume also that A, B, C, D, and E in the figures are not single nodes, but entire subtrees (which is why they are shown with triangles instead of circles).
Note that we call N the “new node”. Usually it's the node that was just added, but it may be an old node that got colored red as a result of some other recoloring. It will always be the bottom node of a pair of adjacent red nodes.
This case is shown in the figure below. This rule works no matter where N is being inserted, whether it's on the left, in the middle or on the right.
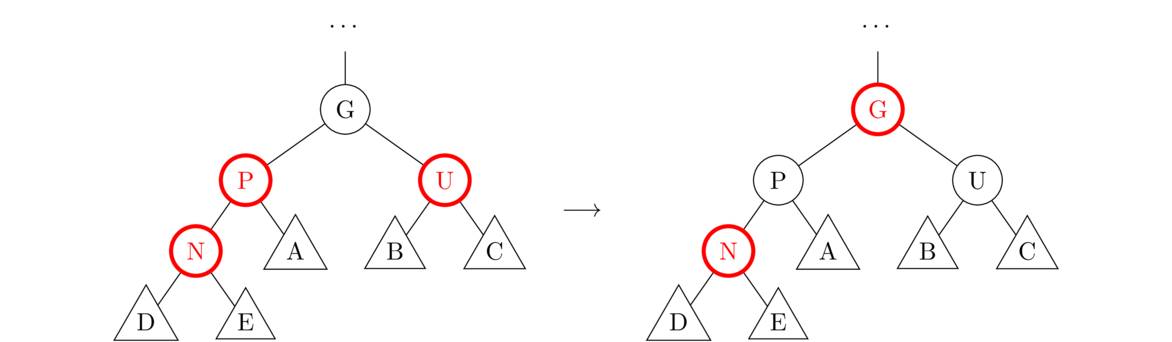

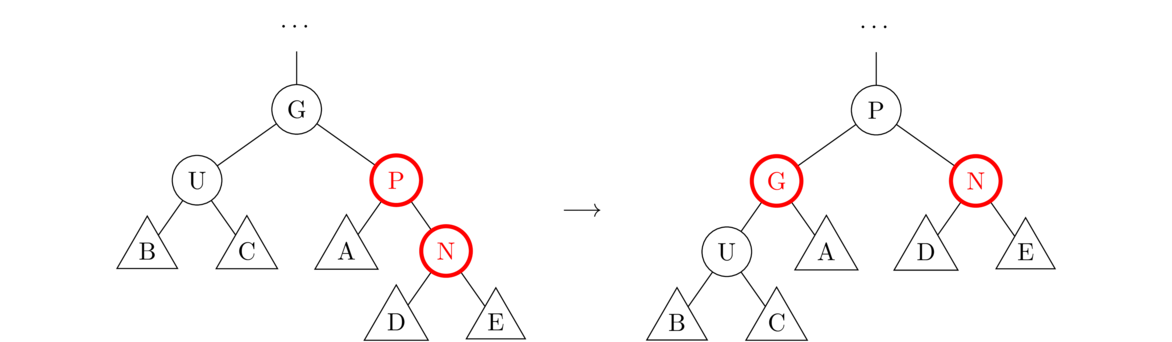
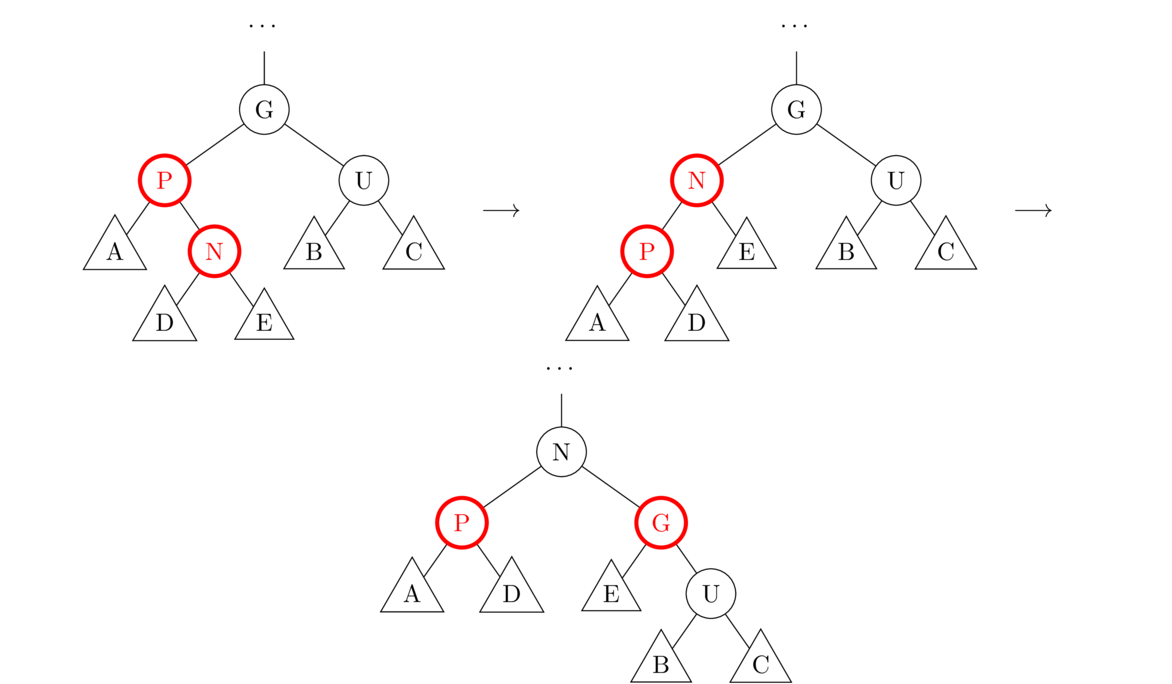
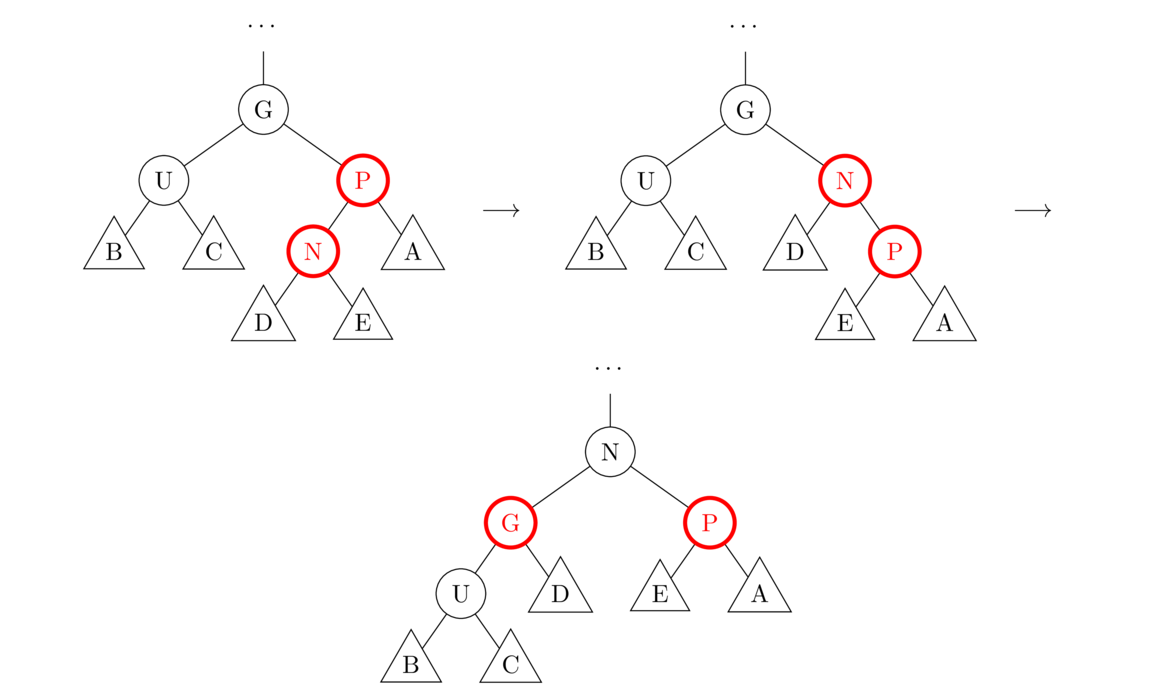
To summarize, all of these rules are used when we have to fix the situation of two red nodes in a row. If both the parent and uncle are red, then use Case 1. Otherwise, the other cases correspond to four possible configurations of P and N in relation to G: left-left (Case 2a), right-right (Case 2b), left-right (Case 3a), and right-left (Case 3b). The trick is to identify each of the parts N, P, U, G, A, B, C, D, and E (some of which may be null), and apply to appropriate operation.
An example
Let's look at an example where we add the values from 10, 9, 8, …, 1. For a regular BST, this is a bad case that leads to all the vertices being in a straight-line path. We'll see how the red-black tree, on the other hand, stays balanced.
Add 10. The first node added is always black.

Add 9. New nodes are always red. Since 9 is less than 10, it goes to the left of 10, like below. We only need to do recolorings and rotations if there are two adjacent red nodes, and that doesn't happen here, so there is nothing more to do at this step.

Add 8. It's a new node, so it's red, and it goes to the left of 9. Now we have a problem because we have two red nodes in a row. This is the left-left (Case 2a) configuration. That case tells us to rotate the three nodes clockwise as shown. In particular, 10 shifts down and right, 9 shifts up to the root, and 8 shifts up. Case 2a also tells us to recolor the old grandparent to be red and the new node to be black.

Add 7. It goes left of 8. This causes another problem with two reds in a row. Both the parent and the uncle are red, so we are in Case 1. That case tells us to recolor the parent and uncle to black, while making the grandparent red. In this case, the grandparent is the root, so it can't be red, so we turn it black.

Add 6. This is another left-left (Case 2a) configuration. We solve it with a rotation/recoloring.

Add 5. We are back in Case 1, so we fix the problem by recoloring the parent, uncle, and grandparent.

Add 4. This is a left-left configuration again.

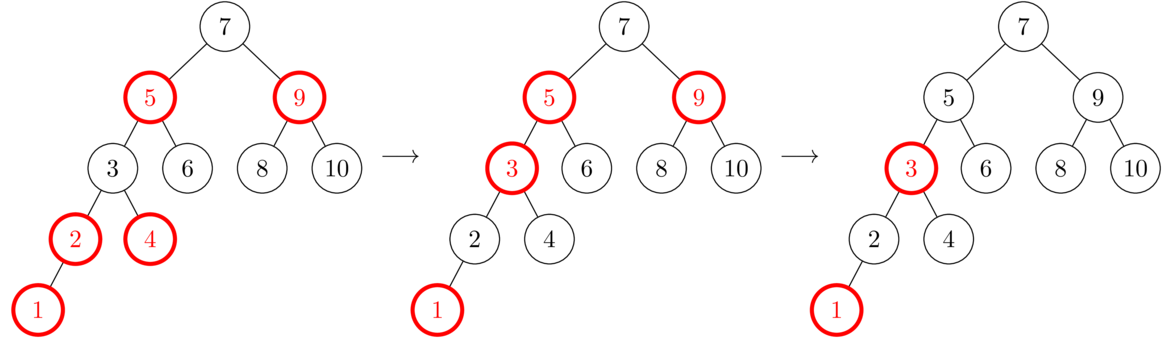
Add 3. This involves multiple steps. After adding 3, we are in a Case 1 situation, so we fix it by recoloring the parent, uncle, and grandparent as shown in the middle. But this causes a left-left (Case 2a) problem farther up the tree. We fix it with a rotation/recoloring. Referring back to the diagram for Case 2a, the 8 node plays the role of the A subtree, the 6 node plays the role of the E subtree, and the 4-3 subtree plays the role of the D subtree.
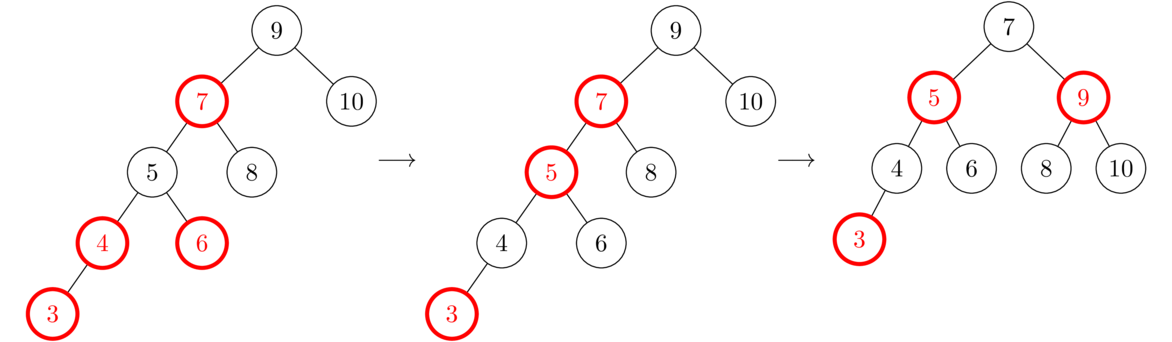
Add 2. Things are a little simpler here. It's a left-left configuration again, but only one step needs to be done.

Add 1. This is another multistep fix. After adding 1, we are in Case 1, so we fix that by recoloring. That recoloring causes another Case 1 problem farther up the tree, so we fix that. That will end up making the root red, so we finish by recoloring it to black.
At this point, notice that the tree is pretty well balanced. It's not perfectly balanced, as the left side goes two levels deeper than the right, but it's certainly better than an ordinary BST that would go 10 levels deep. Red-black trees can get a little out of balance, but never so bad as to affect the O( log n) running time for insertions. If you really need perfect balance, there is another approach to balancing BSTs called AVL trees, but we won't consider them here.
Another example
Suppose the tree looks like below on the left, where we are inserting 15. Following BST rules (left if less, right if greater), we find the right place to insert it is to the left of 20. New nodes are always inserted red, and inserting it causes no adjacent red nodes, so there's nothing else to do.

Let's now add 8 to the tree. It will go to the right of 5, like below on the left. We now have two reds in a row. Both the parent and the uncle of the inserted node are red, so to fix the problem, we use Case 1, which is to change the parent and the uncle to black and the grandparent to red.

Now let's say we want to add 18 into the tree. It will go to the right of 15, as shown below on the left. We have two adjacent red nodes in a left-right orientation, so this is Case 3a. Here N is 8, P is 15, G is 20, and the U is a null leaf. All the subtrees are null as well. According to Case 3a, we first do a rotation to turn this into a left-left configuration. This means that 18 and 15 swap places, with 15 going to the left of 18. This is shown in the second step below. Once we're in the left-left configuration, we use the rule from Case 2a to rotate and recolor, as shown in the third step below.

Now let's insert 9. It goes to the right of 8. This gives us two red nodes in a row. These are in a right-right orientation, so it's Case 2b. We have N=9, P=8, and G=5. The subtrees A, B, C, D, and E are all null, as is U, so all we have to do is rotate N, P, and G counterclockwise and recolor, as shown on the right.
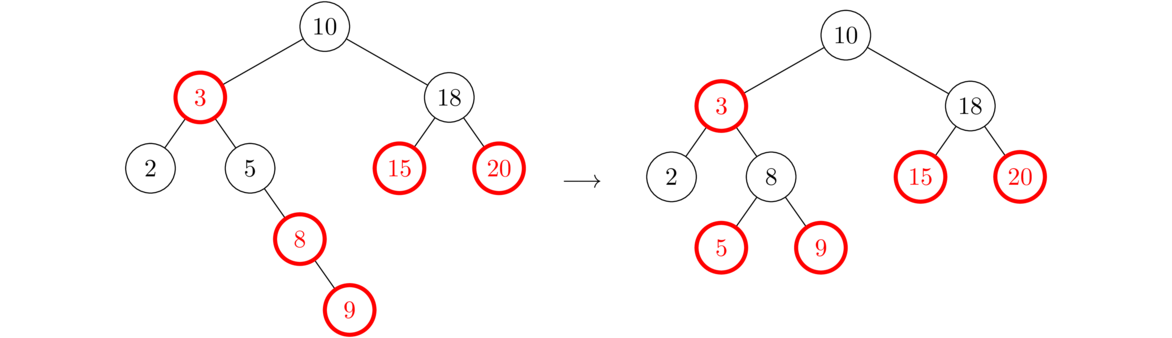
Finally, let's try adding 6. This is more complicated than the previous steps. First, 6 will go to the right of 5, as shown below on the left. This gives us two red nodes in a row, which we can solve with Case 1 since both the parent and the uncle of the new node are red.
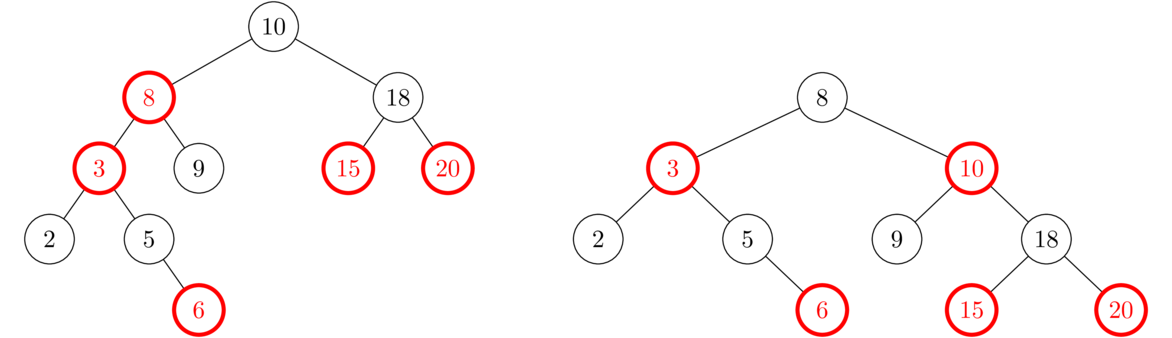
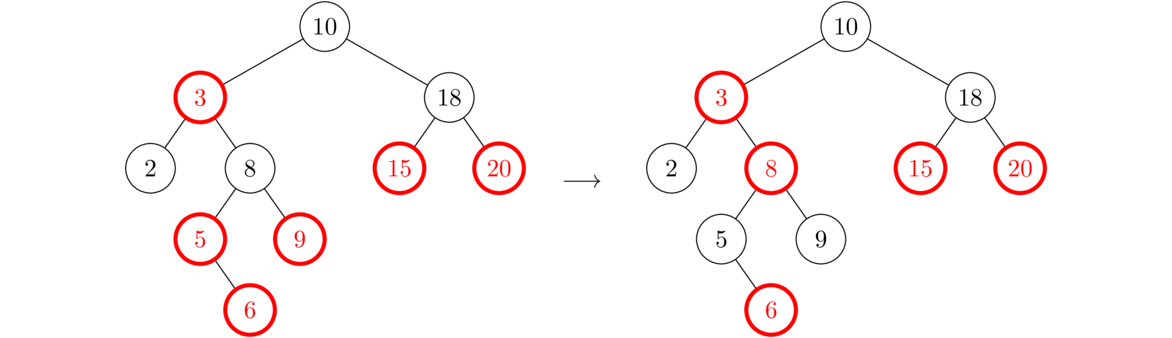 However, this creates a new problem farther up the tree as now 8 and 3 are adjacent red nodes. This is Case 3a, as the orientation is left-right. The figure for Case 3a is shown on the left, and the various part of the tree are labeled on the right according to Case 3a on the right.
However, this creates a new problem farther up the tree as now 8 and 3 are adjacent red nodes. This is Case 3a, as the orientation is left-right. The figure for Case 3a is shown on the left, and the various part of the tree are labeled on the right according to Case 3a on the right.
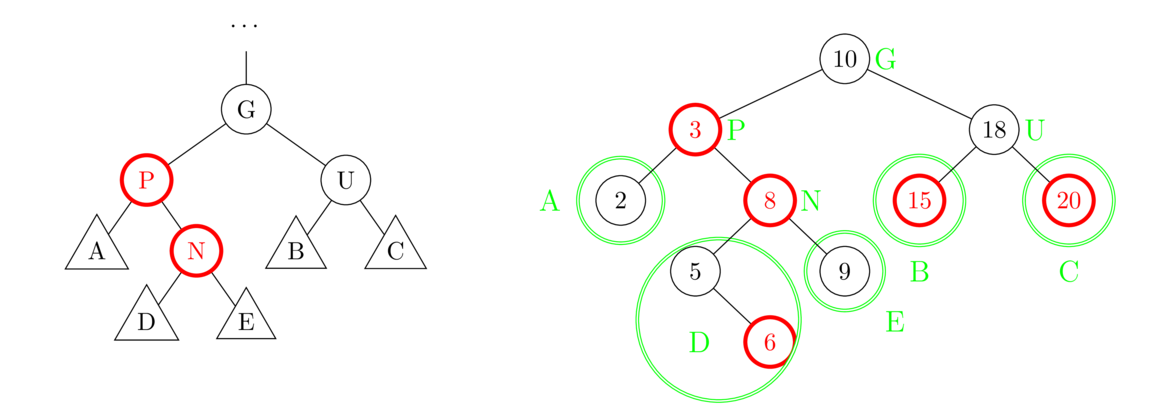
Below are the results of the two rotations from Case 3a. For the first rotation, 8 and 3 both rotate over to the left. After that, we need to figure out where their child trees A, D, and E should end up. The diagram from Case 3a tells us where, but we can also reason it out. The only way to keep all the BST properties satisfied is if A is the left child of 3, D is the right child of 3, and E is the right child of 8. For the second rotation, 3, 8, and 10 all move one position to the right, and the 9 subtree loses its home and moves over to the left of 10.
Conclusion
Why cover red-black trees? They are a well-known data structure that's good to know a little about. We won't go any more details about them. Vertex deletion and code for the operations can be found online if you're curious.