Huffman's Algorithm
A lot of data is sent in an 8-bit format, where each character is assigned to a numerical code (such as an ASCII code) from 0 to 255 (00000000 to 11111111 in binary). Characters that are used very often, like the letter e, take up 8 bits, and rarer characters like \"U also take up 8 bits. We could save a considerable amount of space with a variable-length encoding, where common characters are encoded with shorter binary strings, and we save the longer strings for rare characters.
We have to be a little careful how we do this. Let's look at a small example with letters a through f. Suppose we choose the following encodings:
| letter | encoding |
| a | 1 |
| b | 01 |
| c | 10 |
| d | 00 |
| e | 0 |
| f | 11 |
| letter | frequency | encoding |
| a | 35 | 01 |
| b | 15 | 100 |
| c | 9 | 1010 |
| d | 25 | 00 |
| e | 50 | 11 |
| f | 12 | 1011 |
Creating the codes
We will build up a binary tree. We start with a bunch of disconnected nodes, one for each character. The value stored in each starting node is its frequency. These starting nodes will all end up as leaves in the completed tree. After creating the nodes, we next look at all the nodes that don't yet have parents and select the two with the smallest values. We create a new node to be the parent of those two nodes, with the lesser node going as the left child and the greater node going as the right child. The new node's value will be the sum of the values of its two children. We keep this up as long as we can, until there is only one node left without a parent.
Here is an example. We start with one node for each letter, with a value equal to its frequency, like shown below.

At each step, we look at all nodes that have no parent. We take the two of these with the least values and combine them into a mini-tree with a new parent node whose value is the sum of the two nodes. To start, 9 and 12 are the least values. So we create a new node with value 9+12 = 21 and make 9 and 12 its children. The lesser value becomes the left child and the greater value becomes the right child.

The least values now are 15 and 21, so we create a new node with value 15+21 = 36 with 15 and 21 as its children. Note that at every step, the cheapest nodes could both be leaves, they could be one leaf and one non-leaf, or they could both be non-leaves.
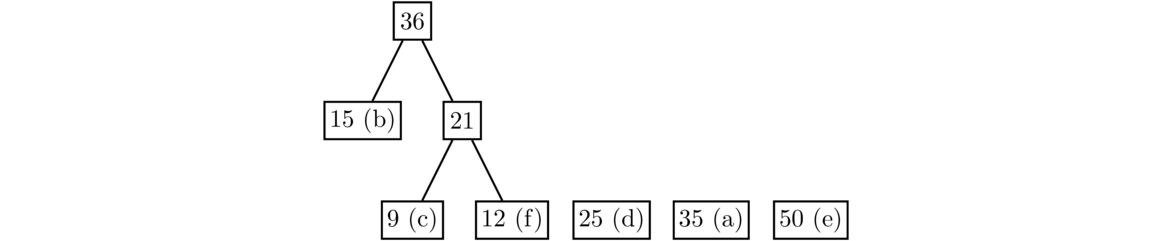
The two least values are now the leaves 25 and 35, so we combine them to create a new node with value 60.
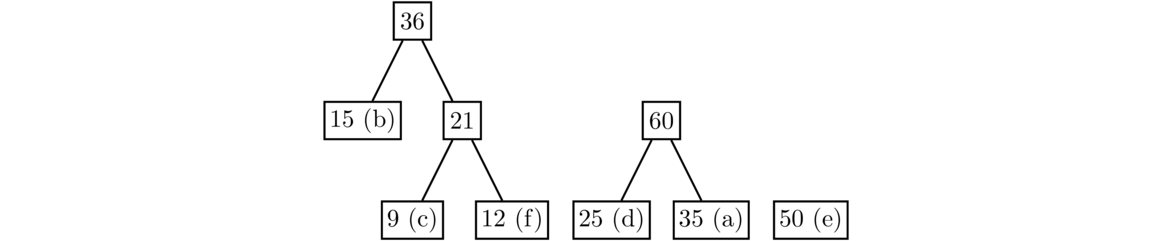
The two least values are now 36 and 50. Combine them to get a new node with value 36+50 = 86. This will add a new level to the tree.

The two least values are 60 and 86. After combining them, there is only one node left that doesn't have a parent, so we stop.
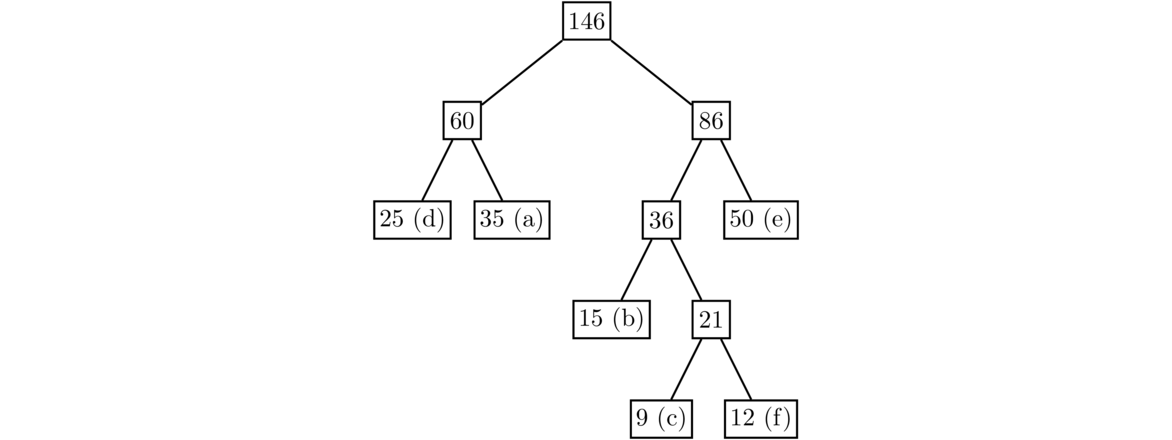
Finally, we label all the edges with 0 or 1 based on whether they go to a left child or a right child.

We can then read off the codes from the tree. For instance, the code for d is 00, since as we traverse the tree from the root down to the d node, the two edges we meet both have label 0. Similarly, the codes for a, b, c, e, and f are 01, 100, 1010, 11, and 1011, respectively. Notice that the higher frequency letters get shorter codes. This happens because the higher the frequency, the later it will get added to the tree, which means they will end up higher up in the tree, leading to a shorter path from the root and hence a shorter code.
When given some text like 101001100, we can use the tree to break it up. The first character is a 1, so we start at the top of the tree and go right, following the 1 branch. The second character is a 0, so we next go left. The third character is 1, so we go right, and the fourth is 0, so we go left. At this point, we have reached the end of the tree, being at the node representing c. So the first letter is c. We then move back to the root and do a similar process starting with the next character (the fifth in this case). It's a 0, so we move left. The next character is a 1, so we move right. We again arrive at a leaf, this time corresponding to the letter a. We then go back to the root and finish off the string, ending at the letter b. Thus 101001100 is broken into 1010 01 100, or cab.
Coding it
First, we will be building a tree, so it will be helpful to have a tree class. Since the class has no methods other than a constructor, we might consider instead using a dictionary or even a tuple to represent our trees. However, the benefit of a class is to allow us to use syntax like tree.left (instead of tree['left'] if we use a dictionary or tree[0] if we use a tuple).
class Tree:
def __init__(self, value, left, right):
self.value = value
self.left = left
self.right = right
Next we build up the tree. The function below has a parameter freq that is a dictionary or Python Counter object with keys equal to the letters and values equal to their frequencies (something like {'a':35, 'e':50}). To efficiently get the cheapest nodes at each step, we use a heap. Initially the heap contains the nodes corresponding to the letters. We insert these nodes as tuple of three things. The first is the value stored in the node. It needs to come first so that the heap sorts nodes based on their values. The second thing in the tuple will be discussed momentarily. The third thing in the tuple is a Tree object. This object stores a portion of the tree being built up.
The reason for the second part of the tuple has to do with when two nodes have the same value. When Python compares tuples, if the first entries are equal it will move on to the second item in the tuple. If we just use (value, tree), then it will try to compare trees and crash because it doesn't know how to compare some random tree object we created. A quick fix to that is to introduce a second value that is there simply to break ties. It's a counter that increases by 1 for each node. It is essentially an identifier for each node, which is why we've named it ident.
The main part of the algorithm pops the two cheapest nodes off the heap, creates a new node combining their values, and adds that to the tree. The loop stops when we are down to just one thing in the heap.
Be sure to import heap operations from Python's heapq library.
def build_tree(freq):
heap = []
ident = 0
for k, v in freq.items():
heappush(heap, (v, ident, Tree(k, None, None)))
ident += 1
while len(heap) >= 2:
a = heappop(heap)
b = heappop(heap)
n = (a[0]+b[0], ident, Tree(None, a, b))
heappush(heap, n)
ident += 1
return n
Once the tree is built, we need to get the codes. We do this by walking the tree and recording 0s or 1s depending on whether we take a step left or right.
Binary tree operations are usually easiest to do recursively, which is what we have done here. We use a parameter called prefix to keep track of the sequence of 0s or 1s. When we get to the end of the tree (a node with two null children), we add the prefix we've generated into our list of codes.
def walk_helper(tree, prefix, L):
if tree.left is None and tree.right is None:
L.append((tree.value, prefix))
else:
if tree.left is not None:
walk_helper(tree.left[2], prefix+'0', L)
if tree.right is not None:
walk_helper(tree.right[2], prefix+'1', L)
def walk(tree):
L = []
walk_helper(tree, '', L)
return L
Here is a little code to test out the algorithm.
d = {'a':35, 'b':15, 'c':9, 'd':18, 'e':50, 'f':12}#, 'g':12}
tree = build_tree(d)
for code, letter in walk(tree):
print(letter, code)
To see how well the algorithm compresses things, here is a little code. Copy and paste in some real text into the text variable to try things out.
from collections import Counter
text = 'copy and paste your own real text here...'
tree = build_tree(Counter(text))
L = walk(tree)
for code, letter in L:
print(letter, code)
count = 0
d = {letter:code for code, letter in L}
for t in text:
count += len(d[t])
print(count, 8*len(text))
Huffman's algorithm is a greedy algorithm, in that it always chooses the two cheapest things to combine. It is used in both the MP3 and JPEG compression algorithms.