B-Trees
Introduction
B-trees are close relatives of binary search trees (BSTs). See the notes on red-black trees for a quick refresher on BSTs if you need one. B-trees differ from BSTs in that each node can hold multiple values. This reduces the number of nodes in the tree, which turns out to be useful for trees stored on a hard drive, where the time to walk the tree from node to node is slow but accessing data within a node is fast. More on this later.
There is a parameter called m that specifies how many values can be in each node. Specifically, the maximum number of values in each node is m–1. We will only consider odd values of m in these notes. Below is a B-tree with m = 5. Notice that many of the nodes hold multiple values. With m = 5, no node can hold more than 4 values.

Notice also that it satisfies BST-like properties, where lesser values are to the left of the parent and larger values are to the right. But since there are multiple values in each node, it's a little different. For instance, look at the 1 6 node. It has three children. The values in the left child are all less than or equal to anything in the 1 6 node, and the values in the right child are all greater. But there is the middle child. It has values that are in between 1 and 6. Notice a similar thing happens with the children of the 30 80 90 node. The 40 50 child contains values that are between 30 and 80, and the 86 88 child contains values that are between 80 and 90.
Inserting into a B-tree
Here we will cover how to insert items into a B-tree. Like with red-black trees, the insertion operation is designed so that B-trees stay balanced, making all important operations O( log n). Here is an informal description of the rules. It's probably easier to understand with an example, so refer back to these rules as you work through the examples below.
- Start by finding the right place to insert the new node. It's similar to how a BST works, but a little different. At each node, you compare the new value with the values in the node and choose the appropriate branch. Specifically, if it is less than everything, take the leftmost branch; if it is between the first and second values, take the second branch from the left, etc.
- Other than with the very first value, new values will always go into an existing node, rather than creating a new node. So the insertion always stops at a leaf node, rather than creating a new node. Within each node, the values are stored in order.
- Nodes are allowed to hold up to m–1 values. If adding a value causes a node to fill up past that, then the middle value from the node will move out of the node and up the tree and become a part of its parent.
- This might cause the parent to become overfull, in which case the process is repeated for the parent.
- If there is no parent, then the middle value becomes its own new node.
- The remaining values from the overfull node will split into two equal-sized new nodes that are children of the node that now contains the old middle value.
- Any children of the overfull node may need to find new homes in the tree. They go in appropriate places as children of the two new nodes created in the step above.
An example
Here is an extended example with m = 3. We have a hypothetical sequence of integers to add to our tree (10, 20, 30, 15, 18, 50, 16, 40). There is a nice animation of B-trees at the following site that might help in seeing how everything works: https://www.cs.usfca.edu/~galles/visualization/BTree.html
Add 10. There's just one node, so nothing interesting yet.

Add 20. Since m = 3, nodes in this tree can hold up to 3–1 = 2 values, and 20 goes right into the existing node. In a B-tree, a new value is not initially added into a new node. It always goes into a preexisting node. And within the node we put things in order so that 10 comes before 20.
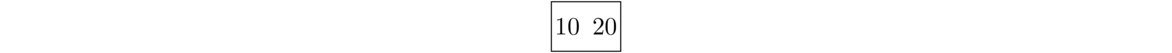
Add 30. We start by putting 30 into the existing node. At this point, the node is overfull. A B-tree with m = 3 fills up once it gets to 3 nodes. In B-trees, whenever a node gets overfull, the middle value from the node moves out of the node and into the node above it. There is no such node above right now, so we create a new node. The other two values break off to form their own new nodes.

Add 15. The tree now has two levels. We follow the usual BST rules with the exception that the new value goes into a preexisting node, not a new one. Here since 15 is less than 20, it goes to the left of 20. That node has only one thing in it, so there's room for 15 there.

Add 18. As 18 is less than 20, we go left of 20. Then we add 18 into the node at that location. This causes it to overflow. The middle value, which is 15, moves up out of the node to the next level above. There is room at the node there, so we add 15 into that node. The two other values that were part of the overflowing node go into new nodes that are children of the 15 20 node.
This result is now a little different from an ordinary BST since the root has three children: a left, a middle, and a right child. Note that the left child is less than both 15 and 20, the right child is greater than both, and the middle child's value lies between 15 and 20.

Add 50. Since 50 is larger than either value in the first node, we move right. There is room in the node at that point, so we add the value there.

Add 16. Here, 16 falls between the two values in the top node, so we go down the middle branch. There is room in that node, and we add 16 into it.

Add 40. This is the tricky step. To start, 40 is greater than both 15 and 20, so we go right and add it into the right child. This overflows the node. So the middle value 40 moves up to the next level, with 30 and 50 becoming new nodes. This is shown in the middle below.
This in turn creates an overfull node at the root. So we again take the middle value and move it up. Since there is nothing above, we create a new node for it. The two other values in the overfull node become new nodes. And we have to find homes for the 16 18 node and the 30 node. In order to maintain the properties of less being left and greater being right, we move 16 18 so that it is the right child of 15, and we move 30 to become the left child of 40.

A new example
Let's do another example, this time with m = 5. So now nodes can hold up to 4 values and once a node gets to 5 values, we have to break it up.
Add 10, 30, 50, and 20. Since nodes can hold 4 values, these four steps fill up the root node until it looks like below.

Add 40. This overflows the node. The middle value, 30, moves up a level. There is nothing at that level, so we create a new node for it. The other four values break into two equal-sized children of the new node.

Add 80 and 90 and 95. These values are all greater than 30, so they go into the right child. The addition of the last value, 95, causes the node to overflow. The middle value, 80, moves up a level, and the remaining values split into two new children as shown below. Notice in particular that 40 50 goes as the middle child and 90 95 goes as the right.

Add 2, 3, and 4. This is a lot like the previous set of additions except these values all go into the left child until they cause it to overflow. The middle value, 4, moves up a level. The remaining values split into two equal-sized nodes. Note in particular, where all the nodes fit underneath the parent.

Add 14, 15, and 16. These values are all between 4 and 30, so they go into the second child from the left. Eventually they cause it to overflow. This creates the tree on the right, where the root is now as full as it can get.

Add 0, 0, and 1. These all go into the left child, as shown below.

This overflows the left child. The middle value from that node moves up, and we break the remaining values into two nodes, as shown below.

This causes the root node to overflow. The middle value, 15, moves up and becomes its own node. The remaining values split into two equally-sized nodes, 1 6 and 30 80. All of the children of the old root now need new homes. The lesser-valued children become children of the 1 6 node, and the larger children become children of the 30 80 node. See below.

Why B-trees are important
The use-case of a B-tree is when you have a very large amount of data that you want to store in a sorted order. Specifically, the data is too large to fit in RAM and needs to be stored on a hard drive or over a network. A hugely important example of this is storing indices into a database.
The two main types of hard drives are HDDs and SSDs. Reading a random value from an SSD is around 20 times slower than reading from RAM and reading from an HDD is around 20,000 times slower. Reading from a network can be even slower, especially if there are long distances involved. So if each node of a BST is stored on a hard drive or network, each time you move from one node to a next when searching a BST, that's a lot of time to spend. B-trees considerably lessen the number of nodes that need to be checked.
Further, the way reading things from hard drives, especially HDDs, works, the slow part is finding the item on the drive. Once you are there, reading adjacent values is fast. In a B-tree, the values in a node would be stored next to each other, so reading an entire node is fast. The slow part is finding the node.
Just like with red-black trees, we won't worry about deletion or coding things. Please see the nice animations at https://www.cs.usfca.edu/~galles/visualization/BTree.html to help understand B-tree insertions.