Stream Ciphers
The classical cryptographic ciphers we've covered were meant to be used by humans by hand. Since humans are slow and mistake-prone, those ciphers are limited in what they can rely on from their users. This is part of what makes them breakable (except for the one-time pad, of course). In modern cryptography, computers, which are fast and mostly mistake-free, do the enciphering and deciphering, allowing us to design complex methods that are hard to break.
Exclusive or
Computers work in binary and are fastest when dealing with purely binary information, so much of modern cryptography uses binary. The most important binary operation in cryptography is the exclusive or, usually denoted as XOR or by the symbol ⊕ . Here are the rules for it:
0 ⊕ 0 = 0
0 ⊕ 1 = 1
1 ⊕ 0 = 1
1 ⊕ 1 = 0
The first three of these four rules are just like ordinary addition. The only weird thing is the last rule: 1 ⊕ 1 = 0. It's like arithmetic modulo 2 if you know what that is. Also, if we think of 0 as false and 1 as true, the rule is that p ⊕ q is true if one or the other of p and q is true, but not both. Here is a typical calculation:
| 1 | 0 | 1 | 1 | 0 | |
| ⊕ | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
The reason why XOR is so important is that if you XOR by the same thing twice, you get back to where you started. For instance, here is a simple encryption scheme: We have a binary plaintext P and a binary key K. Encrypt by doing C = P ⊕ K. To decrypt we do the same operation, XOR-ing with the key: P = C ⊕ K. So encryption and decryption are done the same way.
Below is an example with P = 1010 and K = 1001. On the left is the encryption and on the right is the decryption.
| 1 | 0 | 1 | 0 | |
| ⊕ | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | |
| ⊕ | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
If you don't mind a little math, the reason this works is pretty simple. Since 0 ⊕ 0 = 0 and 1 ⊕ 1 = 0, whenever you XOR something with itself, you get 0. So since C = P ⊕ K, we have
Stream ciphers
If we take our simple XOR encryption scheme and make sure the key K is chosen perfectly randomly and only used once, then we would have a binary one-time pad, which is unbreakable. But generating true random numbers is time-consuming and difficult. If we instead use a pseudorandom number generator (PRNG), then we have what's called a stream cipher.
Here's how it works. We start with a key, which could be binary, a string, or whatever. We then use it to “seed” the PRNG. This seed is a starting value for the PRNG, and then the PRNG generates random bits (0s and 1s) based off the seed and some mathematical algorithm. The random bits it generates are called the keystream.
To encrypt and to decrypt, we XOR each bit of the plaintext with the corresponding bit of the keystream, just like with the XOR cipher of the previous section.
The pseudorandom number generators (PRNGs) built into most popular programming languages can be used to create a simple, but insecure, stream cipher. For example, here is a really short Python stream cipher.
import random
def encrypt_decrypt(plaintext, key):
random.seed(key)
return bytes([b ^ random.getrandbits(8) for b in plaintext])
ciphertext = encrypt_decrypt(b'secret', 'some key')
print(ciphertext)
print(encrypt_decrypt(ciphertext, 'some key')
Notice that the same method is used to encrypt and decrypt. That method seeds the random number generator with a value determined by the key string. The calculation uses the ^ operator, which is used to denote XOR in most programming languages. There is also a little Python stuff to handle converting things into binary.
This simple cipher is not all that bad, but any competent cryptographer could break it because Python's random number generator is not cryptographically secure. It's not designed for that purpose. Below is a much stronger random number generator used in the RC4 stream cipher.
K = [120, 38, 244, 18, 97, 183, 22, 203]
S = list(range(256))
j = 0
for i in range(256):
j = (j + S[i] + K[i%len(K)]) % 256
S[i], S[j] = S[j], S[i]
i = j = 0
key_stream = []
for k in range(100):
i = (i + 1) % 256
j = (j + S[i]) % 256
S[i], S[j], = S[j], S[i]
t = (S[i] + S[j]) % 256
key_stream.append(S[t])
The first line of the code is the key used to seed the PRNG. The rest of the code generates 100 keystream bytes. It's neat that just a few lines of code like this generates random numbers that are pretty secure (but not totally secure as we'll see).
Reusing keys
Just like with the one-time pad, reusing the keystream of a stream cipher makes it very breakable. For example, suppose the same keystream has been used for two messages, where we know the both the plaintext and ciphertext of one message, and we have the ciphertext of another. This is demonstrated in the example below.
| Plaintext 1 | ? | ? | ? | ? | ? | ? |
| Keystream | ? | ? | ? | ? | ? | ? |
| Ciphertext 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| Plaintext 2 | 1 | 0 | 0 | 0 | 1 | 1 |
| Keystream | ? | ? | ? | ? | ? | ? |
| Ciphertext 2 | 1 | 1 | 1 | 0 | 0 | 0 |
It's not hard to work backwards to figure out the keystream since we have Plaintext 2 and Ciphertext 2. In fact, we can just XOR Plaintext 2 and Ciphertext 2 to figure out what the keystream is. Then we can XOR the keystream with Ciphertext 1 to figure out Plaintext 1. It's a good exercise to practice this. The keystream will come out to 011011 and Ciphertext 1 will come out to 010110.
Even if we only have the two ciphertexts and not Plaintext 1, we can often still get interesting information just by XOR-ing the two ciphertexts together. Mathematically, here's what we get by doing this:
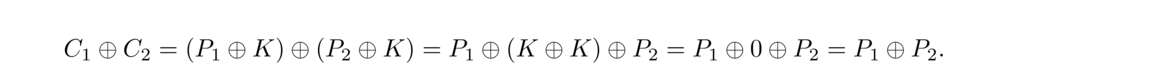 Now, P1 ⊕ P2 will be a jumbled mush of the two plaintexts, but often we can see parts of one or the other plaintext show up in the clear. If one of the plaintexts has a long run of zeroes, the other plaintext will be the only thing that contributes ones to P1 ⊕ P2.
Now, P1 ⊕ P2 will be a jumbled mush of the two plaintexts, but often we can see parts of one or the other plaintext show up in the clear. If one of the plaintexts has a long run of zeroes, the other plaintext will be the only thing that contributes ones to P1 ⊕ P2.
For example, below are three images. The image on the left is a black and white image of a garden, and in the middle is a black and white image of a kitchen. Both images were reduced to just two colors, black (0) and white (1). Then the two images were XOR-ed together. The result is a jumbled mess, but we can clearly see features coming through from both pictures.

Uses of stream ciphers
Stream ciphers are one of the most widely used types of modern cryptography. They can encrypt and decrypt huge quantities of data quickly. They are very secure if used with a secure PRNG.
Stream ciphers are a very good approximation of a one-time pad. One major weakness of the one-time pad is that the key needs to be as long as the message itself. With a stream cipher, the key can be pretty short, usually a few dozen bytes. That key is used to generate the keystream, which takes the place of the one-time pad's giant key. The short key used to generate the keystream can be easily shared by two parties using the key exchange protocols we'll cover later.
Another major weakness of the one-time pad is that the true random numbers it requires are very slow to generate. Pseudorandom numbers, on the other hand, can be very quick to generate. However, when we give up true randomness, we lose the perfect security of the one-time pad. But if the PRNG is really good, then the keystream can be nearly as good as true random.
Probably the most well known stream cipher is RC4. It's not much used anymore because various weaknesses were found in it, but in its heyday it was used in TLS to encrypt web traffic and in the WEP standard for Wi-Fi. WEP has a particular weakness that causes keystream reuse, which makes it very breakable. RC4, as used in TLS, is much stronger than the version in WEP. However, there are very slight biases in its PRNG. It has a tendency to generate more 0s than 1s in particular positions in the keystream. When large amounts of data are encrypted with RC4, statistical techniques could take advantage of that bias to decrypt the data.
As of this writing, probably the most widely used stream ciphers are called Salsa20 and ChaCha20. They are part of TLS. The block ciphers we'll cover elsewhere can also be turned into stream ciphers.