Memory
Types of storage
Here are some important ways of storing data, organized from fastest to slowest:
- CPU registers — These are small memory locations, usually on the CPU, that hold single values. These are the fastest type of memory on a computer. Because space on a CPU is limited and valuable, there are not many registers, typically anywhere from a few dozen to a few hundred registers, depending on the architecture. Many of these registers are for very specific purposes, but some can be used to hold data, especially variables that are very frequently used.
- CPU cache — This is very fast memory that is close to the processor core. There are multiple types: L1, L2, and L3. L1 is the fastest, closest to the processor core, but also the smallest. L2 is a little farther away, slower, but larger. L3 is the farthest away, the slowest, but the largest.
In order to be fast, L1 cache must be small since the larger the cache is, the longer it takes to find items in it. Typical CPUs have 16 to 64 kilobytes of L1 cache, though more can be had on expensive processors. Often each core of a multicore processor will have its own L1. L2 is typically several hundred kilobytes in size up to a few megabytes. Like with L1, each core will often have its own L2 cache. L2 is typically around 4 times slower than L1. L3 cache runs from a few megabytes in size up to as much as 256 MB. It is often shared between multiple cores and is considerably slower than L1 and L2, though still much faster than RAM.
- RAM (random access memory) — Also called main memory, RAM is the primary holding place for data while a program is running. Typical computers in 2021 have anywhere from 2 GB of RAM up to around 128 GB.
- Disk drives — There are many types of disk drives, though the two we are interested in here are hard disk drives (HDDs) and solid state drives (SSDs). HHDs are mechanical devices, a little like record players, with a spinning disk and a read head. Positioning that read head is a slow process that takes a few milliseconds. SSDs store data electronically and are considerably faster than HDDs, though considerably slower than RAM. HDDs and SSDs are persistent storage, which means they can store data even when the power is turned off. RAM is nonpersistent storage. Whatever is in RAM is lost when the power is turned off.
- Cloud storage is the slowest option because it usually takes anywhere from a few milliseconds to hundreds of milliseconds to transfer a packet over a network. That time varies based on distance and on how busy the network is. The speed of light is around 186,000 miles per second, which gives a definite limit to the time it takes to access cloud storage. For instance, a round trip across the US and back is about 6000 miles, and 6000/186000 comes out to about 32 milliseconds. This means that asking for and retrieving data from cloud storage 3000 miles away can never be faster than 32 milliseconds. And in fact, signals in copper and fiber optic cables travel at only around 2/3 the speed of light, so 48 milliseconds is a more practical lower limit. Routers take time to process packets, and they may be bogged down handling lots of other packets, so 48 milliseconds is an optimistic estimate.
The site https://colin-scott.github.io/personal_website/research/interactive_latency.html has a nice graphical display of the “latency numbers every programmer should know.” Based on their 2021 figures, here is a table showing how fast each type of memory is.
| Registers | L1 Cache | RAM | SSD | HDD | Cloud |
| 1/3 ns | 1 ns | 100 ns | 16 μs | 2 ms | 150 ms |
The lesson here is that RAM is around 100 times slower than cache memory, SSDs are about 10 to 20 times slower than RAM, HDDs are about 100 times slower than SSDs, and accessing cloud storage is typically about 10 times slower than an HDD. These figures are all rough estimates as there is a lot of variability in hardware.
Memory allocation
Operating systems and other programs often need to hand out memory to processes and other things that need it. For example, when you use the C malloc function, that memory is given to your program from a memory allocation program. The basic idea is that there is a pool of free memory and the allocator gives some of it out in response to requests. When the requester is done with the memory, it goes back to the free pool. We'll look at an example below with a free pool of 100 units of memory. Assume that allocations must be contiguous.

Suppose a request from process A comes in for 15 units. The allocator could give A any 15-unit chunk it wants, but let's say it choose the region from location 0 to 15, like shown below.

Maybe next two more requests come in: 5 units for B and 20 for C. Then memory would look like below.

Then suppose that B frees its memory. It goes back to the free pool, and memory looks like below.

After a lot of allocations and deallocations, memory gets to have Swiss cheese look, like below. This is called fragmentation.

The main issue with fragmentation is the combined free area might actually be pretty large, but if it's broken up into a bunch pieces, then there might not be a big enough chunk available to satisfy requests. One solution to fragmentation is to periodically defragment memory by moving the allocations around so they are all next to each other. But this isn't used very often since it's very slow. Having your computer periodically freeze for a while to defragment RAM would not be a pleasant user experience. On a related note, some HDDs benefit from occasionally being defragmented, a process that can take hours.
There are two types of fragmentation: external and internal. External fragmentation is what is shown above, where after many allocations and deallocations, the free slots are small and widely spread out. Internal fragmentation happens when an allocator gives out more memory to a process than the process needs. Whereas external fragmentation has wasted space in small chunks between allocations, internal fragmentation has wasted space within the allocations themselves.
A nice example would be an allocator that always gives out memory in equal-sized chunks of 100 MB. External fragmentation would not be a problem since all allocations are the same size, meaning there won't ever be any useless small holes between allocations. However, there will be massive internal fragmentation since many processes will only use a small fraction of their 100 MB allocations.
Memory allocation algorithms
Fragmentation of some sort or other is unavoidable. The best we can do is to try to minimize it. Let's look at a few common ways that memory allocators give out memory.
- First fit — In this scheme, the allocator starts at the beginning of memory and looks for the first available opening that is large enough to handle the request.
- Next fit — This is similar to first fit except that instead of always starting at the beginning of memory, it remembers where its last allocation finished and starts searching there. If it reaches the end, it wraps around to the start.
- Best fit — In this scheme, the memory allocator searches for the open space that most closely fits the request. In other words, it picks the smallest available space that works.
- Worst fit — This is the opposite of best fit in that the allocator always picks the largest available spot instead of the smallest.
Let's look at an example. Suppose memory looks like below and then we get the following sequence of allocations and deallocations: first, E requests 4 units, then F requests 15 units, finally G requests 5 units.

First fit
E requests 4: The first spot large enough is 10-13.
F requests 15: The first spot large enough is 50-64.
G requests 5: The first spot large enough now is right after E, at 14-19.

Next fit (assuming the last allocation was D, which runs from 75 to 94)
E requests 4: The search starts at 95, which is open, so we use 95-99.
F requests 15: The search starts at 99, but 99-100 is too small. So we start back at the beginning and find 50-64 is the first thing that works.
G requests 5: The last allocation was 50-64, so we start searching at 65 and find that 65-70 works.

Best fit
E requests 4: The smallest slot that fits is 95-99.
F requests 15: The smallest slot that fits is 50-64.
G requests 5: The smallest slot that fits is 10-14.

Worst fit
E requests 4: The biggest slot available is 50-54.
F requests 15: The biggest slot available is now 55-69.
G requests 5: Now that E and F are filling up most of the formerly empty slot from 50 to 74, the biggest open slot is 10-14.

These four methods are the basic ones that are standard in most operating systems texts. First fit is easy to implement and runs very quickly. Next fit helps spread out memory allocations so they are not all focused around the beginning, which is a drawback of first fit. This sort of thing can be helpful in certain applications. For instance, some types of memory, like the memory used in solid state drives, has a limit number of writes and rewrites before it burns out. Spreading out the wear helps prevent this.
Best fit is slower than first and next fit since it has to search for the smallest open slot. Worst fit seems like a silly thing to do, but there is a reason for it. Best fit tends to leave a lot of small holes in memory. For instance, if a request comes in for 9 units and we have a 10 unit free area from location 15 to 25, then when we allocate spots 15 to 24 for the request, the spot from 24 to 25 will likely be too small to be useful for anything else. But it also rapidly uses up large chunks.
All four methods above lead to large amounts of external fragmentation if run long enough. A different method, called quick fit, performs much better in real-world applications. The key insight here is that certain block sizes are requested a lot. So quick fit maintains certain areas that are already broken up into pieces of popular sizes, and it has another area for all other types of allocations, for which one of the algorithms above might be used.
Many real-life allocators are implemented using a linked-list approach. A small portion at the beginning of each free or used block is set aside for management of that block. It contains information on how large the block is, and it contains a pointer to the next block. A certain attack called a heap-based buffer overflow can be used to overwrite these informational areas with bogus data, allowing an attacker to access memory they wouldn't ordinarily be able to access.
Virtual memory
On the early computers of the 1940s and 1950s, and on the early PCS of the 1970s, processes had direct access to all the memory on the computer. The problem with this is that those processes could, either on purpose or by accident, read and write the memory of all other processes. This is not a good idea, so people developed ways to limit each process to its own chunk of memory. We'll talk about early approaches and then move on to paging, which is used by most modern systems.
The idea of virtual memory is that the operating system should be free to divvy up memory however it seems fit, and the process should not have to worry about exactly where in physical RAM it is located, if its memory is broken into non-contiguous pieces, where other processes' memories are, etc. The OS handles those details and allows the process to pretend that it has full access to all of RAM. This is why the memory is called “virtual.” It's just a pretend version that with the OS hiding all the messy details from the process.
To a process, the memory it is given looks like a continuous chunk of stuff starting at address 0. This is the process's address space. As mentioned above, the process's memory may be spread all throughout physical RAM, but the process doesn't have to worry about this. The OS takes care of it. .
For most systems, the address space's size is a power of 2. On modern systems, 32-bit and 64-bit address spaces are common. A 32-bit address space has addresses from 0 to 232–1, which is a little over 4 GB of space. Systems usually use hex to display addresses. In a 32-bit system, those addresses range from 00000000 to FFFFFFFF.
A 64-bit system has addresses that run from 0 to 264–1, which corresponds to over 18 exabytes (18,000,000,000 gigabytes) of memory. The addresses range from 0000000000000000 to FFFFFFFFFFFFFFFF, though most of that address space is out of reach due to it being so tremendously large.
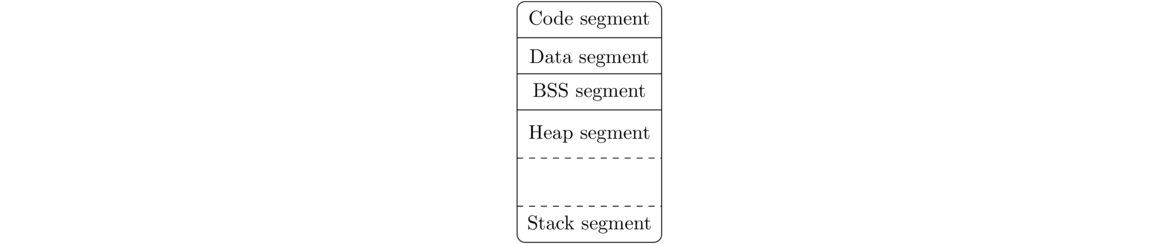
The address space is usually broken up into a few distinct pieces traditionally called segments. These are as follows:
- Code Segment — Sometimes called the text segment, this holds the program's machine language instructions.
- Data Segment — Also called the initialized data segment, this holds global variables for the process that have been assigned starting values.
- BSS Segment — Also called the uninitialized data segment, this holds global variables that were not assigned initial values.
- Heap Segment — This is an often large block of memory used for memory allocations while the program is running. When a C program uses malloc, this is where the allocated memory lives.
- Stack Segment — This is for data related to function calls. Each function call gets its own stack frame that holds the function's local variables, parameters, the return address of which instruction to run once the function is done, and a few other things.
The address space is usually laid out in the order shown below, with address 0 at the top. In between the heap and stack is empty space that they both expand into, with the heap growing down toward higher addresses and the stack growing up toward lower addresses. Usually, the heap is allowed to take up more space than the stack.
Here is a short C program to illustrate the different segments.
#include <stdio.h>
#include <stdlib.h>
int g = 5;
int main() {
int x = 3;
int *m = malloc(100*sizeof(int));
printf("address of main: %p\n", &main);
printf("address of g: %p\n", &g);
printf("address of m: %p\n", m);
printf("address of x: %p\n", &x);
}
Here is the output I got when running it. We see main, from the code segment is at the lowest address. Next comes the global variable g in the data segment, followed by the allocated memory on the heap. At the end is the local variable x, which is on the stack. Notice its address is right near the bottom of the address space.**The address is not all the way at the very bottom. It's closer to address 248–1 than address 264–1. See the section on the multilevel page table for why.
address of main: 0x4005e6 address of g: 0x60102c address of m: 0x6692a0 address of x: 0x7fff0b981174
Older approaches to memory management
This is one of the oldest approaches to memory management. Each process is given a certain region of RAM. Maybe A is given addresses 0 to 99, B is given addresses 100 to 199, C is given addresses 200 to 299, etc. The starting address for A is 0, for B is 100 and for C is 200. When each process is running, its starting RAM location is stored in a register called the base register. Whenever the process wants to access an address in its address space, the value in the base register is added to it to get the true address. For instance, in the example above B's address space runs from 0 to 199, and it is stored in physical RAM in addresses 100 to 199. If B wants to access address 12 in its address space, we add 100 to 12 to get 112 as the address in physical RAM.
In the simplest systems, there is only a base register, but in a true base and bounds approach, there is a bounds or limit register, which holds the upper limit of where the process's memory ends. If the result of adding the address and the base register exceeds this value, then the memory access is invalid and the process will likely be terminated by the OS. For instance, if process B tries to access address 350 of its address space, we would add the base value 100 to it to get 450, compare that with the bounds register, which is 199, and since 450 > 199, the memory access is invalid.
The base and bounds approach is not used much anymore. The problem is that it requires the process's entire address space be held in physical memory. On a 32-bit system, that address space is 4 GB in size, which wouldn't leave room for very many processes to be in memory. On a 64-bit system, it would be all but impossible.
For many processes, most of their address space is empty. In particular, there's usually a big hole between the heap and stack. The idea of segmentation is to break the process's address space into separate segments (code, stack, heap, etc.) and store each one in its own location in memory, typically using a base and bounds approach for each segment. This saves space and makes it easier for the OS to find a place to store the process's address space in memory since it's not all in one large chunk anymore. Segmentation was used on several systems in the past, including many Intel CPUs of the 1980s. Instead of segmentation, most modern systems use paging, covered in the next section.
Though segmentation isn't used much anymore, the term lives on in multiple places. One place you'll see it is if you make an invalid memory access in a C program. The error you'll see is called a segmentation fault. There's probably not any segmentation involved; the name is a holdover from the days of segmentation.
Paging
The system of virtual memory used in most modern operating systems is paging. In it, a process's address space is broken up into equal-sized units called pages. Physical RAM is broken up into equal-sized units called frames, which are the same size as pages. Each page of a process's address space is stored at a particular frame in physical RAM, and that frame can be anywhere. See below for an illustration.

In the illustration above, just one process's address space is shown. Some of the frames in physical RAM that aren't pointed to in the figure might be storing pages from other processes. Other frames might be free. The operating system uses a table, called a page table, to keep track of which pages correspond to which frames. The OS maintains a separate page table for each process. A simplified version of that page table might look like below. In reality, there is a little more information that is stored with each page besides the mapping.
| Page | Frame |
| 0 | 3 |
| 1 | 1 |
| 2 | 0 |
| 3 | 7 |
| 4 | 5 |
Pages are most often 4 KB (4096 bytes) in size. Because pages are generally all the same size, external fragmentation is not a problem. Keeping pages relatively small, at 4 KB, means there won't be too much internal fragmentation. Smaller page sizes would reduce internal fragmentation further, but that would also increase the size of the page table. It would lead to some inefficiencies due to the overhead of paging (which will be covered coming up).
In special cases, jumbo pages of a megabyte or even a gigabyte in size are possible. These are for programs where performance is critical, like databases or the OS kernel itself. Large pages are more efficient because they cut down on the overhead of paging.
Virtual addresses
Most systems will display addresses in hex. What's nice about hex is it's easy to convert hex addresses into binary. It's more painful to convert decimal into binary. For converting from hex, each hex digit will map to four binary bits according to the table below.
| 0 | 0 | 0000 | 4 | 4 | 0100 | 8 | 8 | 1000 | 12 | C | 1100 |
| 1 | 1 | 0001 | 5 | 5 | 0101 | 9 | 9 | 1001 | 13 | D | 1101 |
| 2 | 2 | 0010 | 6 | 6 | 0110 | 10 | A | 1010 | 14 | E | 1110 |
| 3 | 3 | 0011 | 7 | 7 | 0111 | 11 | B | 1011 | 15 | F | 1111 |
The addresses in an address space are broken up into two parts, one for the page and the rest for where in the page that address belongs, called its offset. Let's look at a small example. Suppose a system uses 8-bit addresses with the upper 3 bits of the address for the page number and the other 5 bits for the offset, like shown below.

With 8-bit addresses with 3 bits for the page and the other 5 for the offset, there are 28 = 256 possible addresses, 23 = 8 pages, and 25 = 32 offsets in each page. In other words, the 256 addresses in the address space are broken into 8 pages with 32 memory locations in each page. In this system, addresses will range from 00 to FF in hex.
To find the page number and offset for an address, first write it in binary. Suppose our address is B6 in hex. This becomes 10110110 in binary. Then we break it at bit 5 into 101 10110, with 101 giving us the page number and 10110 giving us the offset. In decimal, this is page number 5 and offset 22 into that page.
The above is how a human would do this calculation. Computers would do it differently, using bitwise operations. To get the page number, a computer would use a bit shift operation. For the example above, we want the upper three bits. We can get them by shifting the entire binary number over 5 slots to the right. This will turn 10110110 into 00000101, with the original 5 rightmost bits falling off the end and being replaced by zeros on the left. In most programming languages, the syntax for this is addr >> 5, where addr is the address.
To get the offset, a computer would use the bitwise AND. Specifically, we want an operation that zeroes out the upper 3 bits and leaves the other 5 bits untouched. This can be done by AND-ing with the binary value 00011111, which is 3 zeroes followed by 5 ones. This works because if you AND anything 0, you get 0, and if you AND anything with 1, it remains unchanged. In a programming language, we could do this by addr & 0b00011111. If you prefer hex, this becomes addr & 0x1F.
In general, if a system uses n bits to represent addresses with p of those for the page and the rest for the offset, the following two formulas will pull off the page number and offset.

Suppose we have the address 4EA2. In binary, it is 0100 1110 1010 0010. Grouping this into 5 bits for the page and 11 for the offset gives 01001 11010100010. In decimal, 01001 is 9, so this is page number 9. And in decimal, 11010100010 is 1698, so this is offset 1698. Using the bitwise formulas, we could get the page by doing 0x4EA2 >> 11 and we could get the offset by doing 0x4EA2 & 0b0000011111111111 or 0x4EA2 & 0x07FF.
0x before it. For instance 4EA2 becomes 0x4EA2. For binary, use 0b in place of 0x. Also, in Python, the built-in hex function can be used to convert a number to hexadecimal. For instance, hex(3456) converts 3456 to D80. The bin function converts to binary. To go the other way, if you print out the number prefaced with 0x or 0b, it will automatically write it in decimal. You can also use something like int('d80',16) or int('11101',2) if your number is a string.
More about paging
Fortunately, most processes only use a small fraction of their address space, meaning most pages are unused. The page table will have large runs of entries that aren't used. It's a waste to have entries for these in the page table. So a second level is added to the page table. This is sometimes called a page directory. The idea is we can divide the pages into groups. Each page group is an entry in the page directory. If all the pages in a group are not in use, then that group is marked to indicate that it's not in use, and we don't actually have a portion of the page table for that group. It's only if a page in a group is in use that we actually have a page table for that group.
Below is an example. On the left is a page table with the pages grouped into groups of 4. Each of those four groups becomes an entry in the page directory on the right. The page directory holds pointers to the groups (which are essentially mini page tables).

The 32-bit x86 architecture uses a two-level page table like this. However, with a 64-bit address space, the page directory itself is too large to fit into memory. So another level is added, which groups entries in the page directory in a similar way to how entries are grouped in the first level of the page table. In fact, most newer Intel CPUs use a four-level page table. Bits 0 to 11 are for the offset, 12-20 are for the page number, 21 to 29 are for the page directory entry, 30 to 38 are for the level 3 entry, 39 to 47 are for the level 4 entry, and the remaining bits are currently unused.
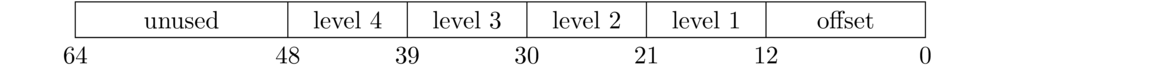
The fact that bits 48 to 63 are unused means that even though a 64-bit address space corresponds to a max of 264 ≈ 18 exabytes of space, because bits 48 to 63 are unused, the actual max is 248 ≈ 280 terabytes, though various other physical and financial limitations would keep you from being able to put that much RAM into a system.
The page table is stored in RAM. In a 64-bit system, looking up an entry in that table typically takes four separate memory accesses as we walk through the four levels of the multilevel page table. This means every memory access has a huge overhead. We would like to avoid this if possible. The solution is to remember the results of recent page table lookups to avoid having to do them again. Quite often, if we need a particular memory location, we will likely need it again in the near future, so it makes sense to store the results of the page table lookups. These are stored in a type of cache called a translation lookaside buffer (TLB).
The TLB is built in such a way that the all the entries can be checked simultaneously in parallel. This allows lookups to be done in just a few nanoseconds, much faster than the several hundred nanoseconds required to walk the page table. The cost of this, however, is that the TLB must be very small. A large TLB would take too long to search. Typical TLBs have from a few dozen to a few hundred entries. Because the TLB is so small, effort needs to be spent on deciding which entry to kick of the cache to make room for the new entry. We will cover algorithms for that later. Many modern systems have multiple TLBs.
When a context switch happens, many or most of the pages in the TLB may not be relevant to the new process. For this reason, the TLB is usually cleared out or flushed during a context switch. This also prevents the new process from having access to the old process's pages.
It's called a TLB miss when a page is needed but is not in the TLB. TLB misses cause a big performance loss since page table walks are so much slower. If you're a programmer and your code is running unexpectedly slow, it's possible that something in your algorithm is causing the TLB not to be used in an efficient way. It could also be that something about your algorithm is not making good use of the L1 and L2 caches. Chances are that the problem is something higher level than this, but the TLB and caches are something you should consider.
Regardless of the scheme, some hardware is needed to assist with memory accesses. This hardware is part of the CPU and is called the memory management unit (MMU). In the simple case of base and bounds, the MMU might only consist of registers to hold the base and limit values. With paging, the MMU has hardware to assist with reading the page table. The TLB is also part of the MMU.
Swapping
It's reasonable to ask why we even have RAM at all. Most computers nowadays have hundreds or thousands of gigs of hard drive space, so why not store everything on the hard drive? The reason is that hard drives are so much slower than RAM memory. An SSD is about 10 to 20 times slower than RAM and an HDD can be over a thousand times slower. But, we can use hard drive space to augment RAM. Things in RAM that are not currently being used can be stored out on the disk and brought back in when they are needed. This process is called swapping. A typical system with 4 GB of RAM might use 2 GB of swap space on disk. Because disk I/O is slow, we don't want to overuse swapping. We try to keep frequently used pages in RAM and use the swap space on the hard drive as an overflow, especially for things that haven't been used recently.
Summary of virtual memory in a modern system
A process's address space is divided into equal-sized chunks called pages. In many typical systems, pages are 4 KB in size, though a few special processes can have larger pages. Real physical RAM is broken up into equal-sized chunks called frames that are the same size as pages. The pages of the address space are mapped to specific frames in physical RAM.
The operating system maintains a page table for each process to keep track of which pages are mapped to which physical frames. That page table would have far to many entries to hold in memory, but since most of the process's address space consists of addresses that don't map to a real frame in RAM, a multilevel page table is used that doesn't need much memory to keep track of those empty spots in the address space.
Consulting the page table to find the physical location of an address is a slow process, so a cache called the TLB is used to remember the results of some of the previous page table lookups. In order to give the illusion of having more RAM than is actually available, operating systems use a little hard drive space to store pages that a process is not currently using. Care must be taken to keep as much of the process's working set in memory as possible. When a needed page is not in memory but is swapped out to disk, that's a page fault, which requires a slow disk read to bring the page back into memory.
It's worth going through the whole process of how a memory address is resolved. When the process wants to access an item in memory, the system first checks the CPU caches (L1, L2, and L3) for it. If it's not in the cache, then we need to find where it is in physical memory. To do this, the TLB is checked first. If the page to frame translation is not there (a TLB miss), then we walk the page table. If the page table indicates the page has been swapped out to disk (a page fault), then we have to read the page in from disk. Cache misses, TLB misses, and page faults each cause delays in accessing memory.